基于灰色Verhulst优化模型的装备研制费用高精度预测
2011-12-15刘光军柯宏发刘嘉文
刘光军,柯宏发,刘嘉文
(1.总装备部 通信网络管理中心,北京100720;2.装备学院,北京101416)
1 引言
武器装备全寿命周期费用技术受到了越来越广泛的重视[1,2],对武器装备系统研制费用进行预测,可为国防预算的节省,新武器装备系统的论证、研制、生产、使用和保障等全寿命管理提供可靠的依据[3]。针对装备研制费用预测问题,小样本问题和新型智能优化算法是目前的研究热点,如文献[2]将神经网络引入到灰色Verhulst模型来提高研制费用预测精度,文献[3]建立了基于粗糙集的RBF神经网络装备研制费用预测模型。从实际工程背景来看,装备研制遵循方案论证、初样设计研制、正样设计研制、靶场试验、定型等工作程序;大部分装备研制费用随着时间的推移,经费需求初期少,中期的某一时期达到高峰,后期又减少,研制费用累积曲线呈S型变化特征[4]。灰色Verhulst模型是一种很广泛的动态预测模型,是S型小样本数据列建模的有效工具,在军事装备研制费用预测领域取得了广泛的应用,如文献[4]利用灰色Verhulst模型对鱼雷研制费用进行了建模。
但是灰色Verhulst模型是有偏差的灰指数模型,在应用过程中存在模拟预测精度不高的情况,对其改进方法的研究也是灰色理论与应用研究的热点问题之一[5,6,7,8,9]。如文献[7]提出了以x(1)(n)作为初始条件的建模方法,文献[8]提出了以残差进行修正来提高灰色Verhulst模型的建模精度。
本文认为初始数据列系统是动态变化发展的,背景值的构造形式和初始条件的选取是相互影响的,考虑背景值优化和初始条件优化之间的误差积累传播,提出了基于数学规划的灰色Verhulst模型优化方法,介绍了应用模拟退火算法求解该模型。通过对模拟数据的比较分析发现,应用本文所提出的灰色Verhulst优化模型来对装备研制费用进行建模,比文献[4]、文献[8]有更高的模拟精度,并与原始数据列具有更大的灰关联度。
2 灰色Verhulst模型及其求解
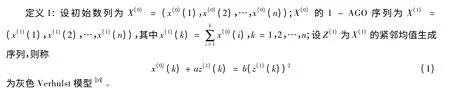
命题1(证明略):灰色Verhulst模型x(0)(k)+az(1)(k)=b(z(1)(k))2中待估计参数a为模型的发展系数,待估计参数b为模型的灰作用量,另设^a=(a,b)T为参数列,且设

在实际建模过程中,可以取初始序列为X(1),其1阶累减生成序列为X(0),建立灰色Verhulst模型直接对X(1)进行模拟。
3 灰色Verhulst优化模型
3.1 基于数学规划的灰色Verhulst优化模型
Verhulst模型主要用来描述非单调摆动发展或具有饱和状态的过程,即S形过程,最初慢慢上升,然后迅速增长,最后慢慢趋于极限,常用于人口预测、生物生长、繁殖预测和产品经济寿命预测等。建立灰色Verhulst模型的实质就是通过建模得到初始序列的拟合曲线,从拟合预测的角度出发,则希望最终的模拟序列能够最优地逼近初始序列,并且能具有较高的预测精度。由上节建模过程可以看出,模拟序列的建模精度取决于背景值逼近精度和初始条件常数c的精度。
定义1中Z(1)的紧邻均值生成是一种平滑处理,当时间间隔很小、序列数据变化平缓时,这样构造的背景值是合适的,模型偏差较小;但当序列数据变化急剧时,这样构造出来的背景值往往产生较大的滞后误差,模型偏差较大,因而在一定程度上会影响预测精度。另外,以数据表征的各种系统是动态变化的,因此以固定的背景值构造形式应用于所有系统也是不合适的。根据灰色系统的新信息有限原理,在进行背景值的构造时可以考虑新旧信息的相对重要性,本文采用下述背景值加权构造形式,即:
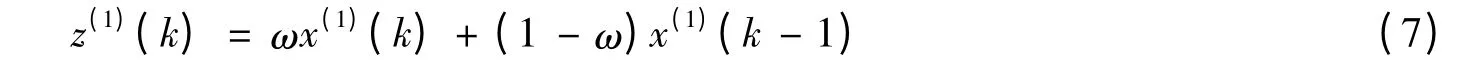
式(7)中,ω为新信息的加权权重,针对不同的系统进行优化求解。灰色Verhulst模型本身是一个模拟预测模型,如果以系统的当前预测点为原点,在该原点之前,越远离原点数据的信息意义将逐步降低,再进行Verhulst模型预测的意义就越弱,越靠近原点的数据信息更能反映系统的目前特征,所以在进行建模时考虑数据的相对重要性显然是合理的。
针对初始条件常数c的优化,强行令初始值为x(1)(1)来推导常数c缺乏严格的理论依据,使得解出的灰色Verhulst模型不一定是最佳预测公式;另外令初始值为x(1)(n)来推导常数c,由于x(1)(n)是由原始序列累加生成的,原始序列的信息通过x(1)(n)都可以得到充分反映,因此把它作为初始条件符合灰色系统理论新信息优先原理,也符合灰色系统理论最少信息原理,有可能使模型的预测精度比原模型的预测精度得到提高,但是不能保证与原始数据列保持最好的动态发展趋势。由上节建模过程可以看出,背景值的构造形式对常数c的求解是有影响的,也就是说,背景值优化带来的偏差会影响初始条件常数c优化。于是,基于背景值优化和初始条件优化之间的误差传播累积作用,针对任意的加权权值ω下,本文考虑模拟值与原始值的相对误差平方和最小的目标来优化确定常数c,其相对误差平方和ΔEω为:
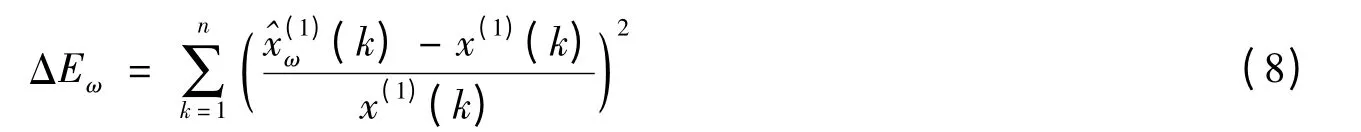
将c代入式(5),求得^x(1)(k),它是ω和c的函数。于是得到灰色Verhulst参数优化的数学规划模型:
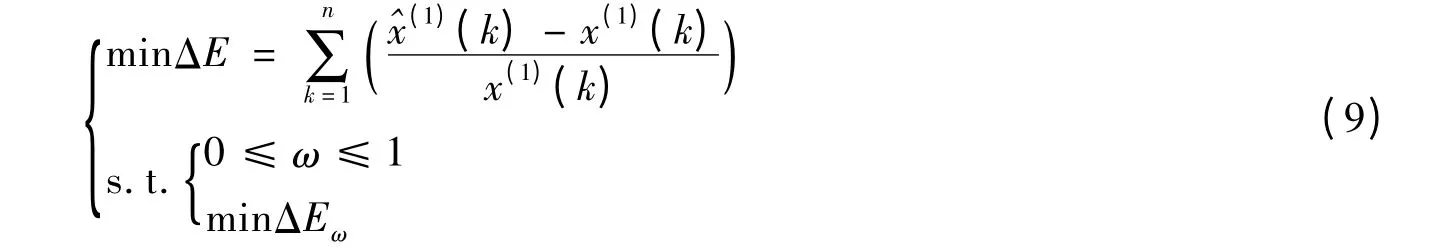
求解该模型得到最优的ω、发展系数a、灰作用量b和初始条件常数c,根据式(5)即可求得灰色Verhulst模型的最优模拟时间响应序列。该模型中ΔE和ΔEω都是非线性函数,本文选用模拟退火算法进行求解。
3.2 灰色Verhulst优化模型的模拟退火算法
模拟退火算法,就是模拟固体退火过程的一种组合优化算法,在求解过程中不但接受对目标函数改善的状态,而且还以某种概率接受使目标函数恶化的状态。算法由一个控制参数T决定,经过大量解变换后,可求得给定控制参数下优化问题的相对最优解;然后缓慢减小参数T的值,重复迭代过程,当参数T趋于0时,系统状态对应于优化问题的全局最优解。这种算法的特点可以使之避免过早收敛到某个局部极值点,从而能够比较有效地进行全局搜索最优值。
3.3 模型拟合的有效性分析方法
对灰色Verhulst模型进行优化的目的是使得最终的拟合曲线能够最优地逼近初始序列曲线,因此需要考察灰色Verhulst模型拟合的模拟序列与初始序列X(0)的接近性与相似性。灰色系统理论中灰色关联分析的实质就是比较数据到曲线几何形状的接近程度,一般来说,几何形状越接近,变化趋势也就越接近,灰关联度就越大。因此,本文利用模拟数据列与X(0)的灰色关联度大小来比较分析拟合的有效性,两者的灰色关联度越大,表示拟合曲线与系统曲线X(0)越接近,几何形状越相似,用序列来模拟序列X(0)越有效。
在进行灰关联分析时,以初始序列X(0)作为参考序列,然后求得各种模拟数据列与X(0)的灰色关联度,进而根据灰色关联度的大小进行判断即可。数据列与X(0)的灰色关联度用γ(,X)表示,有算式:
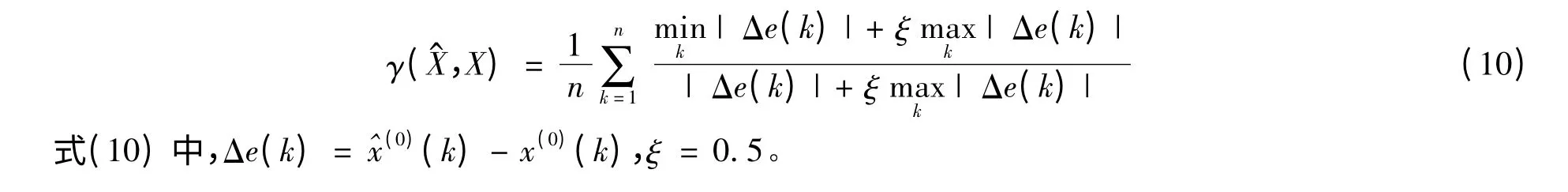
4 鱼雷研制费用算例验证
以文献[4]提供的鱼雷研制费用数据为例进行灰色Verhulst优化模型建模,鱼雷逐年研制费用和累积研制费用见表1。

表1 鱼雷逐年和累积研制费用(万元)
应用本文灰色Verhulst优化模型,求得最优的ω=0.4,其模拟时间响应式为:
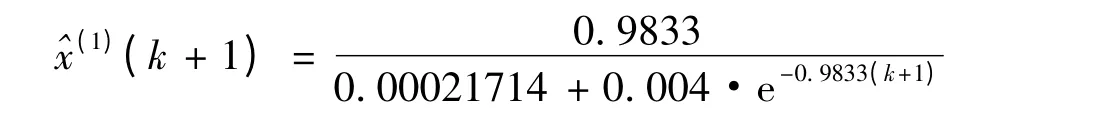
将该模型模拟结果和文献[4]、文献[8]的模型进行比较与分析。分别计算各模型的模拟数据,并将相应的实际数据、模拟数据、相对误差和平均相对误差列于表2。
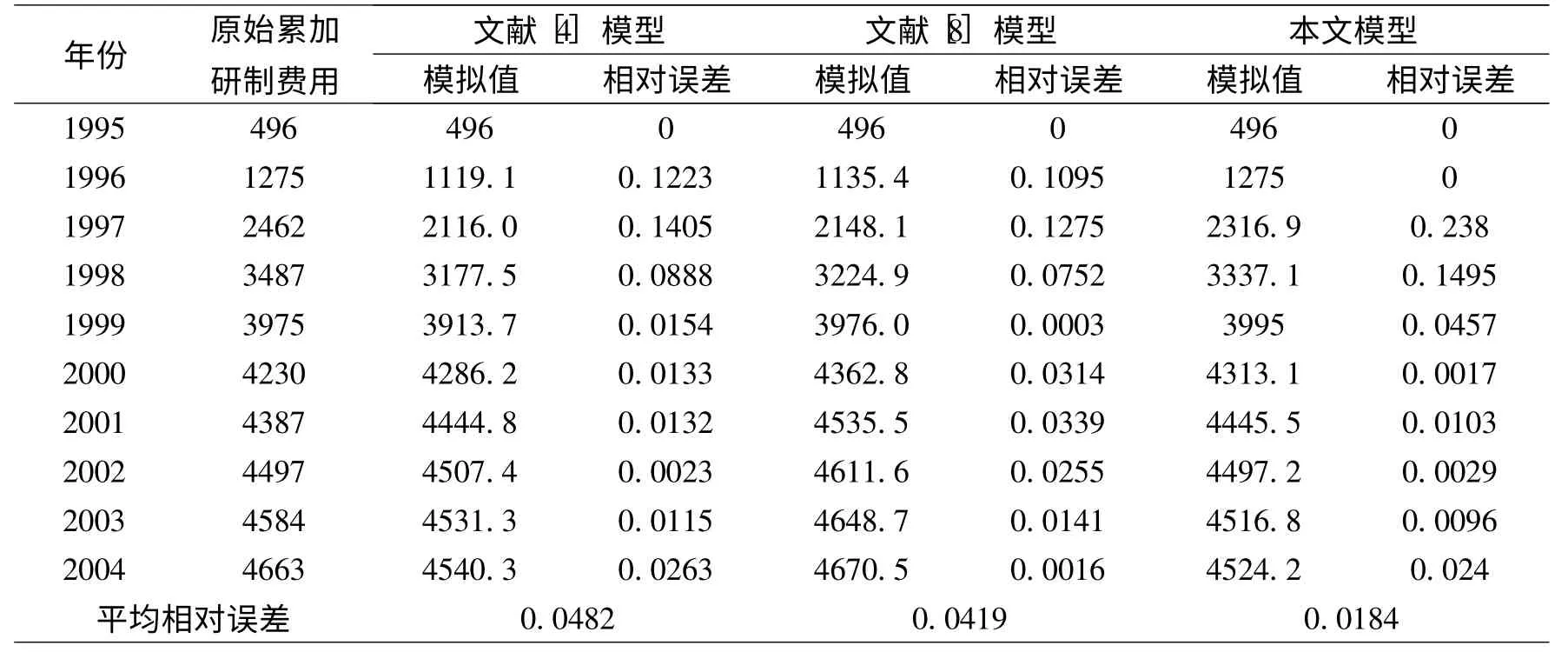
表2 各种模型的模拟精度比较
由表2可以看出,本文提出的灰色Verhulst优化模型的平均相对误差最小。假设X(0)代表原始数据列,分别代表文献[4]模型、文献[8]模型和本文模型的模拟数据列,各数据列曲线如图1所示。图中以虚线表示原始数据列,很直观地就可以看出,本文灰色Verhulst优化模型所得的模拟序列与原始序列的接近性与相似性最好,其模拟性能最优。
考察上述三种模型所得的模拟数据列与原始序列X(0)的灰关联度,基于式(10)求得=0.6755、γ(=0.6692和γ=0.7673,本文灰色Verhulst优化模型所得的模拟序列与原始序列的灰关联度最大,模拟预测性能最优。

5 结束语
装备研制费用的预测是武器装备全寿命管理中一项很重要的工作,本文提出了基于数学规划的灰色Verhulst优化模型,有效地解决了小样本装备研制费用预测问题,并且较好地提高了预测精度。大量数据仿真结果表明,本文所提模型也适用于其它呈S型特征的数据列预测问题。针对多峰值的研制费用预测问题[2,4],基于本文模型如何实现高精度预测值得进一步研究。
1 郭继周,宋贵宝,彭绍雄.装备使用保障费用灰色建模分析[J].系统工程与电子技术,2004,26(1):64-67.
2 刘建永,李凌,伍中军.基于神经网络灰色Verhulst算法的装备研制费用预测模型[J].解放军理工大学学报(自然科学版),2008,(4):335-338.
3 孟科,张恒喜,李登科,等.基于粗糙集的RBF神经网络在装备研制费用预测中的应用[J].装备指挥技术学院学报,2006,17(5):14-17.
4 梁庆卫,宋保维,贾越.鱼雷研制费用的灰色Verhulst模型[J].系统仿真学报,2005,17(2):257-258.
5 ZHAO ZHONGMING,CHEN XIEN.Surface Movement and Deformation Simulated by Verhulst Model[C]//Proceedings of 2009 2nd IEEE International Conference on Computer Science and Information Technology,Beijing,2009:459-461.
6 ZHAO WENQING,ZHU YONGLI.A Prediction Model for Dissolved Gas in Transformer Oil based on Improved Verhulst Grey Theory[C]//2008 3rd IEEE Conference on Industrial Electronics and Applications,Singapore,2008:2042-2044.
7 LUO YOUXIN,CHEN MIANYUN,CHE XIAOYI,et al.Non-equal Interval Direct Optimizing Verhulst Model that x(n)be Taken as Initial Value and its Application[J].Journal of Southeast University(English Edition),2008,24(Sup):17-21.
8 左燕.基于GM(1,1)改进的Verhulst模型预测PTA期货价格[J].周口师范学院学报,2009,26(5):38-40.
9 何文章,吴爱弟.估计Verhulst模型中参数的线性规划方法及应用[J].系统工程理论与实践,2006,26(8):141-144.
10 刘思峰,党耀国,方志耕.灰色系统理论及其应用[M].北京:科学出版社,2004.
