一种力位置控制冲击问题解决方法

肖金壮，熊鹏，李晓燕，王洪瑞

（河北大学电子信息工程学院，河北保定 071002）

一种力位置控制冲击问题解决方法

肖金壮，熊鹏，李晓燕，王洪瑞

（河北大学电子信息工程学院，河北保定 071002）

针对数控系统力位置控制过程中的力冲击问题，基于阻抗控制基本原理，研究了一种解决该问题的控制策略.以X－Y－Z三轴运动平台为被控对象，建立了系统数学模型以及力传感器动态数学模型.以控制Z轴与工件的恒定接触力为目标，构建了切换控制系统，并证明了闭环系统的稳定性.在Simulink中搭建了力位置双闭环阻抗控制仿真系统，结果证明了所设计策略能够针对随机厚度的加工件，实现恒定接触力的控制要求.

恒力控制；力冲击；阻抗控制；X－Y－Z三轴运动平台

力位置控制分为直接力位置控制和柔顺控制.柔顺控制是指控制器对外界施加的作用力干扰在一定程度上顺应或依从，以一定的位置偏差为代价来满足力控制的要求.与直接力位置控制相比，这种柔顺控制更具优势［1－2］.从使被控对象实现柔顺运动的控制方法考虑，大致可以分为2类：一是同时地分别控制力和位置，使二者之间不发生冲突，利用力和位置的正交原理，将被控对象的运动在笛卡尔坐标下分解，自由方向上的运动由位置控制方式去控制，受限方向上的运动由力控制方式去控制.此控制方法的代表是力位置混合控制，对此方法的研究无论是控制算法还是实现方法上都比较成熟，应用也很广泛［3］.二是通过建立位置偏差与被控对象所受到的外界力的关系来间接控制被控对象与外界环境之间的作用力.这一类控制方法的代表是阻抗控制.

针对力位置控制的研究内容，大体分为位置伺服、力传感器、机械臂末端约束条件和冲击下系统稳定性4个部分.对于机械臂末端约束条件的研究，无论是静态的约束条件还是动态的约束条件已经取得了较多的成果［4－7］.随着力位置控制在实际中的广泛应用［8］，机器人与外部环境的碰撞问题，即力冲击问题显得尤为重要.学者们通过气动人工肌肉［9］、改进型PD控制器［10］等方法有效避免了力冲击.本文以X－Y－Z三轴精密运动平台为控制对象，首先建立被控对象的数学模型，然后为了提高控制精度对传感器进行模型辨识，最后针对阻抗控制研究了一种避免力冲击，并且具有可靠稳定性的控制策略，为阻抗控制提供了一种实现方法，真实地模拟了此运动平台的操作情况.

1 系统数学建模

本文以X－Y－Z三轴运动平台为控制对象，构建了一种基于Simulink软件的仿真系统.首先设计位置闭环控制实现对X－Y平台和Z轴平台的位置控制，然后设计力闭环控制实现对Z轴平台的力控制，最后采用阻抗控制的形式实现力位置控制.控制结构简图如图1所示.

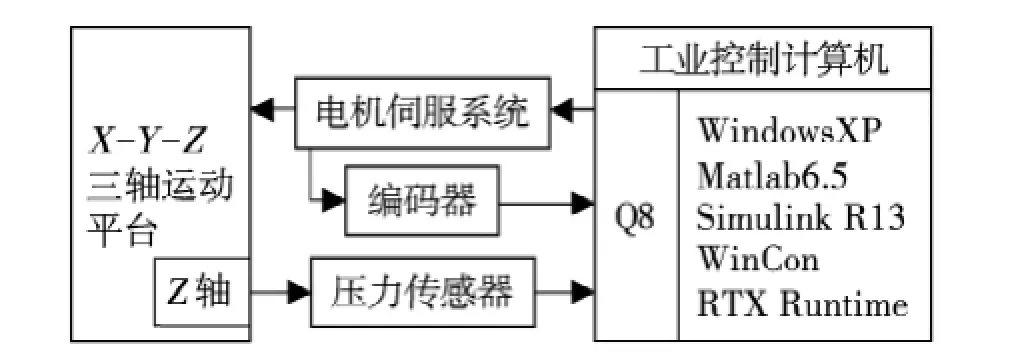
图1 控制系统构成Fig.1 Structure of the control system

1.1 伺服系统模型

考虑到电机承载能力的需要，系统中采用了2种类型的Panasonic A Series伺服电机，其中X和Y轴选用1 k W中惯量电机，Z轴选用400 W小惯量电机，供电均为单相交流220 V.伺服系统工作于速度控制模式，每套伺服系统输出±10 V的模拟控制信号用以对电机转速±5 000 r／min的连续控制.电机的转角通过2 500 p／r的旋转编码器反馈到控制器，经过电机驱动装置4倍频后产生104p／r的信号.丝杠通过联轴器与电机转子直连，螺距为5 mm，通过电机转动带动丝杠从而驱动滑块运动.由于采用的是滚珠丝杠传输，不失一般性的，本模型建立忽略丝杠和螺母间隙带来的定位误差.这样便构成了以控制电压u（t）为输入（单位：V），平台位移x（t）为输出（单位：mm）的单轴对象.

对象数学模型为

式中，U（s）和X（s）分别为u（t）和x（t）的零初始条件下的Laplace变换.

1.2 力传感器动态数学模型

本系统采用应变式拉压力传感器实时测量Z轴与滑块之间的接触力，传感器与一个形变系数为5 N／mm的弹簧连接，以提高系统的柔性度，同时为了避免传感器受过载而损坏，还设计有相应的支架，当弹簧形变超过50 mm时由支架承受过多的压力.

采用了最小二乘法来辨识压力传感器的动态数学模型［11－12］.压力传感器是二阶系统，其输入为位置变量，输出为力变量，所以建立频域模型为

首先对上式进行离散化.将s＝2／T（z－1）／（z＋1）代入，整理得

连续模型离散化后的形式为

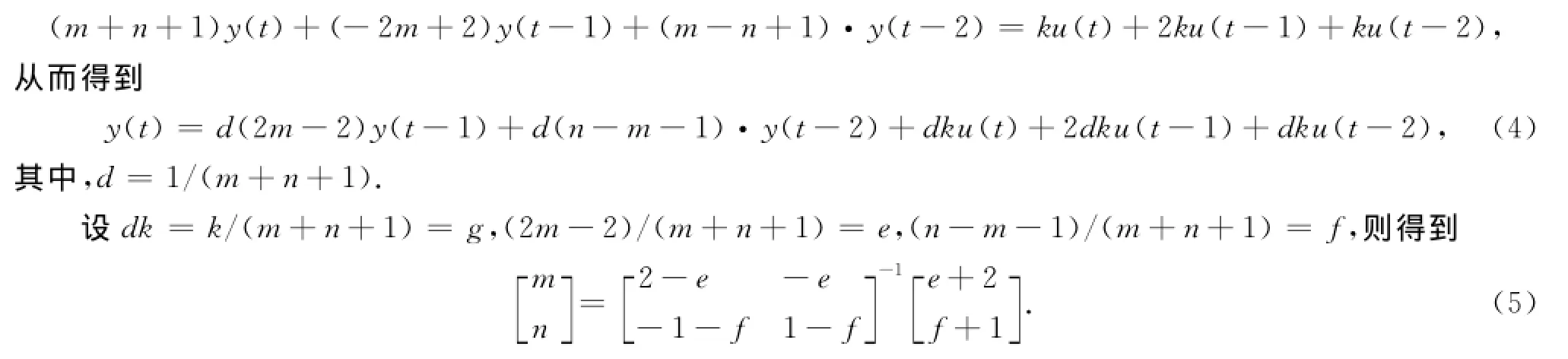
基于此模型，需要采集1组力、位置数据来确定参数［e，f，g］，从而确定模型（2）中的未知参数.首先给定Z轴的位置轨迹，使其位置的运动为正弦函数.Z轴在与滑动平台接触的过程中，传感器的输出信号随之变化.Matlab实时记录下位置和力的信号，并依据这些数据计算出力传感器的传递函数为

其中，P（s）和F（s）分别为输入位移和输出力的时间函数的Laplace变换.

利用同种方法测得另1组力、位置数据来检测所建模型.经计算，平均误差为－0.016 4，可以确定所建模型足够准确，可以应用.

2 控制策略和稳定性分析

系统整体的控制要求是在Z轴方向上给X－Y平台上的工件施加一个给定的力.本系统采用力位置双闭环模式的阻抗控制.位置环采用PD控制器，力环采用PI控制器，能有效地弥补PD控制器不能消除系统稳态误差的缺陷.

第1阶段：位置控制.系统给定为指定位置（X－Y平台），当输出位置与一随机扰动信号（加工件厚度）相叠加为给定位置时，传感器与平台上的加工件相接触产生接触力，从而位置控制结束进入力位置控制阶段.

采用PD控制器，根据之前的数学建模可知由控制器和被控对象组成的闭环控制系统为一阶系统.系统框图如图2所示.其中G1（s）为伺服系统的数学模型，H1（s）为PD控制器的数学模型.根据系统框图可以得到系统的动态响应方程，其动态矩阵的特征方程的根为x＝－2.04＜0，所以第1阶段系统稳定.

第2阶段：力位置控制.系统给定为指定力，输出位置经传感器模型后反馈到力控制的输入，利用位置的偏差与经过传感器得到的力信号之间的关系，通过控制位置最终达到力控制的目的.

采用PI控制器，根据之前传感器的系统辨识可知由控制器、被控对象和传感器模型组成的双闭环控制系统为四阶系统.系统框图如图3所示.

图2 位置控制系统框图Fig.2 Block diagram of the position control system

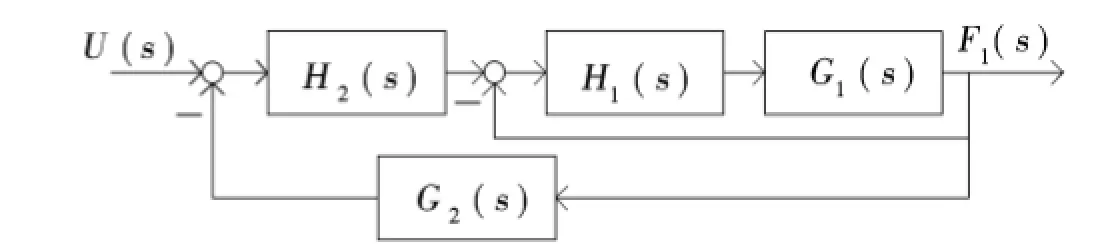
图3 力位置控制系统框图Fig.3 Block diagram of the force position control’s system

其中H2（s）为PD控制器的数学模型，G2（s）为传感器的数学模型.根据所得系统开环传递函数得到相角稳定裕量r＝130°＞0，所以第2阶段稳定.

第1阶段与第2阶段之间不存在耦合关系，所以闭环系统是稳定的.

3 系统仿真

基于前述建立的系统数学模型，利用Simulink功能模块建立系统的仿真模型.根据上述的控制思路，建立了如图4所示的Simulink仿真图.

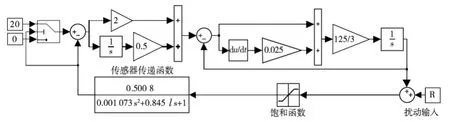
图4 系统Simulink仿真模型Fig.4 Simulink simulation model of the system

切换控制系统分为力控制回路和位置控制回路.其中，力控制回路的输出为位置控制回路的给定.

位置控制回路：给定输入为力控制回路的输出信号，负反馈为当前的位置信号；力控制回路：给定输入为20 N（给定力）的阶跃信号，负反馈信号是由传感器模型输出的力信号.传感器模型是经过系统辨识出的数学模型.

为完成第1子系统的单独位置控制，特别在力控制环的给定端加入了Switch模块，位置输出端加入了随机扰动信号R（加工件厚度），传感器模型输入端加入了Saturation模块.为方便说明控制过程，现设定XY平台接触面为Z轴的原点.平台上方为负半轴，下方为正半轴.平台上加工件厚度为随机数R.

第1子系统：当机械臂由Z轴负半轴开始运动到与平台上的加工件相接触这一过程中没有接触力，所以力控制环不起作用，位置控制环的给定应为零（Z轴原点）.为了保证这一点，Saturation模块的下限值为零.由于此阶段机械臂未接触X－Y平台上的加工件，所以输出位置与随机数R代数和为负值，经过Saturation模块使得在此阶段传感器模型的输入端为零，力控制环的反馈为零；Switch模块的选择条件为大于零，也就是说，此阶段由于传感器模型输出的数值一直等于零，从而力控制环的给定为零.这样就能保证位置控制环的给定为零.

第2子系统：当位置环输出与随机数R的代数和大于等于0之后，Saturation模块输出此时真实的位置，经过传感器模块反馈到力控制环；Switch模块中，由于选择信号的输入大于设定值从而输出20 N，即幅值为20的阶跃信号作为力控制环的给定.这样便进入了阻抗控制过程.

切换控制系统在R＝5和R＝10时的MATLAB仿真结果分别如图5，6所示.

图5 R＝5情况下仿真结果Fig.5 Simulation result with R＝5

图6 R＝10情况下仿真结果 Fig.6 Simulation result with R＝10

图5，6中，实线为力的给定值曲线，虚线为力的测量值曲线，可以看出R在随机取值的情况下，切换系统都能满足恒定接触力的控制要求.

4 结论

通过将切换控制思想引入数控系统力控制过程中，设计了相应的力控制策略，并证明了闭环系统的稳定性，基于所构建的以X－Y－Z三轴精密运动平台为控制对象的半实物力控制仿真系统，对所设计力位置控制方法的有效性进行了验证.结果表明：首先，将系统中反馈部分力传感器的输出作为选择信号，在不同控制阶段选择系统不同的给定输入，可以实现在不同子系统之间的切换控制；其次，切换思想的引入，可有效地解决单纯位置控制与力位置控制之间的冲突，即力冲击问题，提高了运动系统与环境力接触过程中的柔性；最后，该方法实现过程简单，特别适于现代数控系统的力位置控制改造与应用.

［1］ZUEV A V，FILARETOV V F.Features of designing combined force／position manipulator control systems［J］.International Journal of Computer and Systems Sciences，2009，48（1）：146－154.

［2］HU Y，GEORGE V.Position and force control of flexible joint robots during constrained motion tasks［J］.Mechanism and Machine Theory，2001，36（7）：853－871.

［3］FUSAOMI N，TETSUO H，ZENKU H.A desktop NC machine tool with a position／force controller using a fine－velocity pulse converter［J］.Mechatronics，2009，19（5）：671－679.

［4］黄绍辉，曹小涛，李元春.基于小波神经网络的机械臂力／位置控制算法［J］.吉林大学学报：工学版，2008，38（1）：163－167.

［5］周芳，朱齐丹，姜迈，等.受限机械臂的自适应小波滑模位置／力混合控制［J］.华中科技大学学报：自然科学版，2009，37（11）：9－12.

［6］FAROOQ M，WANG D.Hybrid force／position control scheme for flexible joint robot with friction between the end－effector and the environment［J］.International Journal of Engineering Science，2008，46（12）：1266－1278.

［7］KARAYIANNIDIS Y，ROVITHAKIS G，DOULGERI Z.Force／position tracking for a robotic manipulator in compliant contact with a surface using neuro－adaptive control［J］.Automatica，2007，43（7）：1281－1288.

［8］TORGNY B.Present and future robot control development－an industrial perspective［J］.Annual Reviews in Control，2007，31（1）：69－79.

［9］范伟，彭光正，高建英，等.气动人工肌肉驱动球面并联机器人的力控制研究［J］.机器人，2004，26（4）：336－341.

［10］LIU Shengping，WU Licheng，LU Zhen.Impact dynamics and control of a flexible dual－arm space robot capturing an object［J］.Applied Mathematics and Computation，2007，185（2）：1149－1159.

［11］马勤弟，雷敏.薄膜热电偶的动态校准及辨识建模［J］.仪器仪表学报，1999，20（3）：300－302.

［12］张勇，杨慧中.有色噪声干扰输出误差系统的偏差补偿递推最小二乘辨识方法［J］.自动化学报，2007，33（10）：1053－1060.

A Solution for Impact Problem of Force Position Control

XIAO Jin－zhuang，XIONG Peng，LI Xiao－yan，WANG Hong－rui
（College of Electronic and Information Engineering，Hebei University，Baoding 071002，China）

A control strategy，which is based on the studying of the impedance control’s basic principles，is to solve the problem of impact force in the process of force position control in numerical control systems.X－Y－Zthree－axial motion platform was treated as the control object.The systemic mathematical model and the dynamic mathematical model of the force sensor were established.To control the constant contact force betweenZ－axis and workpiece，a switching control system was builded，and the stability of the closed－loop system was proven.The impedance controller with the position loop and the force loop were designed in the simulink software.The results validate that the designed strategy can achieve the constant contact force control requirements for the random thickness of workpiece.

constant force control；impact force；impedance control；X－Y－Zthree－axis platform

TP 273

A

1000－1565（2011）03－0309－05

2010－06－01

河北省自然科学基金资助项目（F2007000223）

肖金壮（1976－），男，河北定州人，河北大学讲师，主要从事机器人控制相关研究.E－mail：robot＠hbu.edu.cn

熊鹏（1986－），女，河北保定人，河北大学在读硕士研究生，主要从事机器人控制相关研究.

E－mail：xiong.peng＠hotmail.com

孟素兰）