一类推广的IMBq方程解的爆破

刘洋，赵军生，于涛

（1.西北民族大学数学与计算机科学学院，甘肃兰州 730124；2.黑龙江大学数学科学学院，黑龙江哈尔滨 150080；3.哈尔滨工程大学理学院，黑龙江哈尔滨 150001）

一类推广的IMBq方程解的爆破

刘洋1，赵军生2，于涛3

（1.西北民族大学数学与计算机科学学院，甘肃兰州 730124；2.黑龙江大学数学科学学院，黑龙江哈尔滨 150080；3.哈尔滨工程大学理学院，黑龙江哈尔滨 150001）

对一类推广的IMBq方程的初边值问题进行了研究，在非线性项满足一定条件的情况下，采用特征函数法和凸性方法，证明了问题的光滑解只能在时间的一个有界区间中存在，并且在有限时间T内爆破，即解于有限时间T内在某种意义下趋于无穷大，从而说明了这类典型的非线性发展方程解的奇性.

IMBq方程；初边值问题；特征函数法；凸性方法；爆破

MSC 2010：35K61

1 预备知识

1872年，Boussinesq提出了描述浅水波运动的方程称为Boussinesq方程（简称Bq方程）［1－2］.其中a是不为0的常数，当b＜0时，方程（1）称为好的Bq方程，用于模拟非线性弦振动和不变矩形槽内无黏性液体的二维无旋运动［3－4］；当b＞0时，方程（1）称为坏的Bq方程，用于描述在水平底面的浅水中，水波振幅较小时的二维流体的运动，也常用于大范围的物理现象的描述，包括离子声波在不变的同向等离子体中的传播和FPU问题中非调和点阵动力学［1，4－5］.

由方程（1）改进的如下方程utt－u xx－uxxtt＝（u2）xx称为IBq方程，该方程是在正合流体动力学方程组中提出的，用于描述与磁场成直角的波的传播，接近于坏的Bq方程［5］.修正的IBq方程模拟修正的Kd V方程产生的如下方程utt－Δu－Δutt＝Δ（u3）称为IMBq方程，常用于研究非调和点阵的性质和非线性Alfven波的传播［5］.对于Bq方程，IBq方程和IMBq方程，已有许多结果［6－13］.文献［14］研究了具有表面张力的水波问题时提出了模型方程utt－uxx－uxxtt＋au xxxx＋uxxxxtt＝（u2）xx，0＜x＜1，0＜t＜T，其中u（x，t）是未知函数，a＞0是常数，属于Bq方程.文献［15］对其广义解的存在性、唯一性和解的爆破进行了研究.文献［16］研究了具有零表面张力时的情形.文献［17－18］对非线性波动方程和拟抛物型方程解的爆破进行了研究.

但是，对于形如（2）的IMBq方程解的研究结果却很少.

其中u（x，t）表示未知函数，f（s）是给定的非线性函数，Ω⊂Rn是适当光滑的有界域，Δ表示在Rn中的拉普拉斯算子.

2 主要结果

文献［19－22］利用特征函数法和凸性方法研究了拟抛物方程整体解的不存在性与有限时间爆破，对于与抛物型方程完全不同的IMBq方程（2），研究了其初边值问题，初边值条件为

其中u0（x）和u1（x）分别为给定的初值函数.

引理1 （Jessen不等式）设g（x）定义在（a，b）上，g（x）∈［a1，b1］，其中a，b，a1，b1为有限数或∞，f（x）是（a1，b1）上的连续凸函数，q（x）∈L2［a，b］，且q（x）≥0，则有

在右端有限时成立.

定理1 设u（x，t）是问题（2），（3），（4）的解，且

又由格林第2公式

3 结论

本文在对非线性项施加增长限制的条件下，采用特征函数法和凸性方法证明了问题（2），（3），（4）的解在一个有限时间T内发生爆破，即解于有限时间T内在某种意义下趋于无穷大，

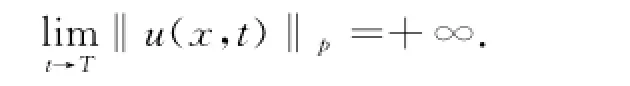
该结论说明了这类典型的非线性发展方程解的奇性，并且也为该类方程数值解的进一步研究提供了一定的参考.

［1］BERRYMAN J.Stability of solitary waves in shallow water［J］.Phys Fluids，1976，19：771－777.

［2］BOUSSINESQ J.Theotie des ondes et des ramous qui se propagent le long d’un cana rectangulari－re horizontal，en comuniquant au liquid contene dans ce canal des vitesses sunsiblement parielles de la surface au fond［J］.Math Pures Appl Ser，1872，2（17）：55－108.

［3］BONA J，SMITH R.A Model for the two－way propagation of water waves in a channel［J］.Math Proc Cambridge Philos Soc，1976，79：167－182.

［4］LINARES F.Global existence of small solutions for a generalized Boussinesq equation［J］.Differential Equation，1993，106：257－293.

［5］MAKHANKOV V.Dynamics of classical solution［J］.Phys REV Lett，1978，35（c）：1－128.

［6］FAN Y，GRILLAKIS M.Existence and uniqueness for Boussinesq type equation on a circle［J］.Comm Part Diff Eq，1996，34：1253－1277.

［7］LIN YUE.Decay and scattering of small solution of a generalized Boussinesq equation［J］.J Fuct Anal，1997，147：51－68.

［8］AKMEL DE GODEFROY.Blow up of a generalized Boussinesq equation［J］.IMA J Appl Math，1998，60：123－138.

［9］CHEN Guowang，WANG shubin.Existence and nonexistence of global solutions for the generalized IMBq equation［J］.Nonlinear Analysis TMA，1999，36：961－980.

［10］YANG Zhijian.Existence and nonexistence of global solution to a generalized modification of the improved Boussinesq equation［J］.Math Meth Appl Sci，1998，21：1467－1477.

［11］KALANTAROV V，LADYZHENSKAYA O.Occurrence of blow－up for quasilinear partial differential equations of parabolic and hyperbolic types［J］.Zap Nauk Som Lomi，1997，69：77－102.

［12］SACHS R L.On the blow－up of certain solutions of the“good”Boussinesq equation［J］.Appl Anal，1990，36：145－152.

［13］YANG Zhijian，CHEN Guowang.Blow－up of solutions for a class of generalized Boussinesq equation［J］.Acta Math Sci，1996，16：31－40.

［14］SCHNEIDER G，EUGENE C.Kawahara dynamics in dispersive media［J］.Physical D，2001，152－153：384－394.

［15］王艳萍.一类高阶非线性波动方程解的存在性［J］.数学的实践与认识，2004，34（10）：153－158.

［16］SCHNEIDER G.The long wave limit for a Boussinesq equation［J］.SIAM J Appl Math，1998，58：1237－1245.

［17］GLASSEY R T.Blow－up theorem for nonlinear wave equations［J］.Math Z，1973，132：182－203.

［18］张海亮，贾新春.具非线性边界条件的拟线性抛物型方程解的Blow－up［J］.Math，2002，22：195－198.

［19］徐润章，于涛.一类推广了的非线性发展方程解的爆破［J］.哈尔滨工程大学学报，2004，25（6）：818－821.

［20］徐润章，刘亚成.两类非线性拟抛物方程解的有限时间爆破和长时间行为［J］.工程数学学报，2005，22（5）：800－806.

［21］于涛，徐润章.一类非线性发展方程解的爆破［J］.哈尔滨工程大学学报，2006，27（4）：614－616.

［22］刘洋，赵军生，丁云华.一类半线性Schrödinger方程整体弱解的存在性［J］.黑龙江大学自然科学学报，2011，8（2）：210－212.

Blow－up of Solutions for a Class of Generalized IMBq Equations

LIU Yang1，ZHAO Jun－sheng2，YU Tao3
（1.College of Mathematics and Computer Science，Northwest University for Nationalities，Lanzhou 730124，China；2.School of Mathematical Science，Heilongjiang University，Harbin 150080，China；3.College of Science，Harbin Engineering University，Harbin 150001，China）

The initial boundary value problem of solutions for a class of generalized IMBq equations is studied.In the case of the nonlinear term satisfying some conditions，it is proved by using the eigenfunction method and convexity method that smooth solutions of the problem only exist in a bounded time interval and blow up in the finite timeT，that is，the solutions tend to infinity in the finite timeTin a sense.Consequently，the conclusion of this paper indicates the singularity of solutions for this typical nonlinear evolution equations.

IMBq equations；initial boundary value problem；eigenfunction method；convexity method；blow－up

O 175.26

A

1000－1565（2011）03－0240－04

2010－09－13

国家自然科学基金资助项目（10871055）

刘洋（1983－），男，黑龙江望奎人，西北民族大学助教，主要从事偏微分方程理论方面的研究.E－mail：xuezhongjing7890＠yahoo.com.cn

王兰英）