一类加权对称方程对称周期解的稠密分布

何涛，丁卫

（1.南通航运职业技术学院基础教学部，江苏南通 226010；2.南通大学理学院，江苏南通 226007）

一类加权对称方程对称周期解的稠密分布

何涛1，丁卫2

（1.南通航运职业技术学院基础教学部，江苏南通 226010；2.南通大学理学院，江苏南通 226007）

考虑一类带正权的次二次位势对称方程的对称周期解的分布问题，利用相平面分析法，证明了在一定条件下对称周期解是稠密分布的.

次二次位势；Hamilton函数；对称周期解；稠密分布

MSC 2010：34C25

考虑哈密顿系统

对称周期解的分布情况，其中a，p是连续的2π周期函数，g是连续函数.对方程（1）的周期解的研究已经有许多成果［1－3］.然而，当摄动项p（t）是对称函数时，关于对称周期解分布情况的结果并不多［4－5］.文献［4］中，Nakajima研究了Duffing方程

得到了在超线性条件下对称次调和解的稠密性分布结果.钱定边［5］在跨共振点的情况下也证明了类似的结果.而当方程满足次线性条件时，在研究过程中往往要通过变量代换［6－8］，方程的对称结构就遭到破坏，给对称周期解的研究带来了相当大的困难.

1 预备知识

采用直接的方法在条件

及次二次位势条件

在上述条件下，方程（1）的解是全局存在的［7］.方程（1）的等价方程为

定理1 设条件（g0），（G0）成立，a（t）是正的偶函数，g满足局部Lipschitz条件.若p（t）为偶函数（p（t），g（t）均为奇函数），则方程（1）存在一列偶（奇）次调和解｛x k（t）｝，满足

类似于文献［4］中的方法，利用对称条件，把周期解的问题转化为二点边值问题，通过对方程的解在相平面上定性行为的分析，可进一步得到下列结果.

定理2 若定理1的条件成立，则

1）若p（t）为偶函数，则对任意2个偶的次调的解x1（t）和x2（t）（x1（0）＝a1＜x2（0）＝a2，x1′（0）＝x2′（0）＝0），方程（1）存在无穷多的偶的次调和解˜x k（t），满足

2）若p（t），g（x）均为奇函数，则对任意2个奇次调和解x1（t）和x2（t）（x1（0）＝x2（0）＝0，x1′（0）＝a1＜x2′（0）＝a2），方程（1）存在无穷多的奇次调和解˜x k（t），满足

2 引理

在x2＋y2＞0时，方程（3）的极坐标形式为

记z（t；t0，z0）＝（x（t；t0，z0），y（t；t0，z0））为方程（3）在t0时刻从点z0＝（x（t0），y（t0））出发的解z（t），对应在极坐标方程（4）下的解为（r（t），θ（t））.

引理1［7］如果条件（g0）成立，则存在r0＞0，当r（t）＞r0时，θ′（t）＜0.

引理2［7］如果条件（g0）成立，则对任意正整数k，存在Rk＞r0及严格递增函数ζk∶［Rk，＋∞）→R＋，使得下面结论成立：

对方程（3）的任一解z（t），设J为任意一个满足‖z（t）‖≥r0，∀t∈J的区间，r为任意一个满足r≥Rk的实数，如果t1，t2∈J，满足‖z（t1）‖≤r，‖z（t2）‖≥ζk（r），则z（t）在t1时刻与t2时刻之间绕原点顺时针旋转了至少k圈.

为了叙述方便，引入一些记号：

Sr为以原点为圆心半径为r的圆周；T j（t0，z0）为z（t；t0，z0）绕原点顺时针旋转j圈的时间；

由上面引理可知，当r充分大后T j（t0，z0）有意义，从而T＋（j；r）和T＿（j；r）都有意义.

引理5 如果条件（g0）成立，则对任意正整数j有T＋（j；r）＜＋∞，r≫1.

证明 当r≥r0并且充分大时，由引理3、引理4，存在实数r1，r2，满足r0＜r1＜r＜r2，使得任意在t0时刻从Sr上出发的解z（t；t0，z0）在完成绕原点顺时针旋转j圈之前跑不出区域Ω：＝｛（x，y）｜r1≤，由于a（t）是正周期函数，有A＞0.因此条件（g0），存在N0＞0及相应的α＞0，使得

3 对称周期解的稠密分布

由于方程（3）在原点性态不是很理想，通过它的Hamilton函数构造一个新的方程来弥补这一缺陷.设k（s）是光滑截断函数，满足k（s）＝1，s≥r20；k（s）＝0，s≤r20／2，其中r0来自引理3.定义新的Hamilton函数

在原点附近方程（5）为x′＝y，y′＝－2x，容易看出原点为该方程的平衡点，由初值问题解的存在唯一性可知从原点外任一点出发的解都不会经过原点.在半径为r0的圆域之外方程（5）为

显然此时与方程（3）一样.由此可知方程（5）的解是全局存在的，同时上面的所有引理对该方程同样成立.在证明定理之前先陈述一个引理.在文献［4］中该引理是针对Duffing方程（2）而言，不难验证其对方程（1）同样成立.

引理7 对于方程（1），

1）如果p（t）是偶函数，则解x（t）是偶次调和解的充分必要条件是存在整数m＞0，使得x′（0）＝x′（mπ）＝0.

2）如果g（x），p（t）是奇函数，则解x（t）是奇次调和解的充分必要条件是存在整数m＞0，使得x（0）＝x（mπ）＝0.

设z（t；0，z0）＝（x（t；0，z0），y（t；0，z0））是方程（5）在0时刻从z0＝（x0，y0）出发的解，其对应的极坐标形式为θ（t；0，z0），r（t；0，z0），并记θ0＝θ（0；0，z0），r0＝r（0；0，z0），则对方程（5）的解轨线有如下结果.

引理8 对于任意整数j＞0，存在实数r1及相应的正整数m与实数r2，满足r2＞r1＞r0，使得如下结论成立：

那么过点z0的解z（t；0，z0）满足

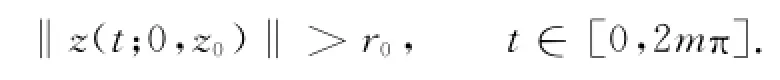
证明 由分析可知，对于方程（5），如果z0不为原点，则‖z（t；t0，z0）‖＞0，∀t∈R.又当x＝0，y≠0时，有

这说明解轨线只能顺时针穿过y轴.从而当‖z0‖≠0时有

对任意正整数j，在引理2.2中取k＝j＋2，则存在对应的Rk及单调递增函数ζk.任取r1满足

由引理5，存在m∈N，使得所有从Sr1上出发的解z（t；0，z0）旋转k圈的时间Δt≤2mπ，因此对任意（r0，θ0）∈Sr1，都存在t1（与θ0有关）满足0＜t1≤2mπ，使得θ（t1；0，z0）－θ0＝－2kπ.结合不等式（8），对任意z0∈Sr1有

定理1的证明 对于方程（5），在引理8中，取定整数j＝1，则存在相应的半径r1，r2（r2＞r1＞r0）及m∈N使得不等式（6），（7）成立.记z1＝（r0，0），z2＝（r2，0），则z1∈Sr1，z2∈Sr2，因此

令L为连接z1，z2的开直线段，此时不妨设θ0＝0，则

定义方程（5）的Poincare映射

L在p作用下所得曲线段P（L）是一段连续曲线，又方程（5）的零解具有唯一性，P（L）将不经过原点，从而由式（11）可知P（L）必将与x轴相交，即存在z0＝（a0，0）∈L，a0≠0，使得θ（2mπ；0，z0）＝－2π.因此方程（5）在0时刻从z0出发的解z（t；0，z0）＝（x（t，0，z0）），y（t；0，z0）满足

由引理8可知‖z（t；0，z0）‖＞r0，t∈［0，2mπ］.由于在半径为r0的圆域之外方程（3）与方程（5）是同一的，从而可知至少在［0，2mπ］的时间段内，z（t；0，z0）是方程（3）的解，并满足式（12）.利用方程（1）的对称性，由引理7可知x（t；0，z0）是其偶次调和解，记为x1（t）.对正整数j＝1，在不等式（9）中，用r1代替Rk，可同样证明存在满足引理8的r1′，r2′，m′，通过与上面的类似分析可得偶次调整和解x2（t），并且由不等式（10）有继续这一过程可得一列偶次调和解x k（t），满足

引理2的证明 首先在方程（3）中进行分析，设x1（t）的周期为n1，x2（t）的周期为n2，则n＝n1n2为他们的公共周期.令z1＝（a1，0），z2＝（a2，0）.定义方程（3）的Poincare映射

则z1，z2为P的不动点，即

设L0为连接z1，z2的开直线段，定义Lk（K≥1）如下：

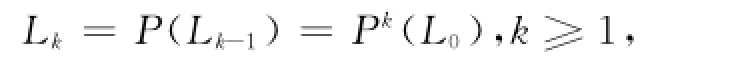
则Lk是以z1，z2为端点的简单开曲线段.对于Lk有如下2种可能：

情况1：存在k，使得Lk与x轴相交.此时存在z0＝（a0，0）∈L0，使得P k（z0）在x轴上.因此，存在方程（1）的解x（t），满足x（0）＝a0，x′（0）＝x′（2knπ）＝0.

情况2：对任意k＝1，2，3，…，Lk都与x轴不相交.由于P是保向和保面积同胚，利用类似文献［4］中的方法可证明

在同一坐标系下同时分析方程（3）与方程（5）.对方程（5），在引理8中取j＝1，则存在相应的r1，r2（r2＞及m∈N，使得不等式（6），（7）成立.由于因此存在整数k＞0，使得

取p i∈Lk∩Sri，并满足在p1，p2两点之间位于Lk上的曲线˜L与S r1，Sr2都不相交，通过简单分析可知˜L位于圆周Sr1，Sr2之间，显然p1，p2满足不等式（6），（7），此时不妨取θ0∈［0，2π］，则有

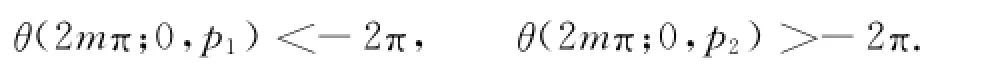
由引理8可知，方程（5）从p0出发的解z（t；0，p0）满足

而前面已经指明在半径为r0的圆域之外方程（3）与方程（5）是同一的，从而可知至少在［0，2mπ］时间段内，z（t；0，p0）也满足方程（3），且有θ（2mπ；0，p0）＝－2π.由于p0∈Lk，因此存在实数a0，满足a1＜a0＜a2，使得方程（3）满足初始条件x（0）＝a0，x′（0）＝0的解x（t；0，（a0，0）），y（t；0，（a0，0））满足：

则由解的唯一性可得

故无论是情况1还是情况2，上面的过程表明方程（1）都存在解x（t），满足a1＜x（0）＜a2，x′（0）＝x′（lπ）＝0其中l是正整数.由引理7知x（t）是方程（1）偶次调和解.对x1（t）和新产生的偶次调和解x（t）重复上面过程可得无数多个偶的次调和解.定理证毕.

［1］CAPIETTO A，DAMBROSIO W，PAPINI D.Superlinear indefinite equations on the real line and chaotic dynamics［J］.J Differential Equations，2002，181：419－428.

［2］PAPINI D.Infinitely many solutions for a Floquet－type BVP with superlinearity indefinite in sign［J］.J Math Anal Appl，2000，247：217－235.

［3］PAPINI D，ZANOLIN F.A topological approach to superlinear indefinite boundary－value problem［J］.Topol Methods Nonlinear Anal，2000，15：203－233.

［4］NAKAJIMA F.Even and periodic solution of the equation［J］.J Differential Equations，1990，83：277－299.

［5］钱定边.时间映射和跨共振点的Duffing方程［J］.中国科学：A辑，1993，23：471－479.

［6］丁同仁.常微分方程定性方法的应用［M］.北京：高等教育出版社，2004.

［7］DING Tongren，ZANOLIN F.Subharmonic solutions of second order nonlinear equations：A time－map approach［J］.Nonlinear Analysis TMA，1993，20：509－532.

［8］魏兰阁.一个Duffing方程的调和解和次调和解［J］.数学进展，2003，32：39－46.

Dense Distribution of Symmetric Periodic Solutions for a Class of Aymmetric Wquations with Weight

HE Tao1，DING Wei2
（1.Department of Basic Education，Nantong Shipping College，Nantong 226010，China；2.College of Science，Nantong University，Nantong 226007，China）

The problem of the symmetric periodic solutions’distribution for a class of symmetric subquardratic potential equations with positive weight is studied in this paper.Under some conditions，the fact that the distribution of symmetric periodic solutions is dense by phase plane analysis is proved.

subquardratic potential；Hamilton function；symmetric periodic solution；dense distribution

O 175

A

1000－1565（2011）03－0230－06

2010－10－27

何涛（1964－），男，江苏东台人，南通航运职业技术学院副教授，主要从事数学教育与应用研究.

丁卫（1983－），男，江苏南通人，南通大学讲师，主要从事常微分方程定性理论研究.

E－mail：dingwei＠ntu.edu.cn

王兰英）