基于薄膜线圈的高自旋弹丸转速测试方法研究*
2011-12-07曹咏弘范锦彪
曹咏弘,范锦彪,祖 静
(中北大学电子测试技术国家重点实验室,太原 030051)
0 引言
由于高自旋弹丸主要在弹道平面内飞行,且角速度主要是滚转角速度,可以利用一维传感器近似测量高自旋弹丸的转速,比如用一个沿弹轴方向的陀螺,用PSD或者PSD阵列,也可以遥测等[1],但成本都比较高。由于弹丸飞行时间较短,可以认为弹丸所飞过的区域内地磁场强度不变。这样就可以利用线圈式地磁传感器确定弹丸转速[2]。
关于线圈式地磁传感器的应用在国内已经有一些研究[3-10]。分析前人所做的工作,发现这些工作都是基于稳恒磁场中转子匀速转动的理论。弹丸的运动是一般刚体运动,在运动过程中,不仅有弹丸的自转角速度的变化,还有俯仰、偏航角的变化。稳恒磁场中转子匀速转动的理论不适合于一般的刚体运动。但是许多的实验结果却证明基于稳恒磁场中转子匀速转动的理论在实践中是可用的。文中利用电磁感应定律和刚体运动学的一般理论对平面磁感应线圈进行了研究,得到了线圈输出的一般公式,通过仿真发现只有在弹丸高自旋的情况下,在每一个滚转周期内,弹丸可以近似看作匀速的转动,因而可以近似应用稳恒磁场中转子匀速转动的理论,在不同滚转周期内,转动的角速度是不同的。
1 基于薄膜线圈的滚转角测试方法
薄膜线圈比手工缠绕的漆包线圈具有外观漂亮,工艺精湛,性能稳定,占用空间小,能够方便的粘贴于弹体的钢质结构表面,便于安装等特点。
薄膜线圈式地磁传感器测滚转角的基本原理是装在弹体内的柔性薄膜线圈在弹体飞行滚转时,传感器产生电动势,其输出信号带有弹丸运动的角速度信息,并随滚转角速度的变化而产生变化,因而可以反映弹体滚转的情况[3-11]。
考虑弹丸在飞行过程中运动是一般刚体运动的情形,由于平动不会造成磁通量的改变,所以研究刚体定点转动的情形。在定点转动情形下,刚体的转动轴在不断变化,角速度矢量也在不断变化,因而基于稳恒磁场中匀速转动转子的理论不再适用,需要重新推导。

图1 薄膜线圈传感器
1.1 一般刚体运动下线圈感应电动势的研究
假定空间有一个惯性坐标系Ox i y i z i,其沿坐标轴的单位矢量为i1、i2、i3(图2中未画出惯性坐标系),以及和载体固连的坐标系Oxyz,其沿坐标轴的3个单位矢量为 e1、e2、e3。S x、S y、S z 分别表示3个平面线圈的面积矢量,其面积大小分别为Sx、Sy、Sz,法线方向分别为 e1、e2 、e3,匝数分别为 nx、ny、nz,如图 2。
由高等动力学中的泊桑公式:

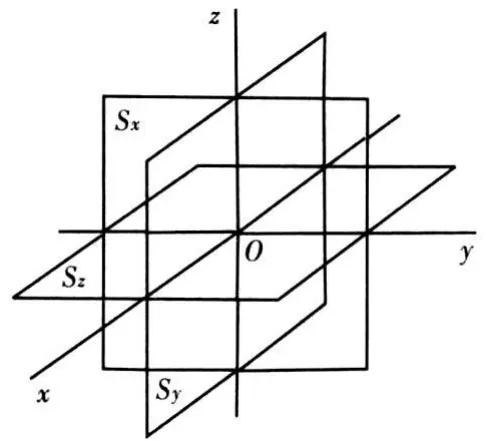
图2 三维线圈等效安装图
其中 ω是刚体转动角速度。
及法拉第电磁感应公式,可得:
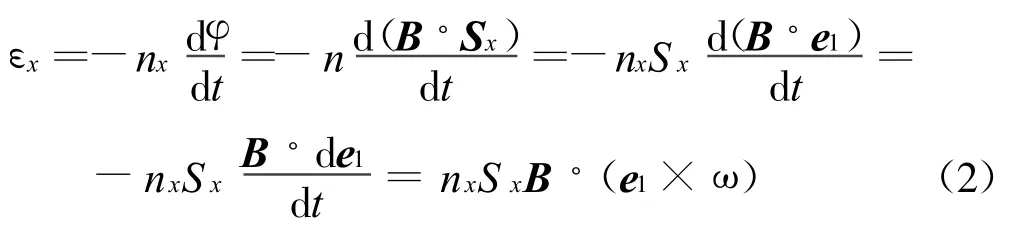
同理可得:
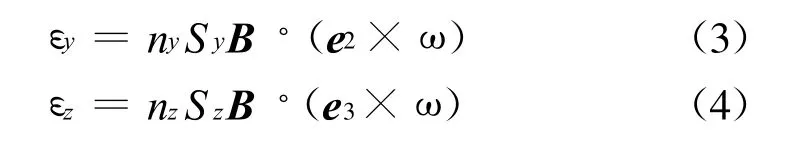
稳恒磁场中转子匀速转动时产生的感应电动势是上述一般公式的一个特例,现简单说明如下:假定z轴是弹丸的自转轴,来考察平面磁感应线圈Sx输出的感应电动势,在惯性坐标系Ox i y i z i下,B=B i1,而ω=ωi3,e1=cos(ωt)i1+sin(ωt)i2,即得熟知的εx=nxSxωsin(ωt)。这一特例验证了式(2)~ 式(4)的正确性。
可以利用式(2)来进行仿真,经过仿真发现,实际上式(2)可用于文献所述的转速测量情形只是高自旋或自旋是主要成分的情况,在这两种情况之外的应用,误差是较大的。下面通过实例来观察高自旋时线圈输出感应电动势的特征。
高自旋情况下,比如滚转角γ=40πt,偏航角变化很小,而俯仰角缓慢变化的情况下,通过仿真得到如图3的线圈输出曲线。当偏航和俯仰的幅值和周期取不同值时,仅影响局部地区的输出幅值,仍将得到类似于图3的输出曲线。
由图3可见,当弹丸高速自旋时,在一个滚转周期之内,线圈输出曲线可近似看成正弦或余弦曲线,一个近似正弦(余弦)波的一个周期即为弹丸旋转一周的时间,正弦波的零点和波峰、波谷是它的特征点,提取出这些特征点,通过计算它们之间的时间差,就可得到半周期τ,然后可以得出弹丸在每个半周期之内的近似转速n。

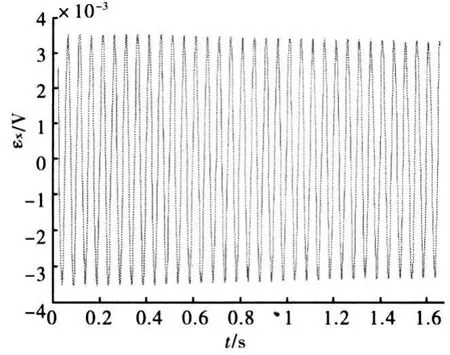
图3 弹丸高自旋时线圈输出曲线图
1.2 半周期的求法
半周期的求法有两种,一种基于求零点的半周期求法;另一种是基于求极值的半周期求法,即求波峰波谷的半周期求法。
1.2.1 基于求零点的方法
基于求零点的半周期求法依赖于零点的求法,由于弹丸转速很高,微小的零点误差,将会造成巨大的转速误差,因而准确地求出零点成为问题的关键,在以前的方法中零点的精度依赖于高采样频率,如果采样频率低,零点的精度就很低。但即使是高采样频率,出现真正的零点也是极其偶然的事,所以以往的做法都是认为最接近零点的点就是零点,但左接近值和右接近值对于高转速的情况仍然可以引起较大的误差。文中采用线性插值法来估计零点,可以大大提高零点准确度,进而提高半周期的计算准确度,从而可以在低采样频率下提高测试精度。
当一个单值连续函数的两个函数值满足条件f(i-1)≥0,f(i)≤0,或 f(i-1)≤0,f(i)≥0时,零点必在 f(i-1)和 f(i)之间,利用线性插值,可得发生零点的时间为
当数据在零点附近有噪声时,基于求零点的半周期求法可能出现误判,这时需要根据趋势人工干预。
1.2.2 基于求极值的方法
以极大值为例,如果x0是 f(x)的极大值点,由极大值的定义可知,在极大值点x0的左边,差分diff(f(x))都是正的,或者说如果对差分求符号函数的话,都等于1,即sign(diff(f(x)))=1,而在极大值点 x0的右边,diff(f(x))<0,sign(diff(f(x)))=-1。那么极大值点就是在当diff(sign(diff(f(x))))=2时。同理如果是极小值点,就有diff(sign(diff(f(x))))=-2。
实际上求极值点的方法更具有普遍性,在利用某些信号求转速时,由于可能不存在零点,但极值是存在的。求极值的方法也有一个风险,那就是由于噪声的存在,存在误判的可能,这时候需要根据实际情况人工干预。
通过记录相邻两个零点的时间差或两个相邻的极大值点和极小值点的时间差,可以得到半周期,利用半周期内弹丸滚转180°,计算出平均转速[7],连续求出各个相邻特征点时间段内的平均转速,然后对求出的各个平均转速进行曲线拟和,就可以得到近似反映弹丸在整个飞行时间内的转速曲线图。
2 实测数据分析
某型子弹全弹道转速测试系统的采样频率是25k Hz,采样时间为10s。图4是本次实弹实验测出的一组线圈感应电动势的波形图。
图4中的0.7s附近的毛刺是由于子弹发射时磁场强度突变所造成的干扰,最后的大毛刺是子弹最终落地撞击时的磁场强度变化的反映。从图中可以看出,0.7~1s的时间内,在很短的时间内,曲线由疏到密,表明转速在急剧增加,1~2s的时间内,曲线比较密集,表示转速很高,2s后曲线逐渐变稀,表明转速在逐渐减小,同时整个过程中感应电动势幅值的变化也印证了上面的分析。
将数据经小波降噪后[11-12],基于求零点的方法,求得每一个半周期τ,可得每个半周期之内的转速n,这是一些离散点,为了使数据看起来更平滑,采用样条函数进行了数据拟合。
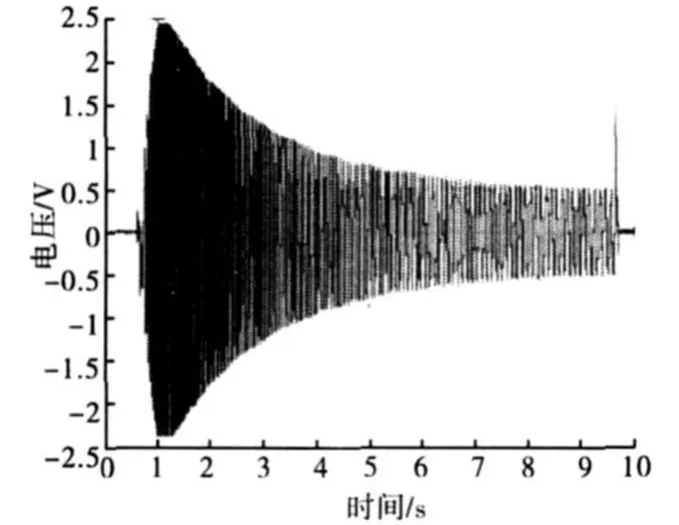
图4 薄膜线圈实测数据
图5 是得到的转速曲线。从中可以清楚地看到该子弹的转速变化规律:发射时转速急速增加,在1.1s时达到 3200r/s,而后转速逐渐变小,在 510r/s 时撞靶。测试数据与实弹测试时的遥测情况一致。
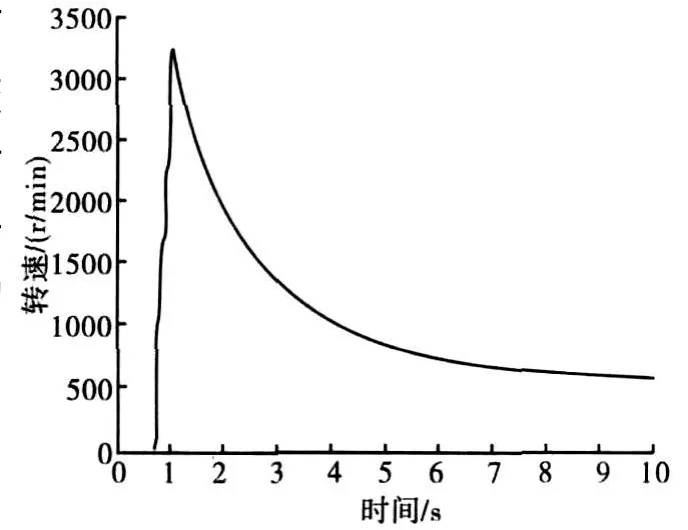
图5 子弹转速图
3 结语
文中研究了基于薄膜线圈的弹丸转速测试方法,首次推导了薄膜线圈在任意空间转动条件下输出感生电动势的公式,通过仿真总结出了线圈高自旋情况下的转速测试方法,研究了半周期的确定方法,并就某一工程问题进行了详细的分析,利用文中得到的转速数据和遥测结果一致,说明文中的方法是一种测高转速弹丸转速行之有效的方法。
文中所述求转速的方法也适合于利用具有类似特征的输出信号求转速的分析,比如磁强计等。
[1] 黄涛.弹丸转速的传感器测量方法[J].弹箭与制导学报,2002,22(4):69-74.
[2] 马铁华.存储测试技术的发展与应用及特种传感技术研究[R].北京:北京理工大学.1999.
[3] 李振华,贺安之,成灵安,等.基于地磁方位传感器的TSP关键参数测试技术[J].弹道学报,1998,10(2):58-63.
[4] 王广龙,祖静,张文栋,等.地磁场传感器及其在飞行体姿态测量中的应用[J].北京理工大学学报,1999,19(3):361-364.
[5] 沈波,陈荷娟,王志兴,等.基于地磁传感器的计转数引信可行性研究[J].探测与控制学报,2001,23(4):45-48.
[6] 沈波,黄晓毛,王志兴,等.基于地磁原理的计转数传感器技术研究[J].兵工学报,2003,24(3):313-315.
[7] 陈智刚,王志军,C N斯特列夫.运用地磁传感器对旋转弹进行程序控制[J].华北工学院测试技术学报,2001,15(3):169-174.
[8] 张卫华,侯文,杨瑞峰,等.地磁感应线圈法探测火箭弹的滚转运动[J].测试技术学报,2004,18(2):171-173.
[9] 韩兰懿,马铁华,范锦彪.地磁线圈对陀螺的修正技术[J].仪器仪表学报,2006,27(6):1294-1295.
[10] 李世中,耿生群,张亚.地磁式转数传感器盲区问题实验研究[J].弹道学报,2003,15(1):73-77.
[11] 胡昌华,张军波.基于MATLAB的系统分析与设计—小波分析[M].西安:西安电子科技大学出版社,1999.
[12] 崔夏荣.基于小波变换的信号降噪[J].南平师专学报,2005,24(4):89-91.
