一种简化的SAGE-HUSA卡尔曼滤波*
2011-12-07朱新岩
田 海,朱新岩
(解放军汽车管理学院,安徽蚌埠 233011)
0 引言
在无人机导航的实际应用中,由于对机载设备重量和体积上的严格限制,导航计算机在性能上有所限制,为了减少计算量,实际应用中一般采用降维模型。采用标准的卡尔曼滤波方法无法得到令人满意的导航精度,甚至导致滤波的发散。实际应用中多采用自适应卡尔曼滤波方法,目前常用的方法有强跟踪卡尔曼滤波、基于极大似然准则的自适应卡尔曼滤波、SAGE-HUSA自适应卡尔曼滤波等[1]。这些算法各有优缺点,在实际应用中存在着局限性。
为了解决常用自适应滤波算法在无人机实际应用中的局限性,在分析基于极大似然准则的自适应卡尔曼滤波和SAGE-HUSA卡尔曼滤波优点和缺点的基础上,结合两种滤波算法,给出了一种利用估计窗简化SAGE-HUSA卡尔曼滤波的简化的SAGEHUSA卡尔曼滤波算法。
1 基于极大似然准则的自适应卡尔曼滤波和SAGE-HUSA自适应卡尔曼滤波
基于极大似然准则的自适应卡尔曼滤波算法通过获取滤波过程中的残差(新息),利用残差对系统噪声方差阵Q和量测噪声方差阵R进行实时的估计和调整。
它是从系统量测值出现概率最大的角度出发对所关心的状态量进行估计,极大似然估计方法不但考虑滤波残差的变化,而且考虑残差协方差阵的变化规律。
它是通过保证在当前时刻的系统量测值相对于Q阵和R阵的调整参数的条件概率密度函数最大来对系统噪声方差阵Q和量测噪声方差阵R进行实时的估计和调整的算法。
而SAGE-H USA自适应卡尔曼滤波的主要目的是在噪声均值 qk、rk和协方差阵Q k、R k都未知的情况下,基于观测值Zk,Zk-1,Zk-2,…,Z1来求取噪声统计估值器和自适应卡尔曼滤波器。
对噪声均值及协方差的估计过程中,为了把过去时间久远的陈旧数据的作用逐渐弱化,而对离现在时间近的数据作用应加强。SAGE-HUSA自适应卡尔曼滤波采用渐消记忆指数加权法来加大较新数据项的加权系数,减小较陈旧数据项的加权系数。
再将通过统计估计得出的系统噪声和量测噪声的统计特性代入标准的卡尔曼滤波器中,即为SAGE-HUSA自适应滤波方法。
2 简化的SAGE-HUSA自适应卡尔曼滤波
SAGE-HUSA自适应卡尔曼滤波方法[4]相对于基于极大似然准则的自适应卡尔曼滤波而言,其改进在于引进了遗传因子b,进而增加了距离当前时刻较近的观测值的权重,相应减小了较陈旧数据对参数估计的影响。
但SAGE-HUSA自适应卡尔曼滤波方法在对系统噪声方差阵Q和量测噪声方差阵R的估计过程中,需要用到从滤波开始时刻到当前时刻所有的量测值随着时间的推移,Q阵和R阵的计算量逐渐增大,对导航计算机的负担增加;另外遗忘因子b的取值需要验前信息,有一定的风险性。为了减少计算量,并弱化遗忘因子所起的作用,可以结合基于最大似然估计的自适应滤波方法,采用估计窗对Q阵和R阵进行估计[2-3]。但是估计窗的在线确定有一定的风险,体现在估计窗过大,滤波结果的无偏性较好,但可能导致无人机的动态性能表现较差;估计窗过小,虽然能够较好的反映系统模型的变化,但是不能充分应用观测值所包含的信息,不能保证滤波过程的无偏性,严重的情况甚至导致滤波的发散。
针对估计窗难以确定这一问题,给出了通过计算残差变化率来确定估计窗范围的自适应滤波方法。考虑到SAGE-HUSA自适应卡尔曼滤波对Q阵和R阵的实时估计是通过新息来实现的,而当系统模型发生变化或者无人机的动态性能改变时,新息也有较大的变化。滤波非最优时,新息随时间变化如图1所示。
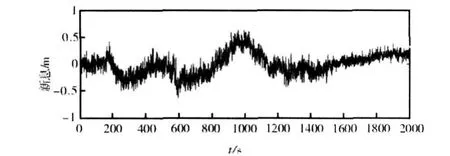
图1 新息随时间变化图
由于噪声的影响,新息的变化关系不容易看出,在滤波最优状态下,新息符合白噪声序列,由于系统的模型和噪声方差不知或者不能准确知道,通常导航系统采用的是次优滤波,新息不是白噪声。由于新息序列满足马尔科夫性质,因此,对新息序列的描述可用下面解析式近似描述[5]:
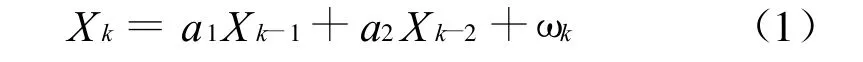
式中:a1、a2在一定的区域范围内为未知固定参数;ωk为白噪声。为了去除ωk对分析新息曲线走势带来的影响,采用对新息求平均的方法,即取:

得到如图2所示的去除噪声后的曲线走势。
由于ωk为白噪声,即当取超过一定量数值后,有:

即可去除噪声影响,式(2)可以简化为:

将式(4)代入式(5),可以近似得到:
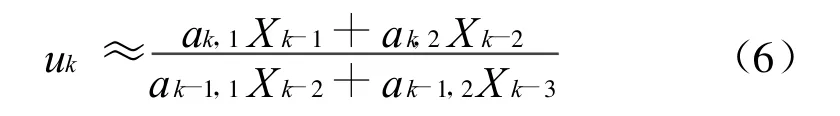

图2 去除噪声后新息的走势
由于去除噪声后,相邻信号数值接近,因此,uk取值主要由常系数决定,在解析关系相同的区域内,有uk≈1,而在解析关系发生变化时,该式不成立。u值变化曲线见图3。
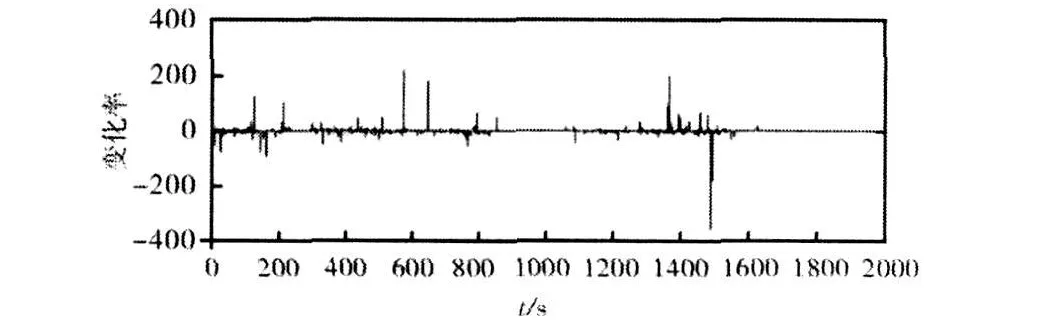
图3 u值随时间变化曲线
通过这种方法可以确定估计窗的取值范围。在解析关系变化的时刻,需要滤波能够较好的反映系统模型的变化,对无人机的动态性能更敏感,可以取较小的估计窗范围;而在变化相对较为和缓的区域,则考虑取较大的估计窗范围,使滤波能够保持较好的无偏性。该算法的流程如图4所示。

图4 改进的自适应滤波算法流程图
3 仿真
为了验证简化的SAGE-HUSA自适应滤波方法的实际效果,并对比该方法和其他自适应滤波方法的优劣,文中对标准卡尔曼滤波、基于极大似然准则的自适应滤波方法、SAGE-HUSA自适应滤波方法、改进后的SAGE-HUSA自适应滤波方法进行了仿真分析。
仿真条件如表1所述,以东向位置误差为例。为了说明问题,在程序编写过程中,有意的改变方差阵以偏离仿真中实际给出的方差。

表1 无人机飞行仿真状态及参数设计
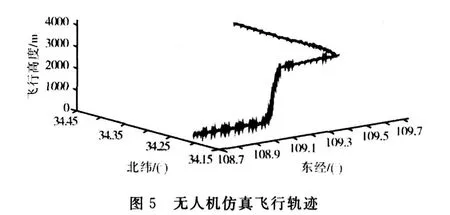
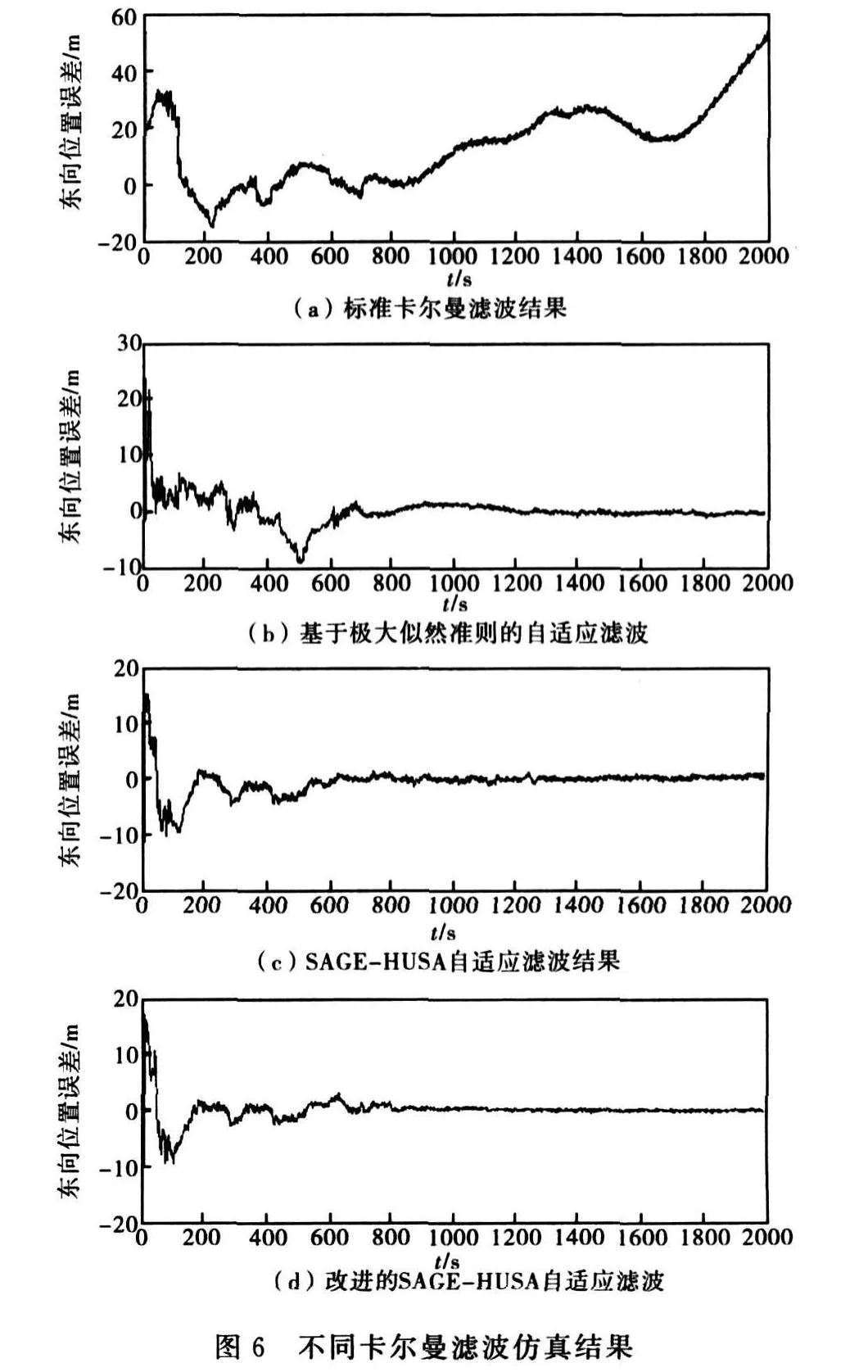
仿真结果表明,当系统方差阵Q k、R k偏离实际数据时,采用标准的卡尔曼滤波方法,估计精度差且很快趋于发散;基于极大似然准则的自适应滤波方法收敛快,精度高,但是估计窗的合理选取较为困难,估计窗的选取对滤波效果影响较大,其对滤波的无偏性、收敛性都有较大的影响,对于无人机导航系统而言,该方法存在着局限性;而SAGE-HUSA自适应滤波方法通过测量值在线估计均值及方差,能够有效的遏制滤波的发散,且相比较基于极大似然准则的自适应滤波方法,保持了滤波的无偏性,但是标准的SAGEHUSA自适应滤波方法在无人机长时间的飞行过程中计算量偏大,不适合无人机导航过程中对计算量的要求;而简化后的SAGE-H USA自适应滤波方法方法简单、计算量小,可以有效遏制滤波的发散,能够满足无人机导航工程应用的需要。
4 结论
1)采用简化后SAGE-HUSA自适应滤方法对导航参数进行估计其精度优于标准的卡尔曼滤波;
2)从实际应用的角度来看,该方法结合了基于极大似然准则的卡尔曼滤波方法和SAGE-HUSA自适应滤波方法的优点,相比较其它方法,减少了计算量,降低了估计窗的选取难度;
3)该方法结合了基于极大似然准则的卡尔曼滤波方法和SAGE-HUSA自适应滤波方法的优点,在保留了估计精度的基础上,减少了对无人机飞行状态中机动性的反应时间;
4)该方法在线参数估计的实用性优于基于极大似然准则的卡尔曼滤波方法和SAGE-H USA自适应滤波方法,能够满足无人机自主导航对参数精度、实时性、计算量的要求。
[1] Gerlach K,Outlier resistant adaptive matched filtering[J].IEEE Transactions on Aerospace and Electronic Systems,2002,38(3):885-901.
[2] Qi Song,Zhe Jiang.Noisecovarianceidentification based adaptive UKF with application to mobile robot systems[C]//IEEE International Conference on Robotics and Automation Roma,2007:4164-4169.
[3] 周露,李东江,闻新.具有随机偏差的最优多段卡尔曼估值器[J].系统工程与电子技术,2003,25(7):790-792.
[4] 沈云锋,朱海,莫军,等.简化的Sage-Husa自适应滤波算法在组合导航中的应用及仿真[J].青岛大学学报,2001,16(1):44-48.
[5] 王社伟,张洪钺,陶军.基于半马尔可夫过程的容错导航系统可靠性分析[J].航天控制,2006,24(2):84-87.
