时滞中立型线性系统的时滞相关非脆弱控制器设计
2011-12-02刘美静马跃超
刘美静,马跃超
(燕山大学 理学院 河北 秦皇岛 066004)
时滞中立型线性系统的时滞相关非脆弱控制器设计
刘美静,马跃超
(燕山大学 理学院 河北 秦皇岛 066004)
研究了时滞中立型线性系统的时滞相关非脆弱控制器设计问题,分别对非脆弱控制器的乘性与加性加以讨论.通过构造适当的Lyapunov泛函,利用Schur补引理和最近提出的积分不等式,得到了时滞相关非脆弱控制器的设计方法.利用matlab中的线性矩阵不等式工具箱进行求解,数值仿真说明了该设计方法的有效性.
中立型系统; Lyapunov泛函; 线性矩阵不等式; 非脆弱控制
0 引言
中立型系统不仅广泛存在于工程实际中,而且许多实际系统可以转化为中立型系统来研究,因此,中立型时滞系统的鲁棒控制问题受到了学者的广泛关注[1-3].文献[2]研究了一类不确定中立型时滞系统的状态反馈鲁棒控制问题;文献[3]研究了具有时变不确定性的中立型系统的鲁棒镇定问题.由于仪器精度不足和舍入误差等因素,在控制器本身实现过程中,控制器参数会发生变化,这将破坏闭环系统的稳定性,使其性能下降,即控制器本身是脆弱的.因此,关于非脆弱控制器的设计问题引起了国内外学者的极大兴趣[4-7].文献[4]首次提出了非脆弱控制器的思想;文献[7]研究了中立型系统的基于观测器的非脆弱H∞控制问题.
本文在文献[5-7]基础之上,针对一类不确定中立型时滞系统,讨论了时滞中立型线性系统的时滞相关非脆弱控制器设计问题.利用Schur补引理和最近提出的积分不等式,给出了不确定中立型时滞系统的鲁棒H∞控制器的设计方法.利用matlab 的线性矩阵不等式(LMI)工具箱求解非常方便.本文所考虑的系统状态含有时滞,中立导数项含有不确定性,从而使本文所取得的结果适用范围更广一些.
1 问题描述
考虑不确定系统
(1)
式中,x(t)∈Rn,w(t)∈Rq,u(t)∈Rm,z(t)∈Rp分别为系统的状态,扰动输入,控制输入及受控输出,且w(t)∈L2[0,∞),φ(t)为[-h,0]上的连续可微初始函数,h=Const.>0为系统状态时滞.系数矩阵A0,A1,B1,B2,L0,D1,D2,C为具有适当维数的常数实矩阵,ΔA0,ΔA1,ΔB1,ΔL0,ΔL1,ΔD1,ΔC为时变参数不确定性,假设具有形式
(2)
式中,H1,H2,E0,E1,E2,E3有适当维数的常数实矩阵,F(t)为时变未知实矩阵,满足F(t)TF(t)≤I.
考虑非脆弱控制器
u(t)=(K+ΔK)x(t),
(3)
式中,K为控制器增益,ΔK为扰动矩阵,属于下列两种情形之一:
情形1(乘性不确定性) ΔK依赖于控制器增益K,满足
ΔK=HaFa(t)EaK;
(4)
情形2(加性不确定性) ΔK不依赖于控制器增益K,满足ΔK=HbFb(t)Eb.

系统(1)在非脆弱控制器(3)的作用下导出闭环系统(5),t∈[-h,0],

(5)
本文设计如(3)的非脆弱控制器,使得(5)内部稳定,且在零初始条件下具有给定的H∞扰动抑制水平γ,即满足‖z(t)‖2<γ‖w(t)‖2,∀0≠w(t)∈L2[0,∞).

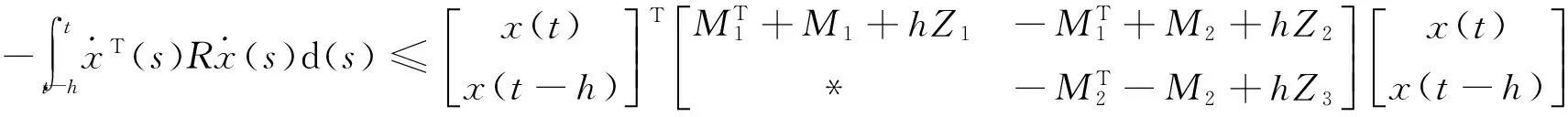
(6)
引理2[9]给定矩阵Σ=ΣT,以及适当维数的矩阵H,E,则Σ+HFE+ETFTHT<0.对任意满足FTF≤I的F成立的充要条件是存在ε>0,使得Σ+ε-1HHT+εETE<0.
2 主要结果
2.1时滞相关有界实条件
引理3给定γ>0并假设‖C‖+‖H1‖‖E3‖<1.如果存在n×n实矩阵P>0,R>0,Q1>0,Q2>0及M1,M2,Z1,Z2,Z3使得矩阵不等式(7)成立,
(7)
其中,
(8)
则系统(1)在非脆弱控制器(3)的作用下不仅渐近稳定,且在零初始条件下具有给定的H∞扰动抑制水平γ.
证明取Lyapunov-Krasovskii泛函

对V(t,xt)沿闭环系统(5)的轨线求导数,得到
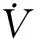
(9)
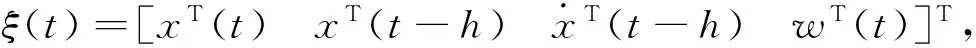
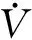

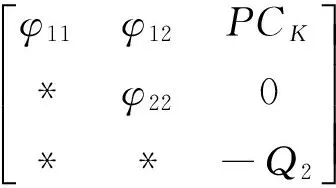
由Lyapunov-Krasovskii稳定性定理知(5)内部渐近稳定.

2.2情形1的非脆弱H∞控制器设计
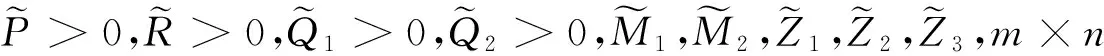
(10)

(11)
其中,
(12)
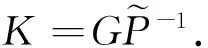
证明将不确定性矩阵(2)及(4)带入矩阵不等式(7),则(7)成为
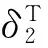
(13)
其中,
两次应用引理2有,
(14)
由Schur补引理,不等式(14)等价于

(15)
下面分两步证明结论.首先,不等式(10)等价于式(15),由于(14)与(15)等价,(14)成立就有(13)成立,即(7)成立;其次,若不等式(11)成立,就有不等式(8)亦真.

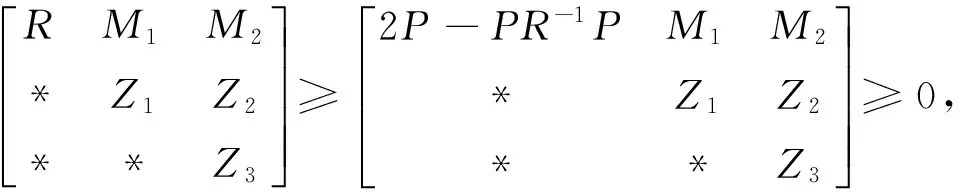
2.3情形2的非脆弱H∞控制器设计
对于情形2,类似于定理1 的证明,可得定理2.
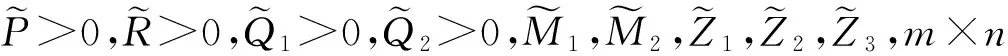
(16)
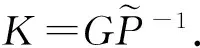
说明定理1和定理2分别针对情形1和情形2给出了非脆弱H∞控制器的设计方法,只要给定定理的LMIs有解,就可以找到形如(3)的非脆弱控制器,这就是设计非脆弱控制器的过程.此外,G和P-1也都可以通过给定的LMIs来求解.
3 数值仿真

当h=0.8时,情形1和情形2两种情况所获得的非脆弱控制器增益矩阵K分别为:
4 结束语
本文研究了一类不确定中立型系统的时滞相关非脆弱控制问题.针对非脆弱控制器的乘性与加性两种不确定形式,利用Lyapunov-Krasovskii泛函方法、Schur补引理和最近提出的积分不等式,给出了非脆弱控制器的设计方法.
[1] Niu Y, Lam J, Wang X. Sliding-mode control for uncertain neutral delay systems[J].IEE Proc-control Theory Appl, 2004, 151(1):38-44.
[2] 徐兆棣, 李晓毅. 不确定中立型时滞系统的鲁棒控制-LMI方法[J]. 电机与控制学报,2005, 9(2): 116-118.
[3] 李明, 胡广大. 不确定中立型系统的改进的时滞依赖的鲁棒镇定[J]. 系统仿真学报,2007, 19(17): 4037-4041.
[4] Keel L H , Bhattacharyya S P. Robust, fragile, or optimal[J]. IEEE Trans on Automatic Control, 1997,42(8):1098-1105.
[5] 王武, 杨富文. 不确定时滞系统的时滞依赖鲁棒非脆弱H∞控制[J]. 控制理论与应用,2003, 20(3): 473-476.
[6] Xu S Y, Lam J, Wang J. Non-fragile positive real control for uncertain linear neutral delay systems[J]. Systems & Control Letters, 2004, 52(1): 59-74.
[7] Lien C H. Non-fragile guaranteed cost control for uncertain neutral dynamic systems with time-varying delays in state and control input[J]. Chaos, Solitons and Fractals , 2007, 31 (4): 889-899.
[8] Zhang X M, Wu M, She J H. Delay-dependent stabilization of linear systems with state and input delays[J]. Automatica, 2005, 41(8): 1405-1412.
[9] Xie L H . Output feedbackH-infinite control of systems with parameter uncertainly[J]. Int J Control, 1996, 63(4): 741-750.
Delay-dependentNon-fragileControllerDesignforTimeDelayNeutralLinearSystems
LIU Mei-jing, MA Yue-chao
(CollegeofScience,YanshanUniversity,Qinhuangdao066004,China)
The problem of the delay-dependent non-fragile controller design for time delay neutral linear systems was studied.Both cases of non-fragile controller for multiplicative and additive were considered. By constructing appropriate Lyapunov functional, using Schur theory and the recently proposed integral inequality, the design method of non-fragile controller was obtained. By using the LMI of matlab, an illustrative example showed the effectiveness of the proposed method.
neutral systems; Lyapunov functional; linear matrix inequality(LMI); uncertainly; non-fragile control
TP 273
A
1671-6841(2011)03-0053-06
2010-04-07
国家自然科学基金资助项目,编号60974004.
刘美静(1984-),女,硕士研究生,主要从事广义中立型系统研究,E-mail:liumeijing0315@126.com.
