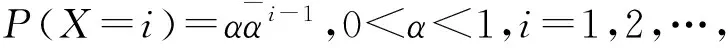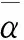带单重工作休假和休假中断的GeoX/Geo/1排队
2011-12-02贾礼君刘春平徐秀丽
贾礼君,刘春平,徐秀丽,刘 雷
(燕山大学 理学院 河北 秦皇岛 066004)
带单重工作休假和休假中断的GeoX/Geo/1排队
贾礼君,刘春平,徐秀丽,刘 雷
(燕山大学 理学院 河北 秦皇岛 066004)
分析了带休假中断的成批到达的单重工作休假GeoX/Geo/1排队系统.针对具体的系统模型,利用拟生灭过程和迭代方程,得到系统的稳态队长分布,从而得到系统的平均稳态队长以及随机分解结果.利用负二项式分布的性质,讨论了顾客等待时间的上下界,进而求得平均等待时间的上下界.最后进行了数值分析,考察了系统参数变化对平均队长和平均等待时间的影响.
GeoX/Geo/1排队系统; 单重工作休假; 成批到达; 休假中断
0 引言
休假期间服务员将以较慢的速率接待顾客,而不是完全停止对顾客的服务,称为工作休假(working vacation, WV).工作休假策略可以节约系统的运行成本[1-5].本文将休假中断引入到成批到达的离散时间工作休假排队中,在休假中断策略下,当系统在工作休假状态完成一个顾客的服务时,若系统中还有顾客等待,原本处于工作休假状态的服务台可以转入正常的工作状态,这样就减少了顾客的等待时间.因此,本文对带休假中断的成批到达的离散时间工作休假排队进行分析,将更有现实意义和应用价值,丰富了离散时间工作休假排队系统的模型.
1 模型描述

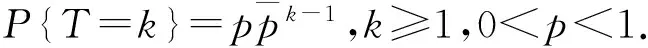
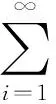
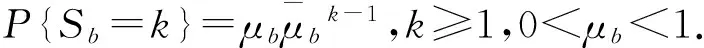

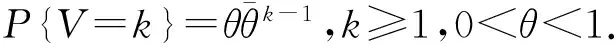
假设休假开始和结束都发生在时隙末端(n-n)上.工作休假结束时,若系统中有顾客等待,则开始进入忙期,若系统中无顾客等待,则系统进入闲期,直到系统中有顾客到达时系统进入忙期;在工作休假期间,若有顾客到达,服务台对顾客进行低速率服务,当服务完成时(休假未结束),若系统中有顾客,则立即结束休假(即发生了休假中断),开始高速率服务其他顾客,直到系统中无顾客;若系统中无顾客,则进入闲期,若在休假期内有顾客到达且当休假结束时正在接受服务的顾客服务未完成,则立即转换为高速率重新进行服务.
4)假设到达间隔T、服务时间Sb和Sv、休假时间V都是相互独立的,先到先服务(FIFO)排队规则为:
设Qn表示时隙分点n+时刻系统中的顾客数,记Jn=0(时刻n+系统处于工作休假状态),Jn=1(时刻n+系统处于非工作休假状态),{(Qn,Jn),n≥0} 是一个MC,有状态空间Ω={(k,j):k≥0,j=0,1}.
将MC的状态按字典序排列,其转移概率矩阵可表示成分块三对角形式,

2 稳态队长及其随机分解
假设以(Q,J)表示过程(Qn,Jn)的稳态极限,记

由平衡方程可以得到:
(1)
(2)
(3)
(4)
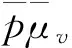
(5)
(6)
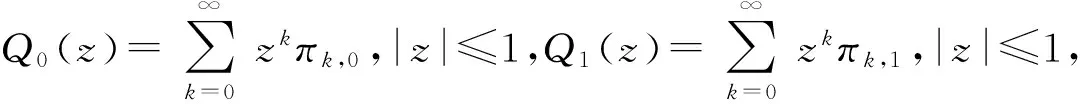
定理1如果ρ=pE(X)/μb<1且μb>μv,则稳态队长Q可以分解为两个相互独立的随机变量的和,Q=L0+Ld,其中L0是无休假GeoX/Geo/1排队稳态队长,它的PGF是

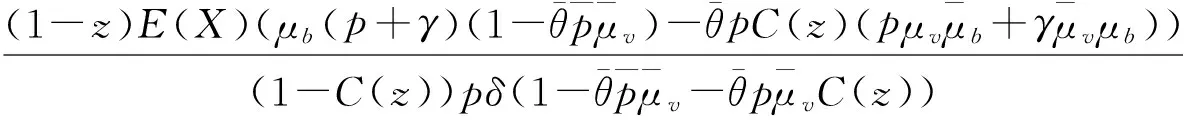
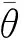
证明将(2)和(3)的每一个方程分别乘以一个适当的zn,相加整理可得

(7)
同样,将(4)和(5)的每一个方程分别乘以一个适当的zn,相加整理可得
Q1(z)=(p(p-θpC(z)+γ(1-C(z)))π0,0-pΨ(z)(Q0(z)-π0,0)+γΦ(z)π0,0)/(pΦ(z)),
(8)
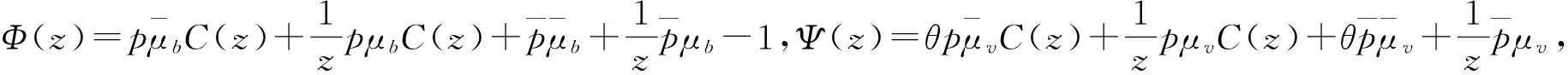
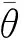
(9)
显然,当μb>μv时式(9)的分子大于0,这时分母也大于0,即μ0-pE(X)>0,因此ρ=(pE(X))/μb<1,另外,由(8)还可得到
π0,0=(μb(1-ρ))/δ,
(10)


证毕.
3 等待时间分析
将W和W(z)分别定义为稳态下顾客的等待时间及其PGF,由随机序理论可以得到等待时间在矩母函数序中的上下界,从而可以求得平均等待时间E(W)的上下界.
定义1设X和Y为两个非负随机变量,且E(zX)≥E(zY),z∈(0,1),则X以矩母函数序小于Y,记为X≤mgfY.
引理1设X和Y为两个非负随机变量,如果X≤mgfY,则E(X)≤E(Y)(假设期望均存在).证明见文献[6].
定理2如果ρ=pE(X)/μb<1且μb>μv,则稳态等待时间W在矩母函数序中存在上下界,即W2≤mgfW≤mgfW1,其中W1,W和W2的PGF分别是W1(z),W(z)和W2(z),且
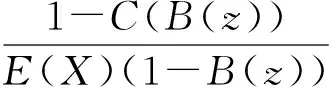
证明为了得到W(z),我们分析3种可能的情况:
(a)当一批顾客在状态 (k,1)(k≥1)到达时,批内一个顾客的等待时间是这批之外的k个顾客的服务时间与在这批内的等待时间之和,这里所有的顾客都是在忙期接受服务,利用文[7]的内容可以得到:
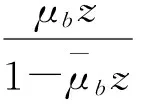
(11)
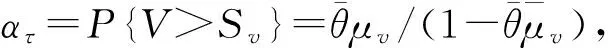


(12)
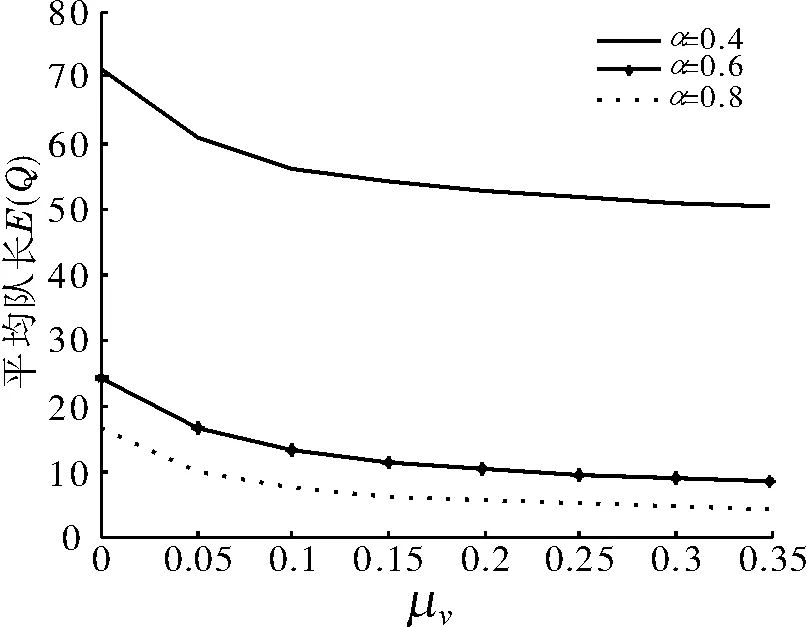
(c)当一批顾客在状态(0,0)到达时,若V>Sv,则当批内的第一个顾客以μv被服务完成时,批内剩余的顾客均以μb接受服务;若V (13) 由(11)、(12)、(13)可得: 显然,W1(1)=1,W2(1)=1,所以假设W1(z)和W2(z)分别是随机变量W1和W2的PGF,由定义1可得W2≤mgfW≤mgfW1,进而由引理1可以得到平均等待时间E(W)的上下界,即E(W2)≤E(W)≤E(W1). (14) 备注1如果顾客在工作休假期停止工作,即μv=0,模型将退化为GeoX/Geo/1经典休假排队;进一步如果θ→∞,模型将退化为GeoX/Geo/1无休假排队,见文献[7]. 备注2如果一批到达的顾客数始终为1,即c1=P{X=1}=1,且没有休假中断,则模型将退化为单重工作休假Geo/Geo/1排队,见文献[8]. 假设系统中的参数p=0.3,μb=0.8,θ=0.1,图1是参数变化对E(Q)的影响,图2是参数变化对E(W)的影响.可以看到:1)当其他参数不变时,系统的平均队长随着服务率μv的增加而减小,随着α的增加而减小;2)随着服务率μv的增加,E(W)的上界E(W1)和下界E(W2)的曲线越来越接近,这说明我们的研究结果符合实际情况. 图1 μv对E(Q)的影响Fig.1 Effection of μv on E(Q) 图2 μv对E(W)的影响Fig.2 Effection of μv on E(W) [1] Servi L D,Finn S G.M/M/1queue with working vacations (M/M/1/WV)[J].Performance Evaluation,2002,50(1):41-52. [2] Wu D A,Takagi H.M/G/1 queue with multiple working vacations[J].Performance Evaluation,2006,63(7):654-681. [3] Bata Y.Analysis of aGI/M/1 queue with multiple working vacations[J].Operations Research Letters,2005,33(2):201-209. [4] Banik A,Gupta U,Pathak S.On theGI/M/1/Nqueue with multiple working vacations-analytic analysis and computation[J].Applied Mathematics and Computation,2007,31(9):1701-1710. [5] 田乃硕.休假排队综述[J].运筹学杂志,1994(13):5-11. [6] Moshe S,George S J.Stochastic Orders and Their Applications [M].NewYork:Academic Press,2005:126-128. [7] 孙荣恒,李建平.排队论基础[M].北京:科学出版社,2002:226-227. [8] Li Jihong,Tian Nianshuo.Analysis of the discrete time Geo/Geo/1 queue with single working vacation[J].Quality Technology& Quantitative Management,2008,5(1):77-89. AnalysisofGeoX/Geo/1QueuewithSingleWorkingVacationsandVacationInterruptions JIA Li-jun,LIU Chun-ping,XU Xiu-li,LIU Lei (CollegeofScience,YanshanUniversity,Qinhuangdao066004,China) A bulk input GeoX/Geo/1 queue with single working vacations and vacation interruptions was analyzed.Firstly, using quasi birth and death chain and iteration method, distributions of stationary queue length were obtained, and the stochastic decomposition result for the PGF of the stationary queue size was given.Furthermore, the upper bound and the lower bound of the sojourn time of a customer was discussed with the property of negative binomial, and the PGF was given.Finally, some numerical analyses were carried out, and the parameters’ effect on the queue length and waiting time was investigated. GeoX/Geo/1 queue; single working vacation; bulk input; vacation interruption O 226 A 1671-6841(2011)03-0001-05 2010-05-06 国家自然科学基金资助项目,编号10671106;河北省自然科学基金资助项目,编号F2008000864;燕山大学博士基金资助项目,编号B228. 贾礼君(1982-),男,硕士研究生,主要从事休假排队理论分析及应用研究,E-mail:liuchunping1982@163.com.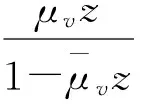

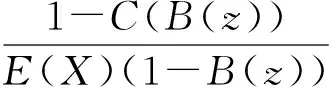

4 数值例子