第二型二元含参量正常积分函数的分析性质

顾先明

（唐山师范学院 数学与信息科学系，河北 唐山 063000）

第二型二元含参量正常积分函数的分析性质

顾先明

（唐山师范学院 数学与信息科学系，河北 唐山 063000）

根据含参量正常积分（积分限量函数的情形）的定义，类似地给出了第二型含参量正常积分函数的定义。研究发现第二型二元含参量正常积分函数在其定义域上具有连续性、可微性、可积性等分析性质，最后给出了一些应用实例。

含参变量正常积分函数；连续性；可微性；可积性

1 引理及预备知识

许多数学分析（或微积分学）教材都对含参变量正常积分做了较为细致的研究，均得到了含参量正常积分在其定义域上，当被积函数满足一定条件后可以具有连续性、可微可积性等结果，但后继的研究多集中在对已有结果的条件做改进或推广，对含参量正常积分中被积函数推广研究不多见。文[1]把含参量正常积分（积分限量为常数）的被积函数推广到三元函数（甚至是n元函数）后，定义了一类二元含参量正常积分函数，并发现它在定义域上也具有连续性、可微性、可积性。本文将含参量正常积分（积分限量为常数）的被积函数推广到三元函数，相应的积分限函数推广到二元函数。然后定义了一类第二型二元含参量正常积分函数，进而探讨该类函数的分析性质，并给出了一些实例。

定义1 一般地设f(x,y,z)为定义在区域

G ={(x, y, z) |α(x, y) ≤z ≤ β(x, y )(x, y) ∈ [a, b ]×[c, d ]}

上的三元函数，其中α (x ,y),β(x,y)为定义在矩形区域

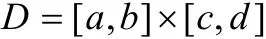
上的连续函数，若对于

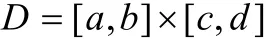
上有一固定点P( x, y)， f( x, y, z)作为z的函数在闭区间

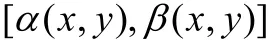
上可积，则其积分值是(x,y)在矩形区域

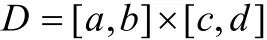
上取值函数，记作F(x,y)，则有

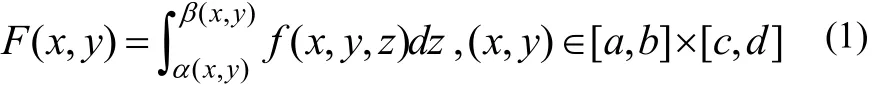
把形如⑴式的函数称为第二型二元含参量正常积分函数（以下简称函数(1)）。

引理1 若 f( x,y,z)是定义在有界闭区间D上的连续函数，那么函数 f( x,y,z)在D上必可积。

引理 2 设函数f(x,y)的各偏导数在点( x0, y0)的某个邻域上存在偏导数，在( x0, y0)点连续，那么f在点(x0,y0)处可微。

定理1 设函数f(x,y,z)为定义在区域

G ={(x, y, z) |α(x, y) ≤z ≤ β(x, y )(x, y) ∈ [a, b ]×[c, d ]}上的连续函数，其中α (x ,y),β(x,y)为矩形区域

2 主要结果及证明

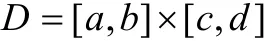
上的连续函数，则函数

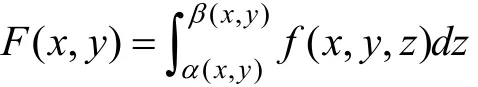
在区域

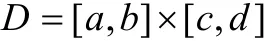
上连续。

证明 设P0( x0,y0)为 D= [a,b ]×[c,d ]

上任意一点，要证：

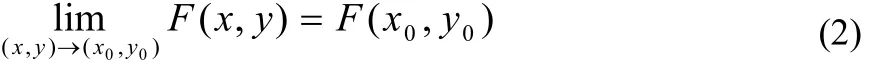
因为

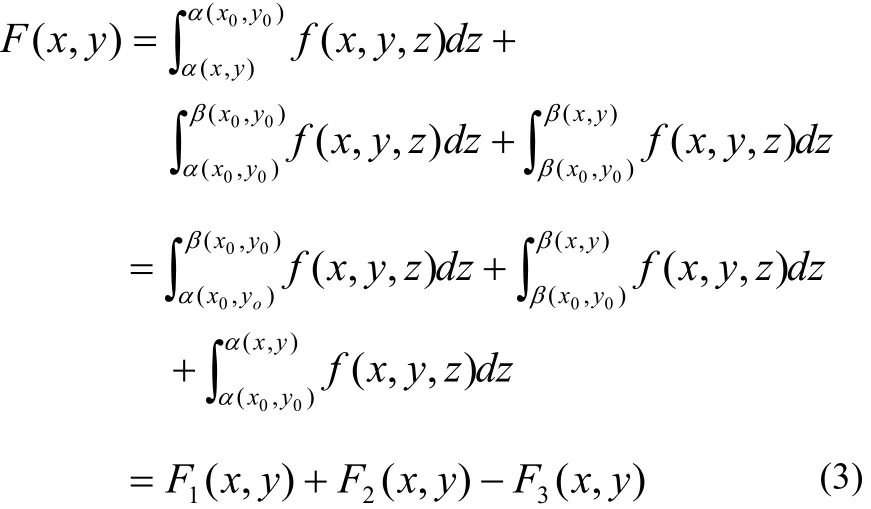
其中F1( x, y)，F2( x, y)，F3( x, y)分别为上式右端的三个积分。积分 F1(x,y)的积分限量是常数，满足文[1]的条件，故

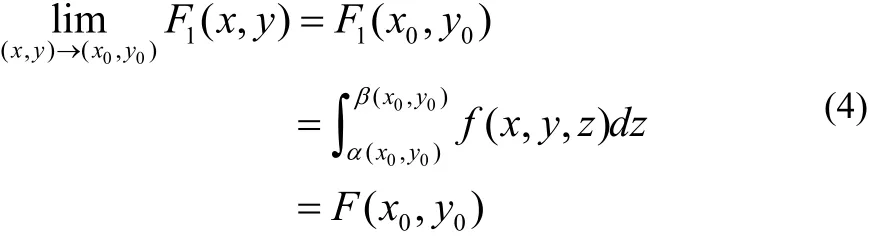
另外

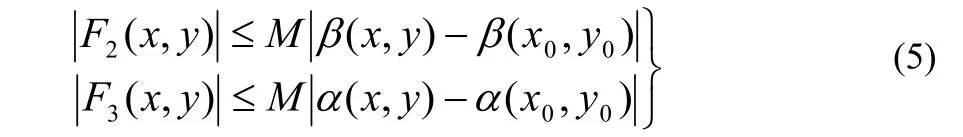
其中

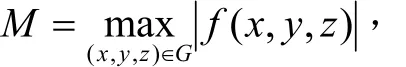
再根据 α(x ,y),β(x,y )的连续性，知(5)式右端趋于零，当(x, y)→ (x0,y0)时，从而

由(3)、(4)及(5)式即知(2)式正确。证毕。

定理2 设 f( x, y, z) , fx'( x, y, z) , fy'(x, y, z )都在长方体区域

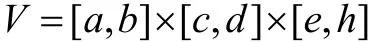
上连续，又设 α(x ,y),β(x,y)在矩形区域

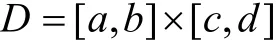
上具有连续偏导数，且满足

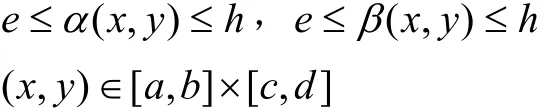
则函数

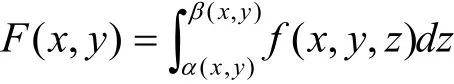
在D= [a,b ]× [c,d]上分别关于x,y可微，即

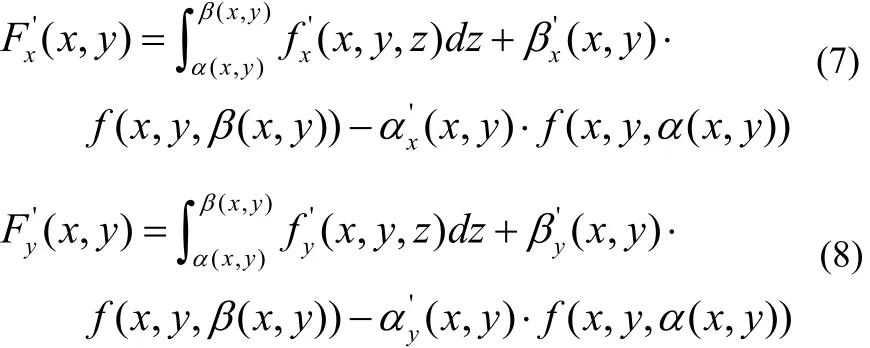
证明 这里只证(7)，(8)类似。

由于 F1(x,y)的积分限量是常数，满足文[1]中定理3的条件，故有

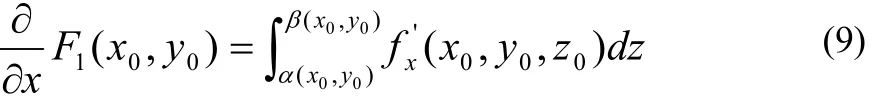
此外，由积分第一中值定理，可知

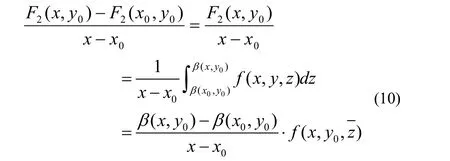
其中z在 β( x0, y0)与β( x,y0)之间，令(10)式中 x→ x0，并注意到此时→β(x0,y0)，即得

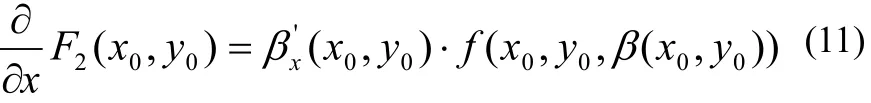
同理可证

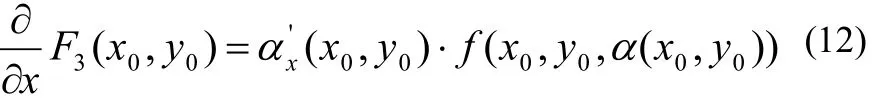
由(3)、(9)以及(11)、(12)，即知(7)当 (x,y)= ( x0, y0)时成立，由( x0, y0)可为矩形区域 D= [a,b] × [c,d ]中任一点，故知(7)对一切 (x, y)∈ [a,b]× [c,d]都成立。证毕。

推论1 若函数 f( x,y,z)满足定理2的条件，则函数F (x,y)在矩形区域 D= [a,b ]× [c,d ]上可微。

证明 由定理2可知，F(x,y)的两个偏导分别为

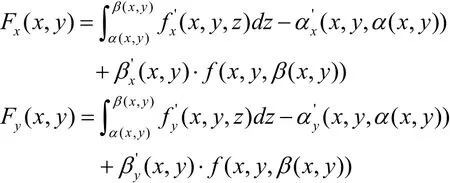
结合定理1，可知Fx(x,y)和Fy(x,y)的右端均是连续函数，即 Fx(x,y)和Fy(x,y)在定义域上存在且连续，再由引理1知，F(x,y)在矩形区域 D= [a,b] × [c,d ]上可微。

定理3 设函数 f( x,y,z)在区域

G ={(x, y, z) |α(x, y) ≤z ≤ β(x, y) (x, y) ∈[a, b ]×[c, d ]}上连续，其中α ( x, y) , β( x, y)为矩形区域

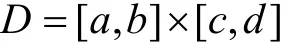
上连续函数，则函数

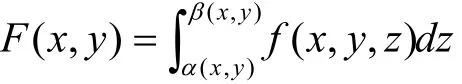
在区域 D= [a,b] × [c,d ]上可积。

证明 由定理1可知F(x,y)在 D= [a,b] × [c,d ]上连续，再结合[1]文引理1可知F(x,y)在D上可积。

从上述的证明过程可以看出，当将含参量正常积分（积分限量为函数）的被积函数推广到三元以上函数，仍可以得到如前文所述的分析性质。

3 一些实例

例1 设

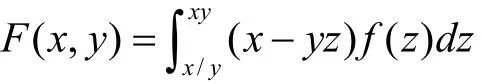
其中f(z)为可微函数，求 Fxy"(x, y)。

解 由已知条件并结合定理2知

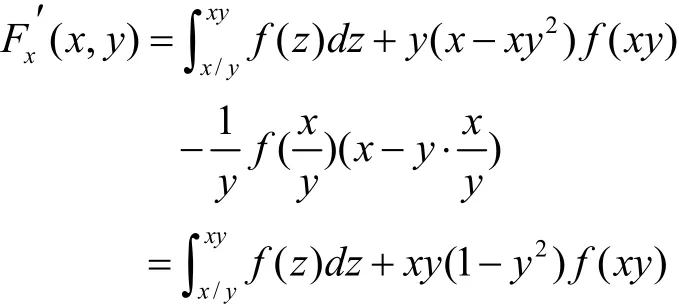
所以

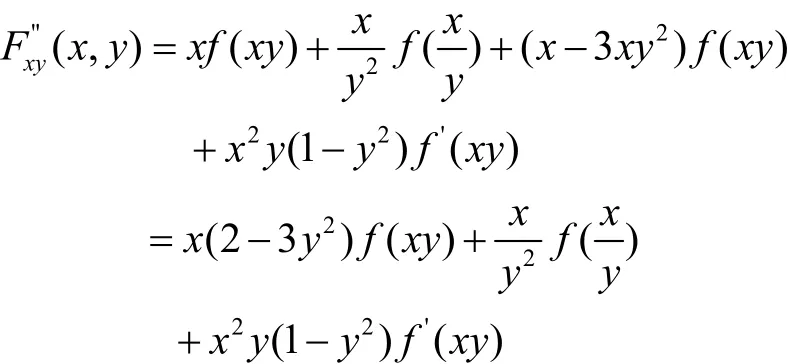
例2 设f(x)二阶可微，F(x)可微，证明：

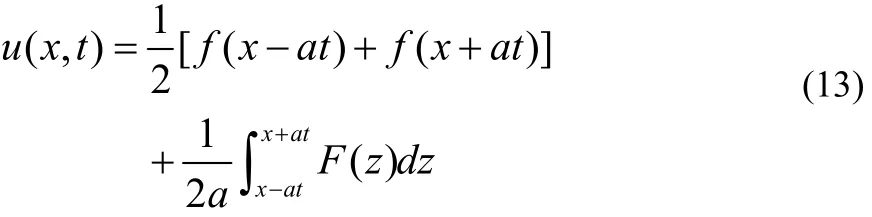
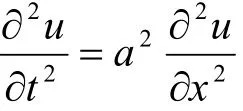
满足弦振动方程及初值条件 u( x, 0) =f( x)， ut( x, 0) =F( x)。

证明 分别对x与t应用定理4

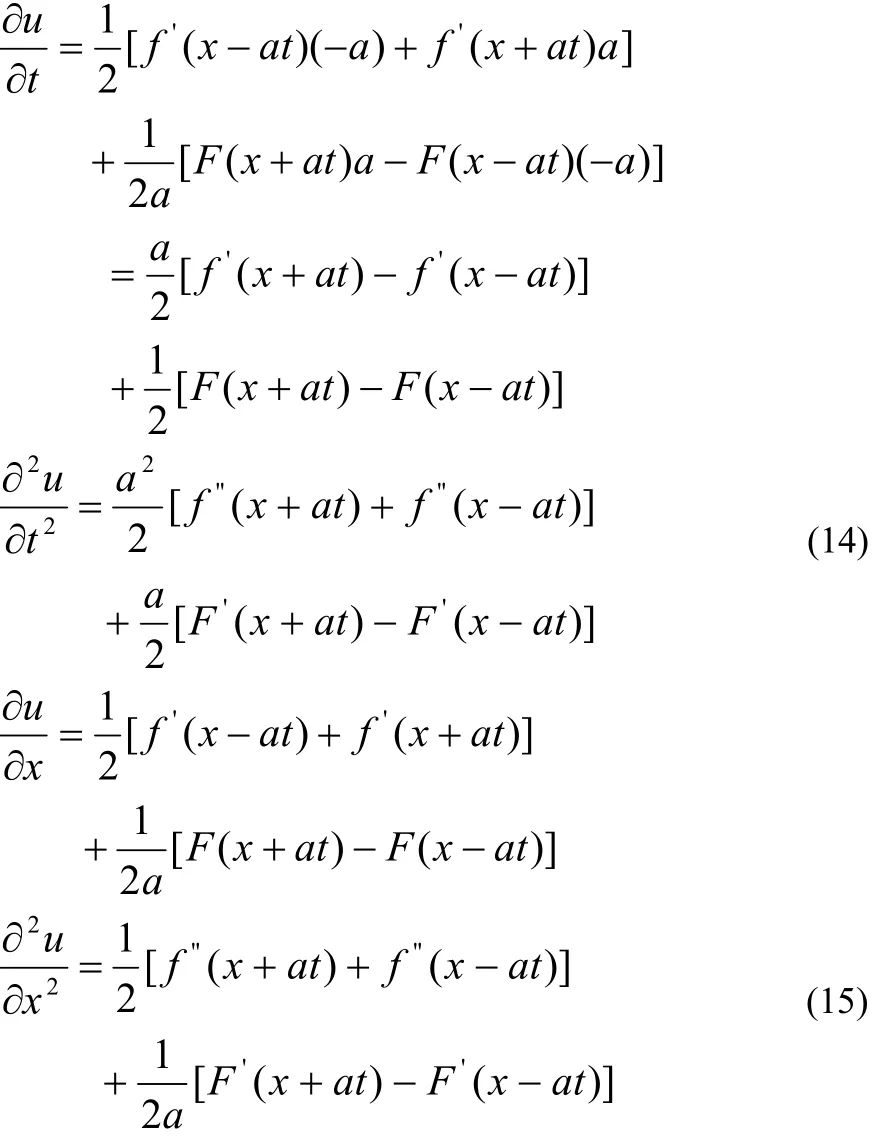
则由(14)和(15)知

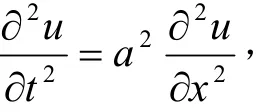
即u(x,t)是弦振动方程

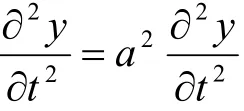
的解，且满足

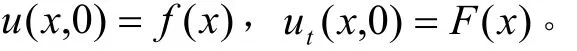
注 式(13)在偏微分方程中被称为无限长弦自由振动达朗贝尔（d’ Alembere）公式或达朗贝尔（d’ Alembere）解。

[1] 顾先明.二元含参量正常积分函数的性质[J].唐山师范学院学报,2010,32(2)：41-44.

[2] 华东师范大学数学系.数学分析[M].北京：高等教育出版社,2006.

[3] 陈纪修等.数学分析[M].北京：高等教育出版社,2004.

[4] 常庚哲,史济怀.数学分析教程[M].北京：高等教育出版社, 2003.

[5] 张筑生.数学分析新讲[M].北京：北京出版社,2009.

（责任编辑、校对：赵光峰）

Analysis Characteristic of the Second Type of Normal Integral Function with Binary Parameter

GU Xian-ming

(Department of Mathematics and Information Science, Tangshan Teachers College, Tangshan 063000, China)

On the base of the definition of normal integral function (the case of integral limiter function), the definition and consequence of the second type with given parameters of normal integral function was carred out. It was found that, in its domain, this type of integral function was of continuity, differentiability and integrability. Some examples were given.

normal integral depending on a parameter; continuity; differentiability; integrability

唐山师范学院大学生科研立项项目

2010-04-25

顾先明（1989-），男，安徽寿县人，唐山师范学院数学与信息科学系学生，研究方向为函数论。

O172

A

1009-9115(2011)05-0022-03