级数的绝对收敛性问题

董立华

（德州学院 数学系，山东 德州 253023）

级数的绝对收敛性问题

董立华

（德州学院 数学系，山东 德州 253023）

阐述了赋范线性空间中无穷级数的收敛、绝对收敛、无条件收敛等概念之间的关系，并例证说明级数的收敛与绝对收敛、绝对收敛与无条件收敛之间不等价，但确实存在着无穷维的Fréchet空间中级数的无条件收敛与绝对收敛等价。

收敛；无条件收敛；绝对收敛

1 引言

为叙述方便起见，首先给出几个定义。

定义2[2]设X是赋范线性空间，

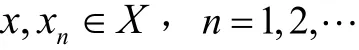
若

则称级数

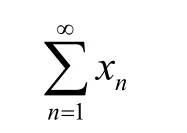
收敛于x。

定义3 赋范线性空间X中的级数

为无条件收敛，是指该级数的项在任意相互交换次序后仍旧收敛，亦即每个改换排列的级数

仍旧收敛。

定义4 级数

绝对收敛是指数项级数

收敛。

2 主要结论

限于篇幅，相关结论的证明在此省略，仅举（反）例以说明相应的逆命题不成立。

定理1 如果赋范线性空间是完备的，则该空间中绝对收敛的级数一定是收敛的。反之不成立。

例1 在Banach空间C0（C0是空间(C)中以0为极限的数列所构成的闭子空间）中考虑级数

其中

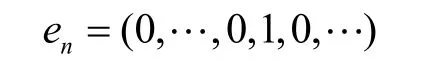
设

则x∈C0，且

故级数

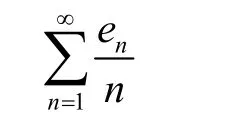
收敛于x，然而它并非绝对收敛。因为

注意 如果其中的条件“完备”不满足，则即使是绝对收敛的级数也未必收敛。

例2 在线性空间E∞上定义范数，

其中

考察级数

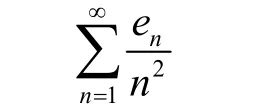
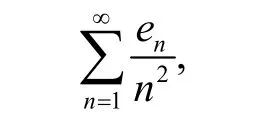
绝对收敛。另一方面，不难看出

在E∞中并不收敛。

可以进一步证明：

（1）若赋范线性空间中每个绝对收敛的级数都是收敛的，则这个空间一定是完备的。

（2）Banach空间X中的级数

无条件收敛，当且仅当每个级数

（其中ηn= 0或1）都收敛。

易知在每个有限维赋范空间中，级数的无条件收敛与绝对收敛是等价的。但在无穷维空间中有：

定理 2 Banach空间X中绝对收敛的级数一定是无条件收敛的。然而其逆不真。

Dvoretzky与Rogers已给出下面的反例。

例3 在Banach空间C[0,1]中点列{xn}如下

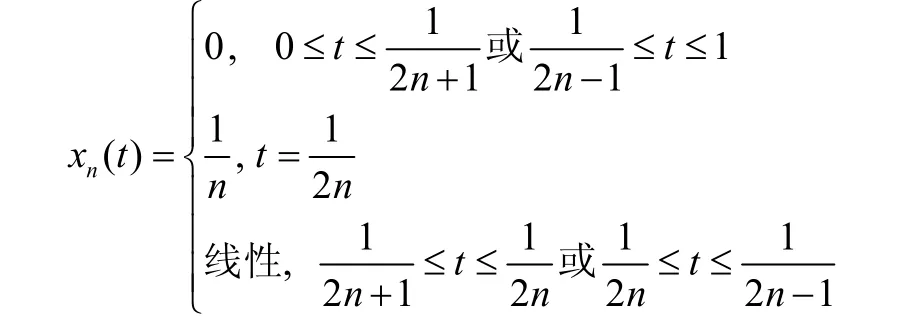
易见，函数项级数

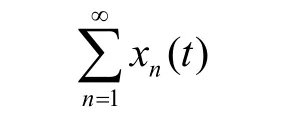
在区间[0,1]上是一致收敛的，从而对任意ε＞0，存在n0∈N+，当 p, q≥n0时，有

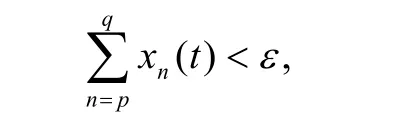
所以

因此，级数

在[0,1]中是无条件收敛的。另一方面，因为

所以

并非绝对收敛。

注意 确实存在着无穷维的Fréchet空间中级数的无条件收敛与绝对收敛等价。

现设D[0,1]是定义在区间[0,1]上的所有实值函数按通常的线性运算所成的线性空间，其中诸函数有任意阶的导数，令

此时

又令

则D[0,1]是一个Fréchet空间。由于Fréchet空间中绝对收敛的级数必是无条件收敛的，因此只需证明D[0,1]中的无条件收敛级数都是绝对收敛的。

事实上，设

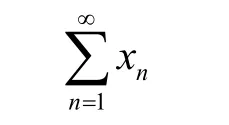
是D[0,1]内任一无条件收敛的级数，固定i，并且选择tn，使得

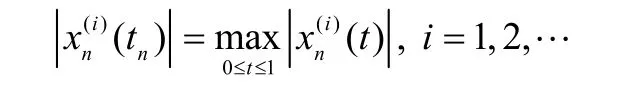
则有

因为级数

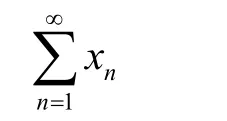
为无条件收敛的充要条件是每个级数

（其中ηn= 0或1）在D[0,1]中都收敛，而级数

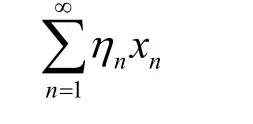
在D[0,1]中收敛等价于对每个i

在区间[0,1]上一致收敛，从而

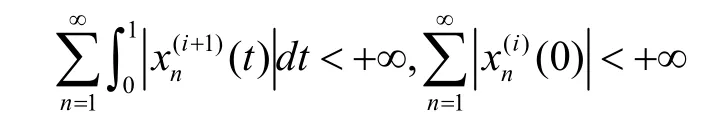
于是，由不等式（1）得到

因此，级数

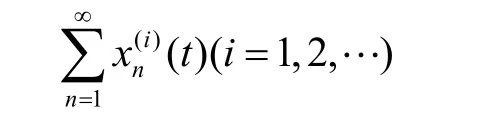
在空间C[0,1]内绝对收敛。再由空间D[0,1]中距离的定义可知，级数

在D[0,1]中绝对收敛。至于级数的无条件收敛与收敛之间的关系有下面的定理。

定理 3 Banach空间中级数的无条件收敛蕴涵着级数的收敛，反之不然。

设

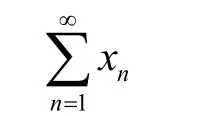
是（条件）收敛的数项级数，则根据Riemann重排定理，它可以重排而给出发散的级数，即

是收敛的，而不是无条件收敛的级数。例如级数

适当重排后，可以使之发散，即不是无条件收敛的。

综上所述，在Banach空间中一般地有：

绝对收敛⇒无条件收敛⇒收敛

但其逆命题一般不成立。

[1] 定光桂.巴拿赫空间引论[M].北京：科学出版社,1984.

[2] 汪林.泛函分析中的反例[M].北京：高等教育出版社,1994.

（责任编辑、校对：赵光峰）

The Problem on the Absolute Convergence of Series

DONG Li-hua

(Department of Mathematics, Dezhou University, Dezhou 253023, China)

This article mainly introduces the relationship between convergent series, absolutely convergent series and unconditionally convergent series in normed linear spaces. And through some counterexamples we draw the important conclusions that convergent series is unequal to absolute convergence and also the unconditional convergence is unequal to absolute convergence. This article also proves that absolute convergence is equivalent to unconditional convergence in infinite dimensional Fréchet space.

convergence; unconditional convergence; absolute convergence

山东省教育科学规划重点项目（2010JZ123）

2011-05-12

董立华（1965-），女，山东平原人，德州学院数学系教授，研究方向为泛函分析。

O177

A

1009-9115(2011)05-0009-03