错题同样值得研究

●(丹阳市教育局教研室 江苏丹阳 212300)

错题同样值得研究

●王先进(丹阳市教育局教研室 江苏丹阳 212300)

在高三数学考试中有这样一个题目：

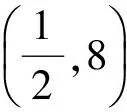
1 3种解法竟然是同一结果

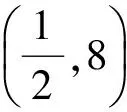
这里n-m=5,从而

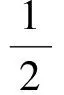
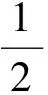
解得

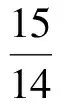
解法2图示法.若公差取得最大值，则区间内的最小项和最大项分别无限接近区间的2个端点(如图1)，此时区间内含有5d，即

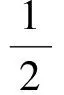
解得

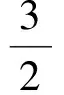
若公差取得最小值，则区间内的最小项和最大项分别离2个端点最远(1个d)，或者说最小项的前一项与最大项的后一项分别落在区间的端点处(如图2)，此时区间内含有7d，即

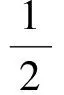
解得

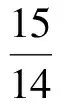
综上所述，

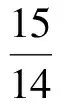
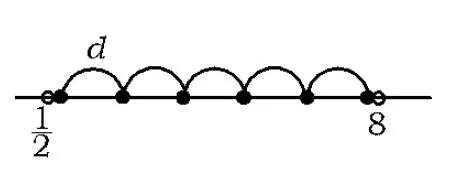
图1

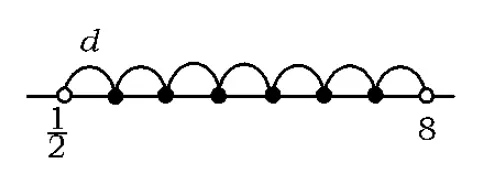
图2

解法3设落在区间内的第1项为an,则最后一项为an+5，由题意得

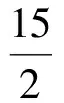
解得

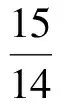
3种不同的解法，得出同一个结果，似乎应该没有什么问题了.

2 一个反例轻松推翻了结论

该题引起了一定的讨论，源于一位教师提供的反例：

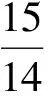
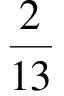
由

即

解得

2≤n≤8.

共有7项在该区间内，说明该范围不能满足题意.为什么会出现这样的情况？笔者进行了一些思考.

3 这个错误答案是如何形成的

取值范围，顾名思义，是取得到的值的集合.自然是不包括取不到的值，但也应该包括所有能取到的值，即不能多，也不能少.由本题的题意，不难理解要求的取值范围应该是前面条件的充分必要条件.

从解法1看，不等式组应该刻画的是充分必要条件，但以后的各步都只能说是充分而不必要的了，即有可能扩大了范围.

从解法2看，取最小值时，若将每项左移一点，则完全有可能出现7项在区间内，如图3所示.

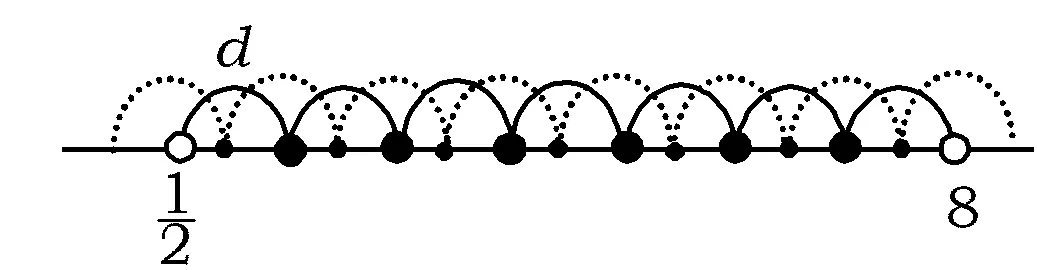
图3

看来真正的范围应该是答案的一个子集，上述反例也说明了这一点，同时也说明原答案是错误的.

如图3所示，左移一点还是右移一点与a1的值有关，而从上述的解题过程看与a1无关，这是令人难以信服的.

4 若a1是具体的值，答案是什么

作为原题的一种特殊情形，不妨先考虑以下的题目：

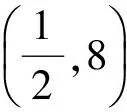
该问题的解答没有想象的简单，其思路是:先用d来表示最小项am和最大项an,再用“n-m=5”列出关于d的方程.难点在于由范围来确定项数时涉及到取整.至于是否有其他简洁解法不得而知，笔者做了多种尝试，未果.解决该问题的思路如下：

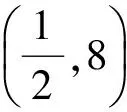
(1)用d表示最小项am.

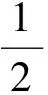
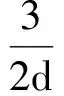
即

(2)用d表示最大项an.

由an<8,an+1≥8可得

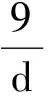
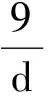
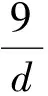
以上[x]表示的x整数部分，x≥0.

(3)列出方程.

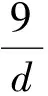
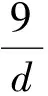
(4)解方程.

[18x]-[3x]=6.

由取整函数的性质,知

18x-1<[18x]≤18x,

-3x≤-[3x]<1-3x，

相加得

因此

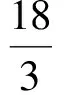
即

6≤[18x]≤8,[3x]=1，

当且仅当[18x]=7,[3x]=1时，方程(1)成立.从而

7≤18x<8,1≤3x<2，

得

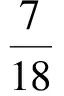
故

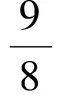
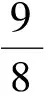
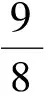
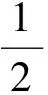
5 对这个题目的修正建议

上述解题过程中使用了取整函数.虽然取整函数的性质并不难，笔者也是在处理该问题时临时归纳出来的，但这已经超出了一般中学生的学习范围，而且考试时往往不可能也不允许有很多时间去做摸索探究.考虑到中学生知识与能力的具体情况，笔者建议作如下简化修正：

例3 已知等差数列{an}的首项a1=-1，若该数列恰有6项落在区间(-1，8)内，则公差d的取值范围为________．

这样首项与区间左端点恰好重合，落在区间内最小的一项就无需考虑，肯定是a2了，只要a7<8,a8≥8即可求出d的取值范围.这种思路的实质是，对于“恰有”、“有且只有”的某类问题，可以通过相邻2项的范围来刻画，而此思路同样可以迁移到其他题目，如：

例4 已知f(x)=sinωx+cosωx(ω>0)，若方程f(x)=0在区间[0,π]上有且只有3个解，则实数ω的取值范围是________．