6061铝合金高温流变应力方程参数反求

王 冠，李落星，刘 波，李晓青

(1. 湖南大学 汽车车身先进设计制造国家重点实验室，长沙 410082；2. 湖南大学 材料科学与工程学院，长沙 410082；3. 重庆长安汽车股份有限公司 汽车工程研究院车身技术研究所，重庆 401120)

6061铝合金高温流变应力方程参数反求

王 冠1,2，李落星1,2，刘 波3，李晓青3

(1. 湖南大学 汽车车身先进设计制造国家重点实验室，长沙 410082；2. 湖南大学 材料科学与工程学院，长沙 410082；3. 重庆长安汽车股份有限公司 汽车工程研究院车身技术研究所，重庆 401120)

结合Gleeble−1500热模拟机在变形温度为300～500 ℃，应变速率为0.01～10 s−1条件下通过等温压缩实验研究 6061铝合金的流变应力行为，采用未考虑温升效应的参数反求法及考虑温升效应的参数反求法求解流变应力方程参数，并与回归统计法得到的结果进行对比分析。结果表明：采用未考虑温升效应的参数反求法求解流变应力方程参数具有高效、准确等优点，计算峰值应力平均误差为5.17 MPa；与有限元软件结合考虑温升效应的参数反求法能够更好地描述真实的材料变形过程；3种方法得到的流变应力方程参数的偏差小于 6.28%，采用多岛遗传算法与模拟退火算法反求得到的流变应力方程参数具有较好的一致性与可靠性，参数反求法可替代传统回归统计法快速获得材料大变形条件下流变应力方程参数。

6061铝合金；参数反求；流变应力方程；热压缩变形；有限元

研究金属材料流变应力，获得准确的流变应力方程参数，有助于预测材料的变形行为及组织演化规律[1−2]。通常采用结合热模拟实验结果线性回归的方法求解流变应力方程参数。赵培峰等[3−4]根据热压缩实验数据，研究了6061铝合金热压缩变形条件对流变应力的影响，并通过一元线性回归方法，确定材料流变应力方程参数。SEMIATIN等[5]通过理论与实验手段研究了 6061铝合金在扭转实验中塑性变形生热与应变速率对局部流变应力的影响。以上工作重点在铝合金流变应力行为的研究，并未采用新方法获得铝合金的材料参数，而参数反求法可用于求解一些难以直接获得材料参数的本构模型。KARKKAINEN 等[6]对非线性数值反求方法做了细致的研究。COOREMAN等[7]采用敏度矩阵的方法反求弹塑性材料模型参数。SIMONI和 SCHREFLER[8]提出一种加速算法求解考虑约束的多层材料模型参数。ZHOU等[9]结合有限元仿真与数值优化手段反求材料参数。PONTHOT和KLEINERMANN[10]以及 GHOUATI和 GELIN[11]采用有限元软件结合反求方法求解加工成型工艺中的材料参数。但以上工作局限于小应变量变形，并未考虑到不同应变速率及变形温度对材料参数的影响，更没有涉及材料塑性功转热导致材料温度升高的现象。

本文作者通过在Gleeble−1500热模拟实验机上进行轴对称等温压缩实验，得到6061铝合金的真应力—真应变曲线，建立该合金高温变形本构方程，提出采用参数反求法求解铝合金流变应力方程参数，并与传统回归统计法对比。提出针对不同问题需要选择适当求解方法的依据，为准确预测铝合金高温流变行为提供理论支持。

1 实验

1.1 实验材料

本研究所采用的材料为半连续铸造 6061铝合金铸锭，其各元素质量分数实测值如表1所列。

6061铝合金铸锭在550 ℃保温12 h后立即室温水淬，并加工成尺寸为d 10 mm×15 mm、两端带有深0.2 mm凹槽的圆柱体轴对称样品。

表1 6061铝合金各元素质量分数Table 1 Chemical composition of 6061 aluminum alloy(mass fraction, %)

1.2 实验方法

使用Gleeble−1500热模拟机进行25组等温压缩实验，压缩温度为300、350、400、450、500 ℃，应变速率范围为 0.001、0.01、0.1、1、10 s−1，压缩率为60%，实验的升温速率为10 ℃/s，变形前保温3 min。压缩前圆柱试样两端的凹槽内填充 75%石墨+20%机油+5%硝酸(体积分数)三甲苯脂作为润滑剂，以减少摩擦对应力状态的影响。由Gleeble−1500热模拟机自动采集应力、应变、压力、位移、温度及时间等数据。

1.3 实验结果

图1所示为6061铝合金在高温等温压缩变形的真应力—真应变曲线。表2所列为6061铝合金在不同应变速率、温度条件下的实测峰值应力。通过对比可知，6061铝合金在压缩变形过程中的流变应力随变形温度的升高而减小，随变形速率的增加而增大。

图1 6061铝合金热压缩变形真应力—真应变曲线Fig.1 True stress—true strain curves of 6061 aluminum alloy by hot compression: (a) ε&=0.001 s−1; (b) ε&=10 s−1

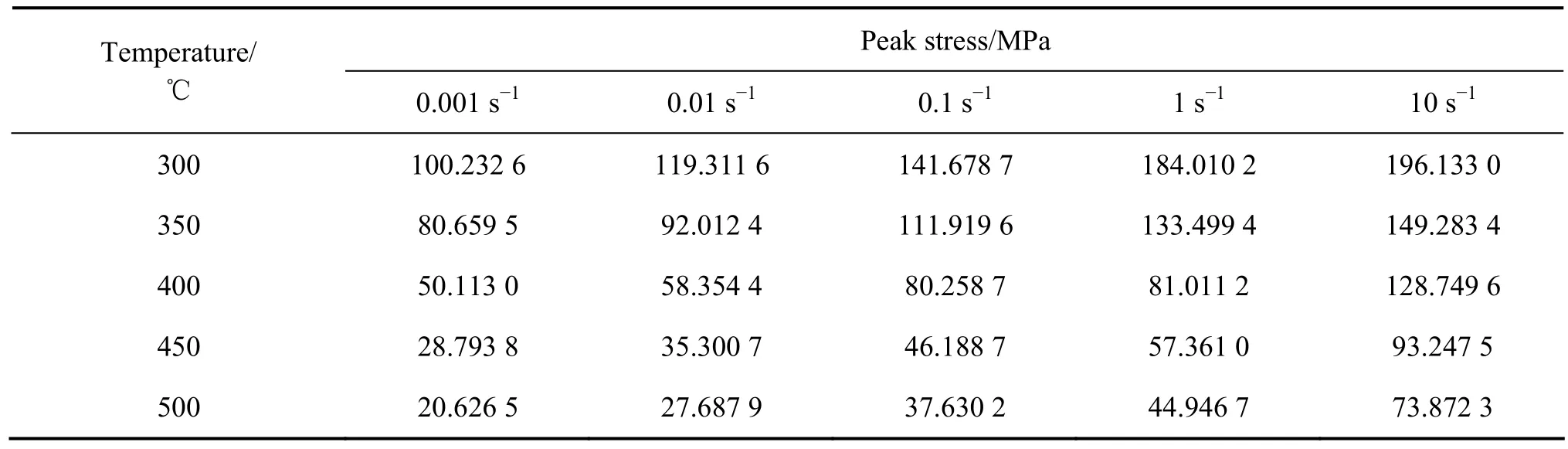
表2 不同变形条件下6061铝合金的实测峰值应力Table 2 Peak stress of 6061 aluminum alloy under different deformation conditions

2 流变应力方程参数求解

铝合金材料在热变形过程中，高温流变应力σ强烈地取决于变形温度T、应变速率ε&、变形程度ε、合金的化学成分以及变形体内显微组织结构等[2]。在常见的挤压、轧制等热加工工艺中，材料发生大变形，应变对流变应力的影响有时候是可以忽略的。ZENER和HOLLOMON[12]在已有研究的基础上提出了一种包含变形速率和变形温度的Z参数修正模型，以使材料参数的求解更准确，其物理意义为温度补偿的应变速率因子：

本研究选用Z参数修正材料本构模型，通过实验计算得到n、α、Q、A等材料参数，可利用式(2)求出材料在任意变形条件下流变应力(σ)的大小：

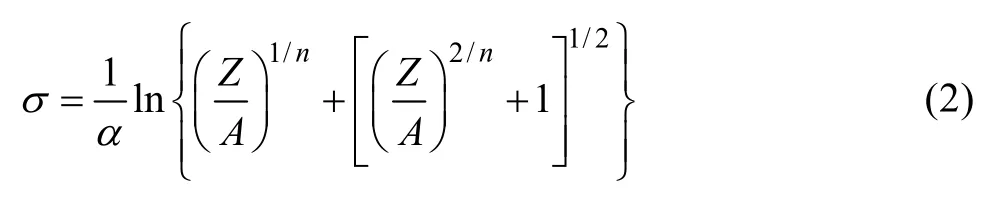
式中：n为应力指数；α为应力水平参数(mm2·N−1)；A为结构因子(s−1)；Q 为热激活能(kJ·mol−1)，是材料在热变形过程中重要的力学性能参数，反映材料热变形的难易程度；T为绝对温度(K)；R为摩尔气体常数；ε&为应变速率(s−1)。

2.1 回归统计法求解

通常可采用SELLARS等提出的双曲正弦形式描述金属材料热变形过程中的流变应力行为[13]，在不同的条件下可表示为以下3种形式：

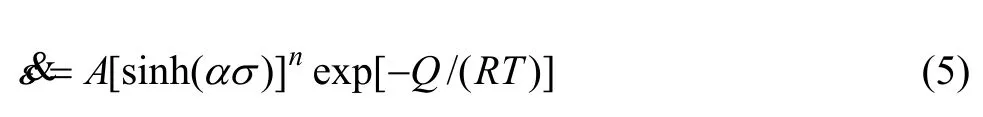
式中：n为应力指数；α为应力水平参数，满足关系α= β /n 。在低应力水平下，流变应力σ和Z之间的关系可用指数关系描述(见式(1))，而在高应力水平下可用幂指数关系描述(见式(2))，在整个应力水平下可用双曲函数关系描述(见式(3))。

引入温度补偿的应变速率因子Zener-Hollomon参数Z：

通过线性回归法可求得 6061铝合金流变应力方程中的各项材料参数见表3。

表3 线性回归法求得的6061铝合金流变应力方程参数Table 3 Constitutive parameters of 6061 aluminum alloy obtained by regression statistics method

2.2 未考虑温升效应的流变应力方程参数反求

若已知n、α、Q、A等材料参数，利用式(2)可以直接计算出在不同ε&、T条件下材料的峰值应力，因此可以采用参数反求的方法，通过不断修正流变应力方程参数，将式(2)计算出的结果与实验数据相比较，结合数值优化算法，多次迭代减小计算峰值应力与实测峰值应力的误差，最终获得高精度的流变应力方程。图2所示为未考虑温升效应的流变应力方程参数反求的流程图。

使用回归统计法求解流变应力方程参数，由于采用近似拟合的方法，需要反复作图与回归计算，求解效率与计算精度均较低，而流变应力方程参数反求法，能够在整个计算过程中完全脱离人工操作，从而一定程度上减少人为因素产生的误差。反求采用多岛遗传算法能够在计算中能够保持解的多样性，提高包含全局最优解的机会，可以抑制早熟现象的发生，具有求解效率高、计算结果准确等优点[14]。

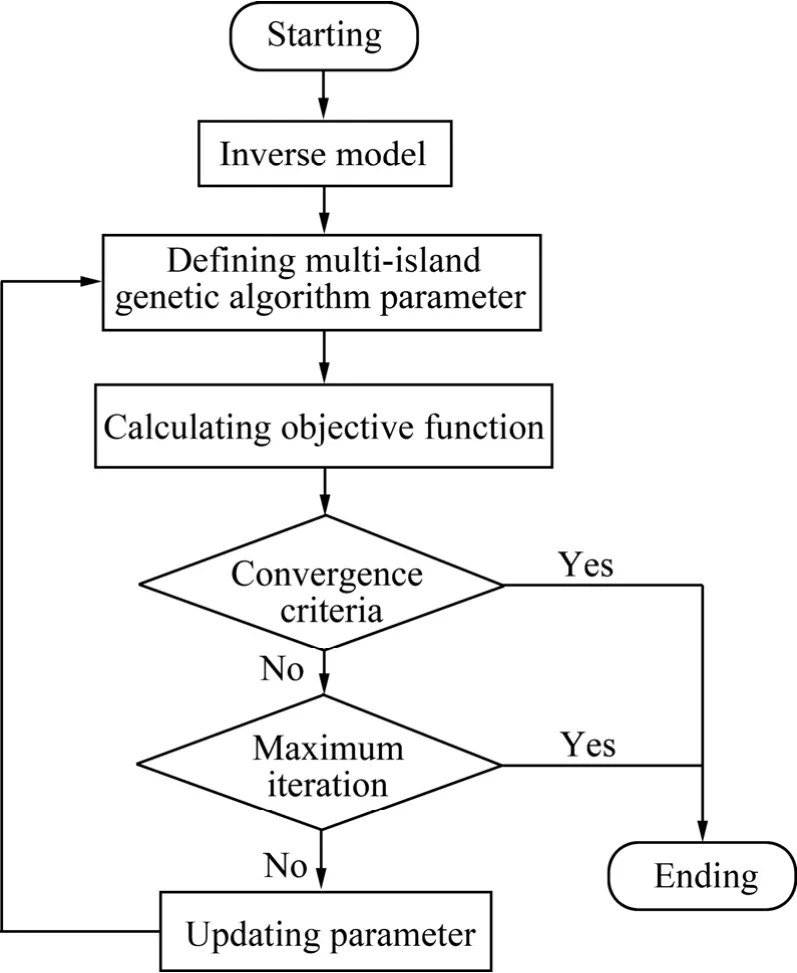
图2 流变应力方程参数反求流程图Fig.2 Flow chart of inverse method for material parameters identif i cation

在反求计算中，参数n、α、Q、A为设计变量，为保证解的多样性，尽可能增大各变量范围，定义5＜n＜9，0.01＜α＜0.02，0＜Q＜5.0×105，1.0×1017＜A＜1.0×1018。优化结果接近问题解的程度由适应度函数评定，即为目标函数。反求采用多岛遗传算法优化目标函数，通过多次迭代使目标函数收敛到最小值。在参数n、α、Q、A共同影响下，适应度函数f(n, α, Q, A)可表示如下：

采用多岛遗传算法为获得全局最优解，需要较多的迭代次数，但由于计算过程中仅需要完成方程组的求解，每次迭代时间较短，因此总体计算效率较高。图3所示为采用多岛遗传算法目标函数收敛曲线。由图3可知，参数反求前期目标函数波动较大，但随着迭代次数的增加，目标函数收敛，函数值变化趋于平缓，并最终稳定。

图3 多岛遗传算法目标函数收敛曲线Fig.3 Multi-island genetic algorithm objective function convergence curve

通过参数反求最终确定 6061铝合金流变应力方程中的各项材料参数见表4。

图4所示为回归统计法与未考虑温升效应的参数反求法得到的 6061铝合金计算峰值应力与实验数据的误差分析。其中斜线背景为式(2)求解得到的峰值应力与实验结果误差的绝对值。通过数据对比可以看出，回归统计法绝对误差在 300～400 ℃条件下较大，在450～500 ℃条件下相对减小，但存在波动；未考虑温升效应的参数反求法在300～400 ℃条件下绝对误差明显小于回归统计法，在450～500 ℃条件下绝对误差波动较大，在25组实验中有21组，参数反求法绝对误差小于回归统计法。通过计算，回归统计法平均误差14.24 MPa，未考虑温升效应的参数反求法平均误差5.18 MPa。因此，通过参数反求法得到的流变应力方程参数较回归统计法在计算峰值应力时精度更高。

综上所述，未考虑温升效应的参数反求法求解材料流变应力方程参数操作流程短，方法简单，求解精度高，计算速度快，是替代传统回归统计法求解材料参数的重要手段。

表4 参数反求法获得的6061铝合金流变应力方程参数Table 4 Constitutive parameters of 6061 aluminum alloy obtained by inverse method

图4 不同材料本构求解方法的峰值应力的绝对误差Fig.4 Absolute error of peak stress with different methods of constitutive parameters identification: (a) Regression statistics method; (b) Inverse method

2.3 考虑温升效应的流变应力方程参数反求

材料高温压缩流变应力与变形温度、变形速率和变形程度有着密切的关系。同时，在材料变形过程中，机械能一部分转化为变形热能，一部分储存于位错、空位等缺陷中。变形热能的存在导致实际变形温度升高，从而影响真应力—真应变曲线。

表5所列为热压缩实验中不同变形条件下试样的温升。由表5可知，变形温度越低，变形速率越高，引起的温升越大，从而导致应力下降越多。其中材料在变形温度为300 ℃，变形速率为10 s−1时，温升达到了50 ℃，因此，考虑温升效应对获得材料的真实力学性能极其重要。

由于峰值应力通常出现在应变较小时刻，不考虑温升效应的影响，采用基于求解流变应力方程的参数反求方法计算出的力和位移曲线，仅在峰值应力出现前精度较高，随着变形量的增加，变形抗力迅速增大，与实验结果误差较大。传统参数反求法无法考虑材料温升效应对流变应力方程参数的影响，在应用该流变应力方程参数模拟真实材料加工问题时，计算精度较低，无法真实的反映大变形过程中材料的应力状态。

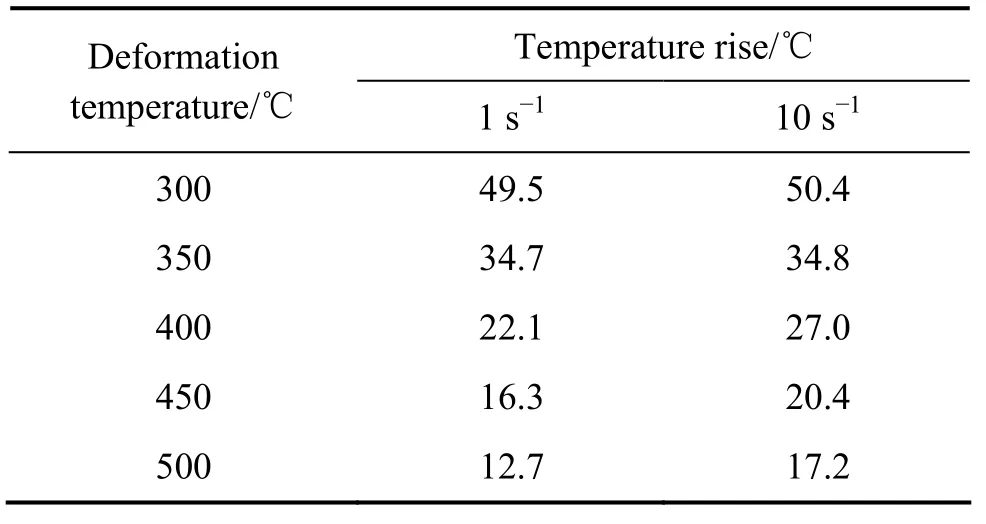
表5 6061铝合金真应变为0.94时不同变形条件下的温升Table 5 Temperature rise of 6061 aluminum alloy under different deformation conditions with true strain of 0.94

本文作者采用LS-DYNA非线性有限元软件仿真热压缩实验过程，材料本构方程使用 MAT_102双曲线模型，为提高计算效率采用隐式算法求解，并考虑变形过程中的温升效应，塑性功转化为内能的比例为90%。与热模拟实验条件相对应，建立25组仿真模型，对比每一组仿真模型与实验获得的力和位移曲线，通过不断的调整参数 n、α、Q、A，使仿真结果与实验值吻合，从而获得准确的流变应力方程参数。

图5所示为结合有限元软件考虑温升效应的参数反求流程图。在考虑温升效应的反求计算中，参数n、α、Q、A为设计变量，定义其变化范围5＜n＜9，0.01＜α＜0.02，2.0×105＜Q＜2.8×105，1.0×1017＜A＜1.0×1018。在参数n、α、Q、A共同影响下，适应度函数f(n, α, Q, A)可表示如下：

式中：N为实验次数；S为热模拟实验试样总压缩变形量；s为热模拟实验试样变形量；(s)为第i组实验测得的力和位移曲线；(n, α , Q , A, s )为仿真得到的第i组实验条件下参数为n、α、Q、A、s的力和位移曲线。

反求采用模拟退火法(SA)，可获得较快的收敛速度，同时能够获得全局解[15]。由于每次迭代均需要运行25组仿真模型，计算时间较长。图6所示为反求过程中目标函数收敛曲线。由图6可知，反求前期参数优化效率较高，目标函数值迅速下降，随着迭代次数的增加目标函数变化较慢，目标函数在1007次迭代后收敛，最终确定6061铝合金本构方程中的各项材料参数见表6。

图5 考虑温升效应的流变应力方程参数反求流程图Fig.5 Flow chart of FE based inverse method for material parameters identif i cation

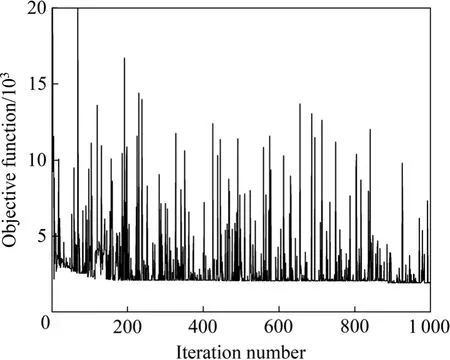
图6 模拟退火法目标函数收敛曲线Fig.6 SA algorithm objective function convergence curve

表6 考虑温升效应的参数反求法获得的6061铝合金流变应力方程参数Table 6 Constitutive parameters of 6061 aluminum alloy obtained by FE based inverse method

由表5可知，材料在变形温度为300 ℃，变形速率为10 s−1时温升效应最为显著。图7所示为该条件下力和位移曲线(实线为实验结果，虚线为仿真结果)。由图7可知，未考虑温升效应的参数反求法计算出的流变应力方程参数对于预测材料变形初期抗力较为准确，但随着变形量的增大，误差逐渐增大。而采用考虑温升效应的参数反求法计算出的力和位移曲线与实验结果吻合较好，更有利于准确预测大变形过程中材料的变形行为。

因此，针对不同问题的需要，应该选择适当的参数求解方法，以获得准确的铝合金流变应力方程参数，提高分析精度。通过分析得到，当仅研究材料峰值应力时，不需要考虑温升效应的影响，采用基于求解流变应力方程的参数反求方法计算得到的精度和效率较高；当模拟真实材料加工问题时，由于问题常伴随大变形、高温升等因素的影响，采用与有限元软件结合考虑温升效应的参数反求法能够准确描述材料的变形行为。

3 讨论

图7 6061铝合金热压缩过程的应力—位移曲线Fig.7 Force—displacement curves of 6061 aluminum alloy: (a) Inverse method; (b) FE based inverse method

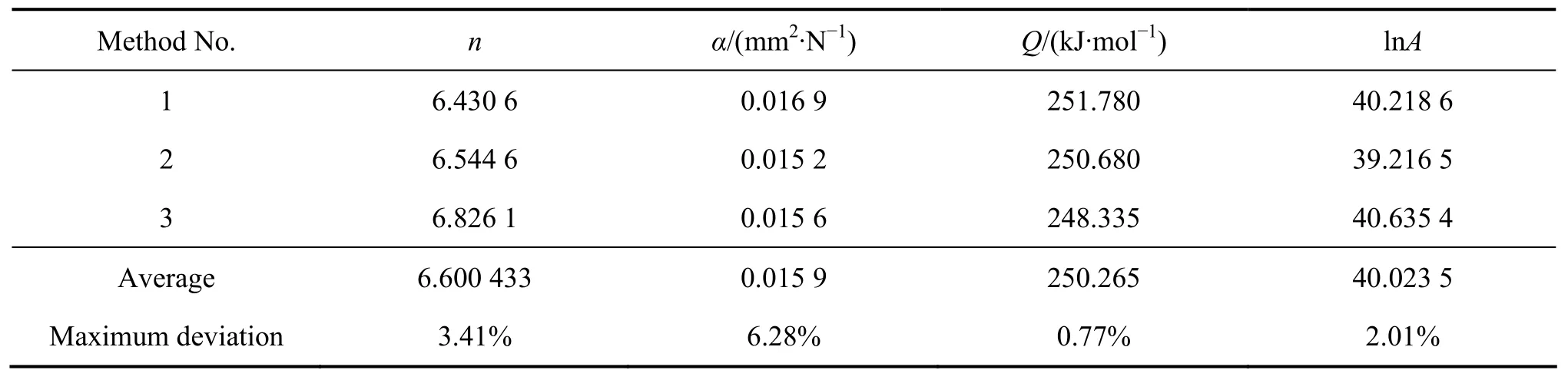
表7 6061铝合金流变应力方程参数偏差Table 7 Deviation of constitutive parameters of 6061 aluminum alloy

表7所列为6061铝合金流变应力方程参数偏差分析。表中方法1、方法2和方法3分别为回归统计法、未考虑温升效应的参数反求法和考虑温升效应的参数反求法。通过计算可知，3种方法得到的流变应力方程参数与其平均值相比偏差较小，其中参数α偏差为6.28%，参数Q偏差仅为0.77%。因此，采用回归统计法与反求法求解流变应力方程参数具有较好的一致性，能够获得可靠的材料参数。在应对具体问题时，可根据不同需求采用不同的参数求解方法，以获得较高精度的材料参数。

在求解铝合金流变应力方程参数时，其数学模型可表示为带约束的函数优化问题，具有多约束和多混合变量等特点，且由于问题的非凸性，往往存在多个局部解，传统基于梯度的数值优化算法，需要对函数求导，易收敛于局部解，不适于全局优化问题的求解。应选用模拟退火法、遗传算法等全局最优化算法，以获得更为准确、稳定且具有鲁棒性的材料参数。其中遗传算法通过模拟生物的遗传和进化，能够求解高度非线性及不连续问题，并能从整个可行解空间寻找全局最优解和次优解，但该算法需要较多的迭代次数，计算量较大。模拟退火法在迭代后期目标函数收敛较慢，局部寻优能力不足。因此，可以采用模拟退火法获得精度较低的全局最优解后，继续通过基于梯度的优化算法寻找高精度的局部最优解，从而高效、准确地获得问题的全局最优解。

在反求过程中，材料参数作为优化变量，其变化范围对计算有较大影响，不适当的变量范围会导致反求计算终止。同时，增大材料参数变量的变化范围，并不会影响到最优解的稳定性。例如材料参数Q，设置变量范围0～5.0×105与 2.0×105～2.8×105反求得到的结果相同，因此，应增大材料参数的变化范围，以获得更加全面的最优解，但增大变量范围，会增加求解时间、降低计算效率。

4 结论

1) 通过未考虑温升效应的参数反求法得到 6061铝合金高温流变应力方程参数A、α和n的值分别为39.216 5 s−1、0.015 2 mm2/N 和 6.544 6，其中变形激活能Q为250.680 kJ/mol。

2) 采用回归统计法求解流变应力方程参数可以获得较为准确的结果，计算峰值应力平均误差 14.24 MPa，但操作复杂、效率较低；通过反求流变应力方程参数可以获得较回归统计法更准确的结果，计算峰值应力平均误差5.27 MPa，且计算效率高，操作简便。

3) 当仅研究材料峰值应力时，采用基于求解流变应力方程不考虑温升效应的参数反求方法计算精度较高；当模拟真实材料加工问题时，采用与有限元软件结合考虑温升效应的参数反求法能够准确描述材料的变形行为。

4) 通过回归统计法与反求法得到的流变应力方程参数n、α、Q和lnA的偏差均小于6.28%，具有较好的一致性与可靠性。

REFERENCES

[1] 王祝堂, 田荣璋. 铝合金及其加工手册[M]. 长沙: 中南大学出版社, 2005: 251−262.WANG Zhu-tang, TIAN Rong-zhang. Aluminum alloy and processing manual[M]. Central South University Press, 2005:251−262.

[2] 寇琳媛, 金能萍, 张 辉, 韩 逸, 吴文祥, 李落星. 7150铝合金高温热压缩变形流变应力行为[J]. 塑性工程学报, 2010,20(1): 43−48.KOU Lin-yuan，JIN Neng-ping, ZHANG Hui, HAN Yi, WU Wen-xiang, LI Luo-xing. Flow stress behavior of 7150 aluminum alloy during hot compression deformation at elevated temperature[J]. Transactions of Nonferrous Metals Society of China, 2010, 20(1): 43−48.

[3] 赵培峰, 任广升, 徐春国, 沈 智. 6061铝合金材料常数的研究[J]. 塑性工程学报, 2006, 13(4): 79−81.ZHAO Pei-feng, REN Guang-sheng, XU Chun-guo, SHEN Zhi.Research on material constant values of 6061 Aluminum alloy[J].Journal of Plasticity Engineering, 2006, 13(4): 79−81.

[4] 赵培峰, 任广升, 沈 智, 徐春国. 6061铝合金热压缩变形条件对流变应力的影响及其本构方程的研究[J]. 塑性工程学报,2007, 14(6): 130−133.ZHAO Pei-feng, REN Guang-sheng, SHEN Zhi, XU Chun-guo.Influence of hot compressive deformation conditions of 6061 aluminum alloy on flow stress and research on its constitutive equation[J]. Journal of Plasticity Engineering, 2007, 14(6):130−133.

[5] SEMIATIN S L, FREY N, WALKER N D, JONAS J J. Effect of deformation heating and strain rate sensitivity on flow localization during the torsion testing of 6061 aluminum[J]. Acta Metallurgica, 1986, 34(1): 167−176.

[6] KARKKAINEN T, NEITTAANMAKI P, NIEMISTO A.Numerical method for nonlinear inverse problem[J]. Journal of Computational and Applied Mathematics, 1996, 74(1): 231−244.

[7] COOREMAN S, LECOMPTE D, SOL H, VANTOMME J,DEBRUYNE D. Elasto-plastic material parameter identification by inverse methods: Calculation of the sensitivity matrix[J].International Journal of Solids and Structures, 2007, 44(13):4329−4341.

[8] SIMONI L, SCHREFLER B A. An accelerated algorithm for parameter identification in a hierarchical plasticity model accounting for material constraints[J]. International Journal for Numerical and Analytical Methods in Geomechanics, 2001,25(3): 263−272.

[9] ZHOU Ji-ming, QI Le-hua, CHEN Guo-ding. New inverse method for identification of constitutive parameters[J].Transactions of Nonferrous Metals Society of China, 2006, 16(1):148−152.

[10] PONTHOT J, KLEINERMANN J. A cascade optimization methodology for automatic parameter identification and shape/process optimization in metal forming simulation[J].Comput Methods Appl Mech Eng, 2006, 195(41/43):5472−5508.

[11] GHOUATI O, GELIN J C. Identification of material parameters directly from metal forming processes[J]. Journal of Materials Processing Technology, 1998, 80/81: 560−564.

[12] ZENER C, HOLLOMON J H. Effect of strain-rate upon the plastic flow of steel[J]. J Appl Phys, 1944, 15(1): 22−27.

[13] SHI H, MCLAREN A J, SELLARS C M, SHAHANI R,BOLINGBROKE R. Constitutive equations for high temperature flow stress of aluminum alloys[J]. Mater Sci Eng, 1997, 13(3):210−216.

[14] BABBAR M, MINSKER B S. Multiscale island injection genetic algorithms for groundwater remediation[J]. Advances in Water Resources, 2007, 30(9): 1933−1942.

[15] CORANA A, MARHESI M, MARTINI C, RIDELLA S.Minimizing multimodal functions of continuous variables with the simulated annealing algorithm[J]. ACM Transactions on Mathematical Software, 1987, 13(3): 262−280.

Constitutive parameters identification of 6061 aluminum alloy during hot deformation with inverse methods

WANG Guan1,2, LI Luo-xing1,2, LIU Bo3, LI Xiao-qing3
(1. State Key Laboratory of Advanced Design and Manufacture for Vehicle Body,Hunan University, Changsha 410082, China;2. College of Materials Science and Engineering, Hunan University, Changsha 410082, China;3. Automotive Engineering Institute Body Technology Research Department,Chongqing Chang’an Automobile Co. Ltd., Chongqing 401120, China)

The flow stress behaviors of 6061 aluminum alloy were studied by compression test at the deformation temperature of 300−450 ℃ and strain rate of 0.01−10 s−1on Gleeble−1500 system. With the experimental data, the material parameters for the hot deformation constitutive equation were obtained by inverse methods and finite element(FE) simulation based on the inverse methods and compared with the results obtained by regression statistics methods.The results show that the inverse method is efficient and accurate. The average error of flow stress of 6061 aluminum alloy is 5.17 MPa with the inverse methods. The constitutive parameters identified with FE based inverse methods can accurately describe the hot compression deformation of 6061 aluminum alloy. The deviation of constructive parameters obtained by inverse methods, FE based inverse methods and regression statistics methods is less than 6.28%. The constitutive parameters obtained by multi-island genetic algorithm and simulated annealing (SA) algorithm are reliable and robust. Under the large deformation condition, the reverse methods can substitute the traditional regression statistic methods to identify the constitutive parameters accurately and efficiently.

6061 aluminum alloy; inverse method; flow stress equation; hot compression deformation; finite element method

TG 146.21

A

1004-0609(2011)12-3011-08

国家自然科学基金面上项目(51075132)；高等学校博士学科点专项科研基金资助项目(20090161110027)；湖南省杰出青年基金资助项目(09JJ1007)；湖南大学汽车车身先进设计制造国家重点实验室自主课题(61075005)

2010-11-19；

2011-03-09

李落星，教授，博士；电话：0731-88821950；E-mail: luoxing_li@yahoo.com

(编辑 李艳红)