高等数学课程改革研究＊

赵坚

(大同煤炭职业技术学院，山西大同037003)

高等数学课程改革研究＊

赵坚

(大同煤炭职业技术学院，山西大同037003)

针对高职院校课程改革过程中，高等数学课程遇到的问题和困难，研究高等数学课程及其专业课程的相互关系，着重分析研究在教学过程中需要解决的问题。力图使高等数学的教学，能够更好地适应高职院校发展与教学的需要。

高等数学;专业课;改革;教学

针对在专业课的教学过程中，可能出现的数学问题以及所需要的数学知识，特别通过专业课程里的习题，资料的收集、整理和研究，研究其使用的数学知识和方法，以期指导教学工作，提高教师的教学能力，促进学生的学习兴趣。

在研究初期，我们计划的研究目标是高等数学知识在一线的工作环境中的具体应用，但经过和专家的交流，集体讨论分析之后觉得，一方面我们缺乏实际操作的条件，无法进行验证。另一方面，除了相关的技术研究人员以外，一线的工作人员，更多需要的是实践知识和能力，而不是高等数学的理论知识。因此，将研究工作的重点，放在高等数学在专业教学中的学习里，具体说就是对专业课教学的研究，搞清楚专业课程可能需要的数学知识或者是数学知识在专业课程里的应用。我们认为，现在已经基本取得了一定的成果，但是也可以在以后继续进行研究，不断丰富其内容。

目前所做的工作，只是对采矿系一些专业的研究，具体的内容集中在《矿山岩体力学》以及《矿井通风》两门课程上。

例如:在《矿井通风》课程中，要讲述矿井通风动力时，会涉及到自然风压的形成及特性。是说风流从气温较低的井筒进入矿井，从气温较高的井筒流出。在正在开凿的立井井筒中，冬季风流会沿井筒中心一带进入井下，而沿井壁流出井外;夏季风流方向正好相反。这是由于空气温度与井筒围岩温度存在差异，空气与围岩进行热交换，造成进风井筒与回风井筒、井筒中心一带与井壁附近空气存在温度差，气温低处的空气密度比气温高处的空气密度大，使得不同地方的相同高度空气柱重量不等，从而使风流发生流动，形成了自然通风现象。因此把这个空气柱的重量差称为自然风压H自。如图1。

如果把地表大气视为一个断面无限大、风阻为零的假想风路，则可将通风系统视为一个有高差的闭合回路，由自然风压的形成原因，可得到其计算公式:

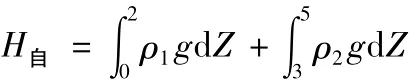
式中:H自为矿井的自然风压，Pa;Z为矿井最高点到最低点间的距离，m;g为重力加速度，m/s2;ρ1和ρ2为分别为0－1－2和5－4－3井巷中dZ段空气密度，kg/m3。

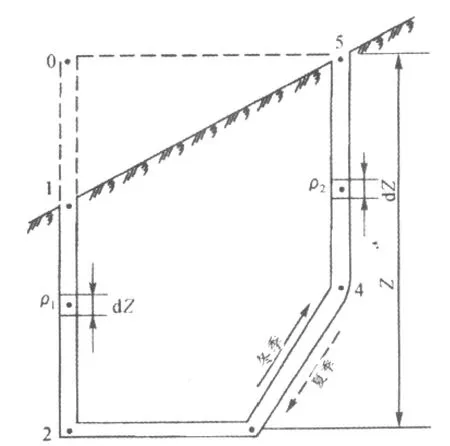
图1 简化矿井通风系统

这个公式，其实就是高等数学中一个简单的定积分的计算。由积分号、积分上下限、被积表达式、积分变量组成。

在高等数学的教学过程里，当讲授这部分知识的同时，就可以告诉学生，在实际工作可能会有应用，比如通风专业使用的这个公式。这样做，很自然就能够调动起学生的学习热情。在学习专业课程时，也会很容易想起数学课堂上的学习情景。对于两门课程，有互相促进的效果。

在《矿山岩体力学》里，我们也找到了涉及高数公式的身影。比如剪应变和转动表达式:而这就是高数里面有关复合函数偏导数的内容。

通过对上诉例题的研究和分析，可以发现，一般情况下，高等数学在专业课程中的应用，都是比较简单的。针对我院学生理论底子比较差的情况，相应的降低教学知识的教学和考核难度，以够用为度。这样的做法，可以提高学生的学习积极性，也为教学改革研究提供了一条思路。

但对于那些基础较好，有专升本要求的学生，也要注意区别对待，不要一味降低难度，挫伤其学习的积极性。

但是这其中又存在一个问题，我们对不同的系部，讲述高数的内容是不同的，主要是因为各个专业的专业课设置的安排和课时不相同。机电类的授课时间是一学年，而采矿系的一些专业是一学期，按照通常的做法，我们就会删减讲授内容。比如对于采矿系的专业，只讲授前几章内容。针对讲授的内容，我们也做过一些调整，一般课本，会把微分方程部分安排在多元函数求导部分之后讲授。而考虑到连续性和教学内容的合理性，就把微分方程这一部分安排在了定积分之后进行讲授，其余部分，就不做讲授，要不然，教学任务就无法完成。

但通过对专业课程教材的研究发现，以前对教学内容所做的安排，太简单，只是根据时间与课时的要求，把教材一分为二，一学期的讲一半，一学年的讲全书。而在矿山岩体力学中，有关高数的内容，主要会用到的，其实正是我们不讲授的内容，比如，多元函数偏导数和高阶求导的内容。

那么，在以后的教学过程中，就可以做出一些相应的调整，一方面要降低难度，删减内容;一方面，还要添加内容，把专业课程需要的知识，加入到我们的讲授内容里。

但面临的问题，又不是一方面努力就能解决的，相关专业的课程内容安排，也不合理。比如，在物理学里，第一章就有二阶导数的内容，而在高数教学里，这一部分，起码会在第二章才能出现。

这就要做一个解释了，因为有些人认为，可以把其他专业课需要的知识提前来讲授，但他们可能不了解，高数是一个严谨，具有联系性的课程。前面的知识没有讲授，后面的教学就无法进行。以前我们对教学内容的调整，也是在考虑前后知识衔接的情况下做出的。

所以，只能在降低难度、删减内容与添加内容上来做文章了。就是前面所说的，以够用为度，对每一章有难度的部分，作为学生自学内容，留给基础较好的同学，满足他们的需要，教师可以给予辅导。这样就可以提高讲授速度，以弥补其他学科对教学内容的提前需要。而所增加的内容，也是在严格按照教学计划的前提下，把一些在专业课教学里需要的高数知识进行讲授，当然，前提也是，够用为度。

那么具体的讲授内容，在此不能体现出来的，只提供一个思路。在今后的教学里，我们将根据这一思路，组织教研室的成员，统一部署，逐章讨论，尽可能合理地组织教学。

也有人提出类似模块化的教学模式，就是需要哪里讲哪里。但高数是如此严谨，连续性是无法回避的问题。就像我们做出的研究内容里提到的，在专业课程里，可能需要的高数知识并不多，比如:多元函数高阶求导和偏导数，但是前面的基础教学却一点也不能少，否则，教学根本不能进行下去了，“毛之不存，皮将焉附”，空中楼阁是不现实的。当然，我们也可以对于模块化的情况做一些研究，也一定会对我们的教学工作有所帮助。

我们所做的研究还略显稚嫩，内容不多，却颇费周章。说明我们的教学研究能力还有欠缺，理论知识与实际工作有脱节。这是我们今后要注意和研究的一个方面。

在以后的教学研究中，我们可以继续加大加深研究的内容和专业领域。真正做到教学中的教学相长。学生在学习不同课程中融会贯通，教师在研究中互通有无。提高学院的学术水平，扩大学院的学习氛围。

［1］雷化南．矿山岩体力学［M］．北京:冶金工业出版社，1983．

［2］周茂增．矿井通风［M］．北京:煤炭工业出版社，1993．

［3］赵文茹．高等数学(理工科)［M］．北京:北京交通大学出版社，2009．

2011－08－02

赵坚(1972－)，男，河北衡水人，讲师。