分歧泊松自回归模型的马尔可夫性
2011-11-26孙耀东
孙耀东
(吉林师范大学数学学院,中国 四平 136000)
Powell[1]在20世纪五六十年代做了大量的细菌细胞分裂试验,其研究的细胞分裂过程如下:初始状态由一个母细胞分裂为两个子细胞,之后每一代子细胞都各自分裂为两个下一代子细胞,如记母细胞为X1,则X1分裂为X2和X3,之后X2分裂为X4和X5,X3分裂为X6和X7,以此类推.通过对试验数据分析,子细胞受遗传和环境因素影响,由同一个细胞分裂出来的两个子细胞由于其生长环境接近,环境对它们的影响具有相关性.针对此特点,Cowan与Staudte[2]在经典的自相关模型AR(1)基础上提出分歧自回归模型BAR(1).文献[3~5]进一步分析细胞分裂过程将分歧自回归模型理论不断发展完善,Huggins与Basawa[6]提出分歧ARMA(p,q)模型,Huggins与Basawa[7]讨论了高斯型分歧AR(p)模型,得到了参数的极大似然估计,Basawa与Zhou[8]讨论了非高斯型分歧自回归模型,Zhou与Basawa[9]给出了指数型分歧自回归模型的极大似然估计.
Zhou与Basawa[10]提出分歧泊松模型,模型形式如下:
(1)
其中,Yi,i=1,2,…,为独立同分布随机序列,共同分布为二项分布B(φ1),参数φ1∈(0,1),{(ε2,ε3),(ε4,ε5),(ε6,ε7),…}为独立同分布二维随机序列,表示环境对细胞分裂的影响,其共同分布是
y∧z=min(y,z),参数λ>0,μ>0.
下面主要讨论模型(1)的性质.
1 分歧泊松自回归模型的性质
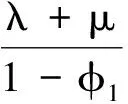
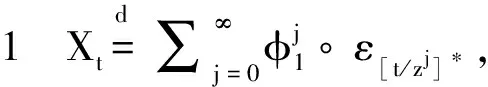
证记φt(s),ψ(s)分别为Xt和εt的母函数,|s|≤1.将X1之前的细胞记为X0、X-1、X-2、…,那么(1)可表示成
由引理1的证明有
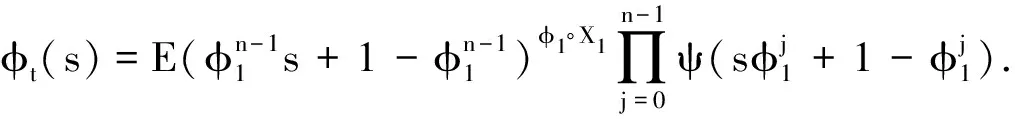
(2)
令X-∞=Y,对(2)反复迭代有
可以得出

(3)
考虑(3)式第一项
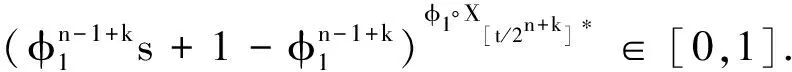

(4)
其中Yi,i=1,2,…,为独立同分布随机序列,共同分布为二项分布B(φ1j).
2 分歧泊松自回归模型的马尔可夫性
定理2任意一条由细胞及其一个子细胞构成的细胞分裂链是不可约常返马尔可夫链,如X1,X2,X4,….
证不妨取{X2t|t=0,1,2,…},下面证明它是一条不可约常返马尔可夫链.考虑下面模型:
X2t=φ1∘X2t-1+ε2t,t=1,2,….
(5)
对任意的t≥1及非负整数i1,i2,…,it+1,
P(X2t+1=it+1|X1=i1,X2=i2,…,X2t=it)=P(X2t+1=it+1|X2t=it),
所以{X2t|t=0,1,2,…}是马尔可夫链.记P(ε2t=i)=f(i)>0,i=0,1,…,状态i到j的转移概率为Pij,有
所以{X2t|t=0,1,2,…}不可约.
下面证明其常返性.对于(5)式反复迭代有


下面先证明
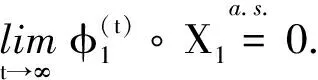
(6)
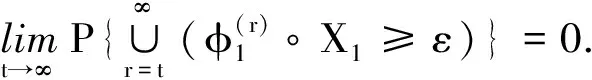
从而(6)式成立.

由于ε2t-i与X1是独立的,所以

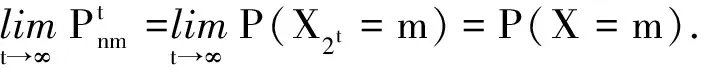

参考文献:
[1] POWELL E O. Some fearures of the generation times of individual bacteria[J].Biometrika,1955,42(1-2):16-44.
[2] COWAN R, STAUDTE R G. The bifurcating autoregression model in cell lineage studies[J].Biometrika,1986,42(4):769-783.
[3] STAUDTE R G. A bifurcating autoregression model for cell lineage data with varying generation means[J].J Theor Biol,1992,156(2):183-195.
[4] HUGGINS R M, STAUDTE R G. Variance components models for dependent cell populations[J].J Am Stat Assoc,1994,89(425):19-29.
[5] HUGGINS R M. Robust inference for variance components models for single trees of cell lineage data[J].Ann Stat,1996,24(3):1145-1160.
[6] HUGGINS R M, BASAWA I V. Extensions of the bifurcating autoregressive model for cell lineage studies[J].J Appl Probab,1999,36(4):1225-1233.
[7] HUGGINS R M, BASAWA I V. Inference for the extended bifurcating autoregressive model for cell lineage studies[J].Aust & New Zealand J Stat,2000,42(4):423-432.
[8] BASAWA I V, ZHOU J. Non-Gaussian bifurcating models and quasi-likelihood estimation[J]. J Appl Probab,2004,41(1):55-64.
[9] ZHOU J, BASAWA I V. Maximum likelihood estimation for a first-order bifurcating autoregressive process with exponential errors[J].J Time Ser Anal,2005,26(6):825-842.
[10] ZHOU J, BASAWA I V. Least-squares estimation for bifurcating autoregressive processes[J].Stat & Probab Lett,2005,74(1):77-88.
[11] 孙耀东,宋立新.分歧泊松自回归横型的渐近分布[J].廊坊师范学院学报,2009,9(2):24-25.
