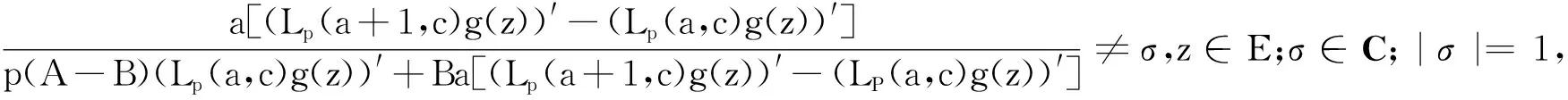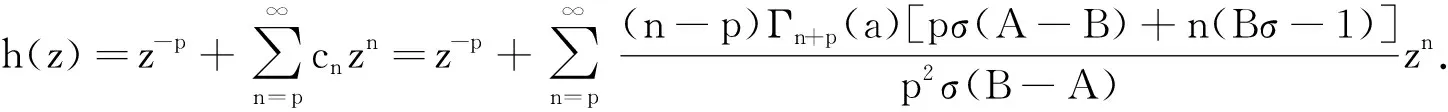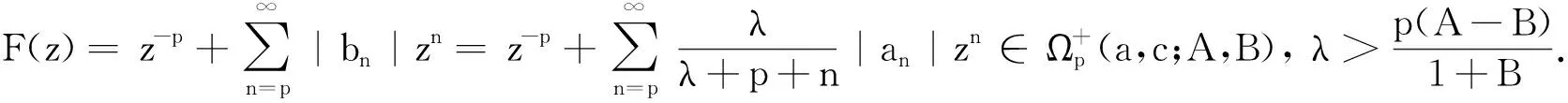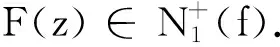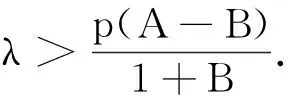基于Lp(a,c)算子定义的亚纯函数邻域的性质
2011-11-24周伟
周 伟
(淮阴师范学院数学科学学院,中国 淮安 223300)
近年来,基于不同的线性算子,有关p叶解析或亚纯函数类的性质和特征被广泛研究,请参阅文献[1~4].有学者在利用线性算子Lp(a,c)定义亚纯多叶函数的基础上,较为详尽的研究了以原点为极点的、具有正系数的亚纯函数的新子类的性质,并得出了一些新的结论[5-7].文中在利用线性算子Lp(a,c)定义亚纯函数邻域概念的基础上,进一步探究邻域与亚纯函数新子类的一些包含关系.
1 预备知识
定义1设∑P表示形如

(1)
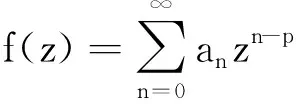

定义2设f∈∑p,关于∑p的线性算子Lp(a,c)定义如下:
Lp(a,c)f(z)=φp(a,c;z)*f(z).
易验证Lp(a,c)算子满足:

z(Lp(a,c)f(z))′=aLp(a+1,c)f(z)-(a+p)Lp(a,c)f(z).
由线性算子Lp(a,c)定义亚纯多叶函数的新子类如下.
定义3若f∈∑p且满足

(2)
其中z∈E;-1≤B (3) 定义4设f∈∑p且形如(1)式,定义f的δ邻域为 -1≤B (4) 设f∈∑p且形如(3)式,定义 0≤B (5) 为证明定理需要,给出以下引理. (6) (7) 时,结论是精确的. 以下假定a>0且c>0. 定理1设f∈Ωp(a,c;A,B),且f形如(1)式,若f满足 则Nδ(f)⊂Ωp(a,c;A,B). 证由(2)式可得g∈Ωp(a,c;A,B)当且仅当 上式等价于 (8) 其中 (9) 由(9)式可得 n,p∈N. 若δ不能再减小,则结论是精确的. 证利用和定理1相同的证明方法可证得 余下部分的证明类似于定理1的证明. 下面考虑精确性.取 (10) 由定理的假设可得 n=p,p+1,…;p∈N. 利用(4)式可得 易证常数1是最精确的. 证毕. 类似于证明定理2的方法易推证下面结论成立. 参考文献: [1] SRIVASTAVA H M, PATEL J. Some subclasses of multivalent functions involving a certain linear operator[J].J Math Anal Appl, 2005, 310(1):209-228. [2] NOOR K I. Some classes ofp-valent analytic functions defiened by certain integral operator [J]. Appl Math Comput, 2004,157(3):835-840. [3] LIU J L, SRIVASTAVA H M. Subclasses of meromorphically multivalent functions associated with a certain linear operator[J].Math Comput Modelling, 2004, 39(1):35-44. [4] LIU J L, SRIVASTAVA H M. Classes of meromorphically multivalent functions associated with the generalized hypergeometeic function[J].Math Comput Modelling, 2004, 39(1):21-34. [5] GOEL R M, SOHI N S. A new criteron forp-valent functions[J]. Proc Amer Math Soc, 1980,78(3):353-357. [6] 韦 叶,陈建兰,刘金林.由线性算子定义的一类p叶解析函数[J].扬州大学学报, 2006, 9(1):5-8. [7] 杨定恭.由线性算子定义的解析多叶函数类[J].常熟理工学院学报, 2006, 20(4):9-14. [8] 程艳莉,刘金林.一个线性算子及其相关的亚纯多叶函数类[J].扬州大学学报,2004, 7(2):10-12. [9] LIU J L. On a subclass of meromorphicp-valent functions defined by certain linear operator [J]. J Math, 2001, 21(3):276-280. [10] 程艳莉.具有正系数的亚纯p叶函数的一个子类[J].甘肃联合大学学报,2004,18(3):16-19.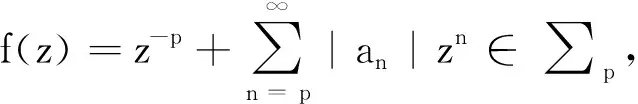
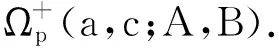

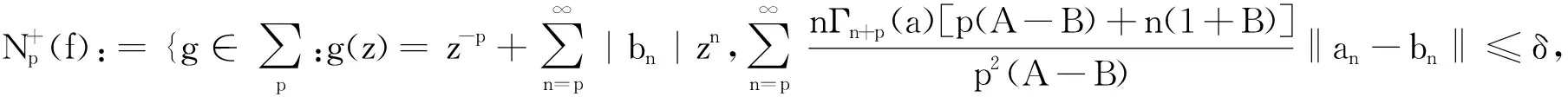
2 相关引理
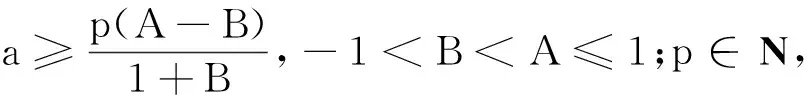




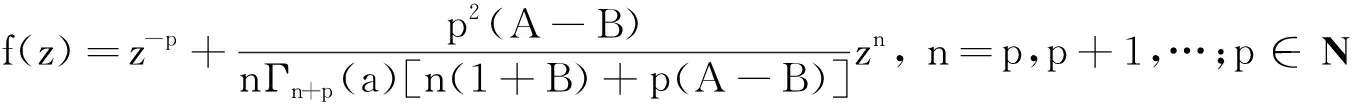
3 主要结论及证明