一类四阶抛物型方程的初边值问题

李文清 , 张能伟

(1.郑州大学 数学系,河南 郑州 450052; 2.河南工程学院 数理科学系,河南 郑州 451191;3.安阳师范学院 数学与统计学院,河南 安阳 455002)

Kdv方程已成为数学物理的基本方程之一，有关的研究十分活跃.1972年，Benjamin,Bona和Mahony在水波研究时提出了BBM方程[1]

ut-uxxt+ux+uux=0，

(1)

并断言这是比Kdv方程更合适的数学物理方程.方程(1)是作为Kdv方程的精确解提出的[2]，文献[3]讨论了具有耗散项的一维广义BBM-Burgers方程ut+f(u)x-αuxxt-βuxx+γuxxxx=0.文献[4]研究了BBM-Burgers方程ut-uxxt-αuxx+ux+uux=0解的衰减.

对于小初值问题，在文献[5]和文献[6]中,作者讨论了一维广义BBM方程ut-uxxt+ux+upux=0的解的衰减估计，在文献[7]中作者研究了下列广义BBM-Burgers方程的初值问题

的解的存在性.

而本文研究如下四阶线性抛物型方程的初边值问题

的整体广义解.

在此文中，我们分别记‖·‖LP(Ω)(1≤p≤∞)和‖·‖Hk(Ω)(k为非负整数)为‖·‖p与‖·‖Hk，特别地，‖·‖=‖·‖2，Ω=(0，1).

1 问题(2)～(4)整体广义解的存在唯一性

设{yn(x)}是下列常微分方程特征值问题

对于特征值λn(n=1，2，…)的特征函数构成L2(Ω)空间的标准正交基 .

(5)

(6)

方程(5)和初始条件(6)分别乘以ys(x)并在Ω上积分

(7)

(8)

由Levay-Schaulder不动点原理和常微分理论可以得到初值问题(7)、(8)在[0，T]上存在解αN，s(t)∈C′[0，T].

将(7)式乘以αN，s(t)，对s=1，2，…，N求和得

(uNt，uN)-(uNxxt，uN)-(uNxx，uN)+(uNxxxx，uN)=(F，uN)，

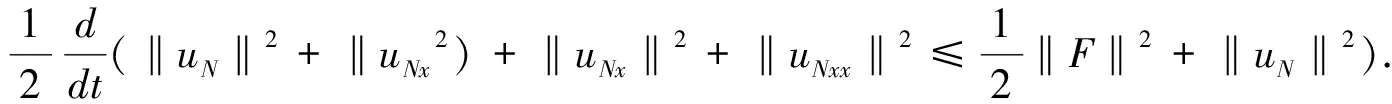
由Gronwall不等式得

(9)

(uNt，uNx4)-(uNxxt，uNx4)-(uNxx，uNx4)+(uNxxxx，uNx7)=(F，uNx4),

由Gronwall不等式得

(10)

将(7)式乘以-λsαN，s(t)，对s=1，2，…，N求和得

-(uNt，uNx2t)+(uNx2t，uNx2t)+(uNxx，uNx2t)-(uNx4，uNx2t)=-(F，uNx2t)，

由Gronwall不等式得

(11)

所以由(9)、(10)、(11)得

(12)

并且uN∈C([0，T]，H4(Ω))，uNt∈C([0，T]，H2(Ω))，利用Sobolev嵌入定理知：

故由弱紧性定理可得，问题(2)～(4)存在唯一整体广义解

u(x，t)∈C([0，T)，H3)∩L2([0，T)，H4)ut∈L2([0，T)，H2)且

故有以下定理 .

定理设u0(x)∈H3(Ω)，F(x，t)∈L2(QT),则问题(2)～(4)存在唯一整体广义解u(x，t)∈C([0，T]，H3(Ω))∩L2([0，T]，H4(Ω))，ut∈L2([0，T]，H2(Ω)),且有估计

其中，C1(T)是依赖T的非减函数，QT=Ω×(0，T).

参考文献：

[1] Benjam T B,Bona J L,Mahony J J.Model equations for long waves in nonlinear dispersive systems[J].Philosophical Transactions of Royal Society ，1972(272)：47-78.

[2] Medeiros L A, Perla M G.Existence and uniqueness for periodic solutions of the Benjamin-Bona-Mahong equation[J].SIAM Journal on Mathematical Analysis，1977(8)：792-799.

[3] Zhao H，Admas R A.Existence and convergence of solutions for the generalized BBM-Burgers equations with dissipative term II: the multidimensional case[J].Applicable Analysis，2000，75(1/2)：107-135.

[4] Albert J.Dispersion of low energy waves for the generalized Benjamin-Bona-Mahong equation[J].Journal of Differential Equations，1986(63)：111-134.

[5] Biler P.Long time behavior of solutions of the generalized Benjamin-Bona-Mahong equation in two space dimensions[J].Differential and Integral Equations, 1992(5)：891-901.

[6] Albert J.On the decay of solutions of the generalized Benjamin-Bona-Mahong equation[J].Mathematical Analysis and Applications,1989(63)：527-538.

[7] Zhao H.Optimal temporal decay estimate for the solution to the multidimensional generalized BBM-Burgers equations with dissipative term[J].Applicable Analysis ,2000,75(1/2)：85-105.