On Square Matrices with Stable Entries

CHEN Huan-yin

(College of Science, Hangzhou Normal University, Hangzhou 310036, China)

On Square Matrices with Stable Entries

CHEN Huan-yin

(College of Science, Hangzhou Normal University, Hangzhou 310036, China)

This paper extended stable rings to ideals of a ring, and investigated matrices with stable entries.The results prove that every square matrix with 1-stable entries over an exchange ring admits a diagonal reduction, and that every square matrix with unit 1-stable entries is a sum of two invertible matrices.The paper obtained an analogous result by square matrices with 2-stable entries, and studied triangular decompositions of square matrices with stable entries.

1-stable ideal; unit 1-stable ideal; 2-stable ideal; square matrix

1 Introduction

A square matrixAover a ringRis called to admit a diagonal reduction if there exist invertible matricesPandQsuch thatPAQis a diagonal matrix.It is well known that every square matrix over unit-regular rings admits a diagonal reduction(cf.[11, Theorem 3]).P.Ara et al.have extended this result to separative exchange rings (cf.[2, Theorem 2.4]).On the other hand, Menal and Moncasi(1982) showed that the diagonalizability for some rectangular matrix over some regular rings fails.In this paper, we show that every square matrix with 1-stable entries over an exchange ring admits a diagonal reduction.A ringRis said to be a (s,2)-ring in case every element inRis a sum of two units.We know that ifRis a (s,2)-ring, then so isMn(R), i.e., every square matrix over a (s,2)-ring is generated by two invertible matrices.A natural problem is how to extend this fact to matrices over a ring which is not a (s,2)-ring.It is proved that every square matrix with unit 1-stable entries is generated by two invertible matrices.Furthermore, we get a analogous result for matrices with 2-stable entries.Triangular decompositions of square matrices with stable entries are also studied.

2 Stable Range One

An idealIof a ringRis said to have stable range one ifaR+bR=Rwitha∈1+I,b∈Rimplies that there existsy∈Rsuch thata+by∈U(R).Vaserstein proved that an idealIhaving stable range one depends only on the ring structure ofI, and not on the ambient ringR.In other words,Ias an ideal of a ringRhas stable range one if and only ifIas a non-unital ring has stable range one.We say that an elementx∈Ris 1-stable in caseRxRhas stable range one.Clearly, every element in an ideal having stable range one is 1-stable.Also we note that the sum and the product of two 1-stable elements of a ring is 1-stable.In [12], one proved that there is a unique largest idealR0of a ringRwhich has stable range one, namely, the sum of all ideals having stable range one.We now derive the following.

Lemma1 LetRbe a ring, and letA∈Mn(R).Then the following are equivalent:

(1) Every entry ofAis 1-stable.

(2)A∈Mn(R0).

(3)Mn(R)AMn(R) has stable range one.

Proof(1)⟹(2) is trivial.

(2)⟹(3) SinceA=(aij)∈Mn(R0), we getMn(R)AMn(R)⊆Mn(R0) as ideals ofMn(R).This infers thatMn(R)AMn(R) as an ideal ofMn(R) has stable range one, and soMn(R)AMn(R) as a non-unital ring has stable range one.

Recall that an elementx∈Ris regular provided that there existsy∈Rsuch thatx=xyx.A ring is said to be regular in case every element inRis regular.IfRis a regular ring, we note thatR0coincides with the ideal generalized by all idempotents ofRwhose corner is unit-regular(see [12, Lemma 1.5]).

Lemma2 LetIbe an ideal of a ringR,a,b∈Ibe regular.IfIhas stable range one, then the following hold:

(1)aR=bRimplies thata=bufor au∈U(R).

(2)Ra=Rbimplies thata=ubfor au∈U(R).

ProofObvious.

Lemma3 LetIbe an ideal of a ringR.IfIhas stable range one, thenaR≅bRwith regulara,b∈Iimplies thata=ubvfor someu,v∈U(R).

ProofClear.

Theorem1 LetRbe an exchange ring,A∈Mn(R) be regular.If every entry ofAis 1-stable, thenAadmits a diagonal reduction.

LetIbe an ideal of a ringR.We setGL2(I)=GL2(R)∩(I2+M2(I)).

Lemma4 LetIbe an ideal of a ringR,A∈GL2(I).IfIhas stable range one, then the following hold:

(1)A=[*,*]B21(*)B12(*)B21(y) for ay∈R.

(2)A=[*,*]B12(*)B21(*)B12(y) for ay∈R.

(2) SinceIhas stable range one, so hasIop.Applying (1) to (A-1)op, we complete the proof.

Theorem2 LetRbe a ring,A∈GL2(R).If every entry ofI2-Ais 1-stable, then the following hold:

(1)A=[*,*]B21(*)B12(*)B21(y) for ay∈R.

(2)A=[*,*]B12(*)B21(*)B12(y) for ay∈R.

(a) Ifα=1,β=1, thenx=1,y=2.

(b) Ifα=1,β=-1, thenx=-1,y=2.

(c) Ifα=-1,β=1, thenx=1,y=-2.

(d) Ifα=-1,β=-1, thenx=-1,y=-2.

In any case, 1+xy≠0.ThereforeAcan not be written in the form (1) overZ.

3 Unit 1-Stable Ideals

In [8, Lemma 2.1], the first author proved that a ringRsatisfies unit 1-stable if and only ifax+b=1 witha,x,b∈Rimplies that there exists ay∈Rsuch thata+by,1-xy∈U(R).Now we extend unit 1-stable range condition as follows.

Definition1 We say that an idealIof a ringRis unit 1-stable provided thatax+b=1 witha∈1+I,x,b∈Rimplies that there existsy∈Rsuch thata+by,1-xy∈U(R).

Clearly, every unit 1-stable ideal of a ring is 1-stable, and that every ideal of a ring satisfying unit 1-stable range is unit 1-stable.LetR=Z/2Z⊕Z/3ZandI=0⊕Z/3Z.ThenIis unitI-stable as an ideal ofR, whileRdoesn’t satisfies unit 1-stable range.Thus the concept of unit 1-stable ideal is a nontrivial generalization of unit 1-stable range condition.We say that an elementx∈Ris unit 1-stable in caseRxRas an ideal ofRis unit 1-stable.One easily checks that a ringRsatisfies unit 1-stable range if and only if every element inRis unit 1-stable.Also we see that every element in the Jacobson radical of a ring is unit 1-stable.

Theorem3 LetIbe an ideal of a ringR.Then the following are equivalent:

(1)Iis unit 1-stable.

(2) For anyx∈1+I,y∈R, there existsu∈U(R) such that 1+(x-u)y∈U(R).

(3) For anyx∈1+I,y∈R, there existsa∈Rsuch thatx+a,1+ya∈U(R).

(4) Wheneverax+b=1 witha∈1+I,x,b∈R, there existsu∈U(R) such thatx+ub∈U(R).

Proof(1)⟹(4) Givenax+b=1 witha∈1+I,x,b∈R, then we havey∈Rsuch thata+by=u,1-xy=v∈U(R).So we get

Thereforex+vu-1b∈U(R).

(4)⟹(2) For anyx∈1+I,y∈R, we havex(-y)+(1+xy)=1.So we get someu∈U(R) such that-y+u(1+xy)∈U(R); hence, 1+(x-u-1)y∈U(R), as required.

(2)⟹(3) For anyx∈1+I,y∈R, we haveu∈U(R) such that 1+(x-u)(-y)∈U(R).Leta=u-x.Thenx+a,1+ay∈U(R).Furthermore, we have 1+ya∈U(R).

(3)⟹(1) Suppose thatax+b=1 witha∈1+I,x,b∈R.Then we havec∈Rsuch thata+(-c)=u,1+(-c)x=v∈U(R).Thus we getb+ux=1-(a-u)x=v∈U(R).This implies that

Clearly,a-bv-1u(u-1a-1)∈U(R).Sety=v-1u(1-u-1a).Thena+by,1-xy∈U(R), as asserted.

Corollary1 LetIbe an ideal of a ringR.IfIis unit 1-stable, then so isMn(I) as an ideal ofMn(R).

ProofIt is clear.

Corollary2 LetIbe an ideal of a ringR.IfIis unit 1-stable, then every square matrix overIis a sum of two invertible matrices.

ProofIt is obvious.

LetTMn(R) be the ring of alln×nlower triangular matrices overR, and letTMn(I) be the ideal of alln×nlower triangular matrices overI.We can derive the following.

Theorem4 LetIbe an ideal of a ringR.Then the following are equivalent:

(1)Ias an ideal ofRis unit 1-stable.

(2)TMn(I) as an ideal ofTMn(R) is unit 1-stable.

ProofIt suffices to show that the result holds forn=2.Assume thatIas an ideal ofRis unit 1-stable.By a directly verification, we obtain the result.

There is an analogous result for the ring of upper triangular matrices overRand the ideal of upper triangular matrices overI.Also we note that Theorem 4 can not be generalized matrix rings.For example,M2(Z/2Z) is unit 1-stable as an ideal ofM2(Z/2Z), whileZ/2Zis not unit 1-stable as an ideal ofZ/2Z.

4 Unit 1-Stable Entries

By virtue of Theorem 1, we know that every square regular matrix with unit 1-stable entries over an exchange ring admits a diagonal reduction.In this section, we investigate further properties of such square matrices.

Lemma5 IfIandJare unit 1-stable as ideals of a ringR, then so isI+J.

ProofSuppose that (1+a1+a2)x+b=1 witha1∈I,a2∈J,x,b∈R.Then (1+a1)x+(a2x+b)=1.By Theorem 3, we get someu∈U(R) such thatx+u(a2x+b)=v∈U(R).Hence (1+ua2)xv-1+ubv-1=1 with 1+ua2∈1+I.By Theorem 3 again, there existsw∈U(R) such thatxv-1+wubv-1∈U(R).Thereforex+wub∈U(R).So the result follows by Theorem 3.

Since the sum of two unit 1-stable ideals is unit 1-stable, there is a unique largest idealR*ofRwhich is unit 1-stable as an ideal ofR, namely, the sum of all unit 1-stable ideals ofR.One easily checks that every entry ofA∈Mn(R) is unit 1-stable if and only ifA∈Mn(R*).

Theorem5 Every square matrix with unit 1-stable matrices is a sum of two invertible matrices.

Corollary3 Every square matrix over a ring satisfying unit 1-stable range is a sum of two invertible matrices.

ProofObviously, every entry of a square matrix over a ring satisfying unit 1-stable range is unit 1-stable.Therefore the result follows by Theorem 5.

Lemma6 LetIbe an ideal of a ringR.Then the following are equivalent:

(1)Iis unit 1-stable.

(2) Wheneverax+b=1 withx∈1+I,a,b∈R, there existsu∈U(R) such thata+bu∈U(R).

ProofSince 1+cd∈U(R) if and only if 1+dc∈U(R) for anyc,d∈R, by Theorem 3, we see thatIis unit 1-stable as an ideal ofRif and only if so isIopas an ideal of the opposite ringRop.Therefore we complete the proof from Theorem 3.

Lemma7 LetIbe a unit 1-stable ideal of a ringR.WheneveraR+bR=Rwitha∈1+I,b∈I, there existsu∈U(R) such thata+bu∈U(R).

ProofObvious.

Lemma8 LetIbe a unit 1-stable ideal of a ringR,A∈GLn(I).Then the following hold:

(1)A=[*,*]B21(*)B12(*)B21(u) for au∈U(R).

(2)A=[*,*]B12(*)B21(*)B12(u) for au∈U(R).

(2) AsIis a unit 1-stable ideal of a ringR, so isIopas an ideal ofR.LetA∈GLn(I).Then ((A-1)op)T∈GLn(Iop).Applying (1) toRop, we have auop∈U(Rop) such that ((A-1)op)T=[*op,*op]B21(*op)B12(*op)B21(-uop).ThereforeA=[*,*]B12(*)B21(*)B12(u), as asserted.

Theorem6 LetA∈GLn(R).Suppose that every entry ofI2-Ais unit 1-stable.Then the following hold:

(1)A=[*,*]B21(*)B12(*)B21(u) for au∈U(R).

(2)A=[*,*]B12(*)B21(*)B12(u) for au∈U(R).

5 2-Fold Stable Ideals

LetIbe an ideal of a ringR.We say thatIis a 2-fold stable ideal ofRif the following holds:

We say that an elementx∈Ris 2-fold stable incaseRxRas an ideal ofRis 2-fold stable.We know that every unit 1-stable element is 1-stable, and that every 2-fold stable element is unit 1-stable.

Lemma9 LetRbe a ring, and lete∈Rbe an idempotent.IfIis 2-fold stable as an ideal ofR, theneIeis 2-fold stable as an ideal ofeRe.

Lemma10 IfIandJare 2-fold stable as ideals of a ringR, then so isI+J.

Theorem7 LetRbe a ring,A∈Mn(R).Then the following are equivalent:

(1) Every entry ofAis 2-fold stable.

(2) There exists a 2-fold stable idealIofRsuch thatA∈Mn(I).

(2)⟹(1) Suppose thatIis a 2-fold stable ideal ofRsuch thatA=(aij)∈Mn(I).Then allRaijR⊆I.AsIis 2-fold stable, we show that allRaijRare 2-fold stable as ideals ofR, as asserted.

6 2-Fold Stable Entries

In this section, we investigate square matrices with 2-fold stable entries over a regular ring.

Lemma11 LetIbe a 2-fold stable ideal of a ring, and lete∈Ibe an idempotent.TheneReis a 2-fold stable ring.

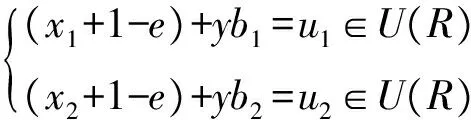
The following result is well known, we omit its proof.

Lemma12 LetIbe an ideal of a regular ringRandx1,x2,…,xm∈I.Then there exists an idempotente∈Isuch thatxi∈eRefor alli=1,2,…,m.

Lemma13 LetIbe a 2-stable ideal of a regular ringR, and letA1,A2∈GLn(I).Then the following hold:

overeRewhereeα1e,eβ1e,eα2e,eβ2e∈U(eRe).This infers that

(1) diag(1-e,1-e)+diag(e,e)A1diag(e,e)=[eα1e+1-e,eβ1e+1-e]B12(ex1e)B21(ez1e)B12(eye)

(2) diag(1-e,1-e)+diag(e,e)A1diag(e,e)=[eα2e+1-e,eβ2e+1-e]B12(ex2e)B21(ez2e)B12(eye)

(2) is proved in the same manner.

Theorem8 LetRbe a regular ring,A1,A2∈GL2(R).If every entry ofI2-A1andI2-A2is 2-fold stable, then the following hold:

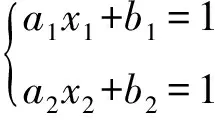
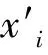
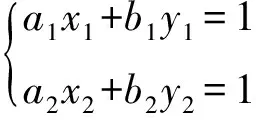
In view of Theorem 5, we see that every square matrix with 2-fold stable entries is a sum of two invertible matrices.Furthermore, we derive the following.

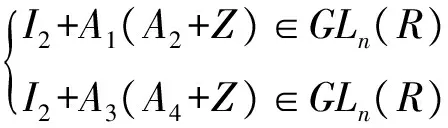
by Theorem 9, we getZ∈Mn(eRe) such that

Therefore

as asserted.

[1] Ara P.Strongly π-regular rings have stable range one[J].Proc Amer Math Soc,1996,124(11):3293-3298.

[2] Ara P, Goodearl K R, O’Meara K C,etal.Diagonalization of matrices over regular rings[J].Linear Algebra Appl,1997,265(1/2/3):147-163.

[3] Canfell M J.Completion of diagrams by automorphisms and Bass’ first stable range condition[J].J Algebra,1995,176(2):480-503.

[4] Carmona J J, Cuf J, Menal P.On the unit 1-stable rank of rings of analytic functions[J].Publ Mat Barc，1992,36(2)：439-447.

[5] Chen Huanyin.Onm-fold stable exchange rings[J].Comm Algebra,1999,27(11)：5639-5647.

[6] Chen Huanyin.Exchange rings with artinian primitive factors[J].Algebra Represent Theory,1999,2(2):201-207.

[7] Chen Huanyin.Exchange rings satisfying unit 1-stable range[J].Kyushu J Math,2000，54：1-6.

[8] Chen Huanyin.Units, idempotents and stable range conditions[J].Comm Algebra,2001,29(2)：703-717.

[9] Chen Huanyin.Extensions of rings with many units[J].Comm Algebra,2003,31(5):2403-2416.

[10] Goodearl K R, Menal P.Stable range one for rings with many units[J].J Pure Appl Algebra,1988,54：261-287.

[11] Henriksen M.On a class of regular rings that are elementary divisor rings[J].Arch Math,1973,24(1):133-141.

[12] Menal P, Moncasi J.Lifting units in self-injective rings and an index theory for RickartC*-algebras[J].Pacific J Math,1987,126(2):295-329.

[13] Vasertein L N.Stable rank of rings and dimensionality of topological spaces[J].Funct Anal Appl,1971，5(2):17-27.

[14] You Hong.K2(R,I) of unit 1-stable ring[J].Chin Sci Bull,1990,35：1590-1595.

[15] Yu Huaping.Stable range one for exchange rings[J].J Pure Appl Algebra,1995,98:105-109.

具有稳定元的方块矩阵

陈焕艮

(杭州师范大学理学院，浙江 杭州 310036)

把稳定环推广到理想上， 从而讨论了具有稳定元的方块矩阵， 得到了置换环上这类矩阵可对角化， 进一步讨论了其它相关的稳定性问题.

1-稳定理想;单位1-稳定理想；2-稳定理想；方块矩阵

date：2011-01-02

Biography：CHEN huan-yin(1963—), male, born in Xinghua, Jiangsu Province, Ph.D., Professor, majored in non-commutative algebra and K-theory.E-mail: huanyinchen@yahoo.cn

10.3969/j.issn.1674-232X.2011.04.001

O153MSC2010: 19U10ArticlecharacterA

1674-232X(2011)04-0289-09