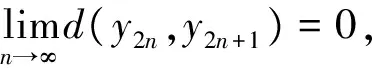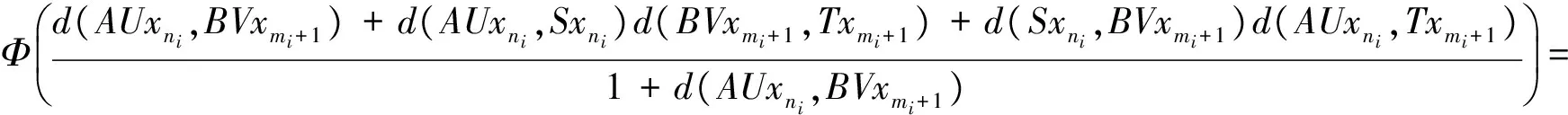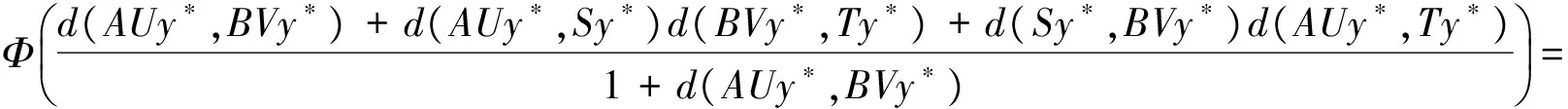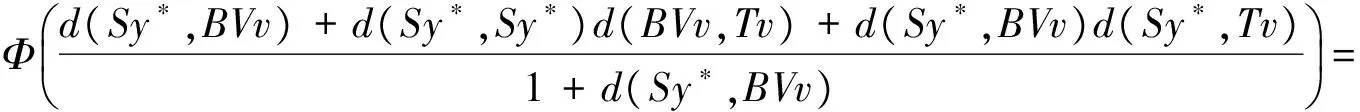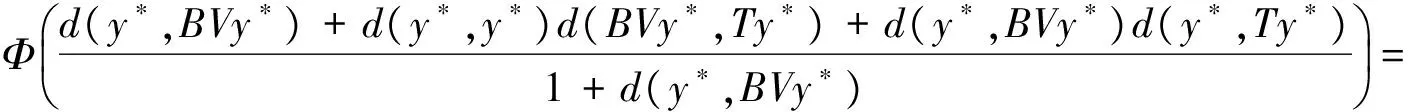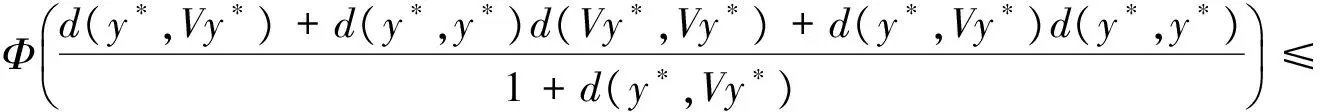关于Φ-压缩条件下六个映象的公共不动点定理

陆 竞

(杭州师范大学理学院,浙江 杭州 310036)

关于Φ-压缩条件下六个映象的公共不动点定理

陆 竞

(杭州师范大学理学院,浙江 杭州 310036)

利用度量空间中自映象对相容和次相容的条件，讨论了完备度量空间中一类Φ-压缩映象的公共不动点的存在性与唯一性，得到了几个新的公共不动点定理.

相容映象对；次相容映象对；Φ-压缩映象；公共不动点

1 引言和预备知识

众所周知，不动点理论在数学和工程数学中有着极其广泛的应用.关于公共不动点方面，张石生[1]和谷峰[2]在度量空间中利用映象对可交换和相容的条件，分别研究了两类映象的公共不动点定理问题.此后，很多公共不动点方面的理论成果不断涌现，参见文献[3-8].该文利用映象对相容[9]和次相容[10]的条件，讨论了完备度量空间中6个映象的一类新的Φ-压缩映象的公共不动点问题，获得了一个新的公共不动点定理.

定义1 集合X上的自映象对(f,g)称为是可交换的，如果∀x∈X，有fgx=gfx.

定义2[9]度量空间(X,d)上的自映象对(f,g)称为相容的，如果∀{xn}⊂X，当fxn→x，gxn→x，x∈X时，有d(fgxn,gfxn)→0(n→∞).

定义3[10]集合X上的自映象对(f,g)称为是次相容的，如果{t∈X:f(t)=g(t)}⊂{t∈X:fg(t)=gf(t)}.

注1 由定义易知，可交换映象对必是相容映象对，而相容映象对也必是次相容映象对, 但反之不真.

定义4 称函数Φ满足条件(Φ)，如果函数Φ满足条件(Φ)：Φ:[0,∞)→[0,∞)是对t不减的和右连续的，且Φ(t)0.

引理1[1]设函数Φ满足条件(Φ)，则有

(i) 对任一实数t∈[0,∞)，如果t≤Φ(t)，则t=0；

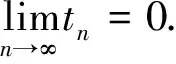
(i)mi>ni+1，ni→∞(i→∞);

(ii)d(ymi,yni)≥ε0；d(ymi-1,yni)<ε0,i=1,2,….

2 主要结果

定理1 设S,T,A,B,U和V是完备度量空间X上的6个自映象，且满足以下条件:

(i)S(X)⊂BV(X),T(X)⊂AU(X);

(ii)AU=UA,SU=US,BV=VB,TV=VT;

(iii) ∀x,y∈X,

其中Φ满足条件(Φ).如果以下条件之一被满足，则S,T,A,B,U和V有唯一的公共不动点:

1)S,AU之一连续，且(S,AU)相容,(T,BV)次相容；

2)T,BV之一连续，且(S,AU)次相容,(T,BV)相容；

3)AU,BV之一为满射，且(S,AU)和(T,BV)都次相容.

证明任取x0∈X,因S(X)⊂BV(X),T(X)⊂AU(X),故存在X中的序列{xn},{yn},使得

y2n=Sx2n=BVx2n+1,y2n+1=Tx2n+1=AUx2n+2,n=0,1,2,3,….

令dn=d(yn,yn+1)，下证

(1)

事实上，由条件(iii)可知

d(y2n-1,y2n)=d(Tx2n-1,Sx2n)=d(Sx2n,Tx2n-1)≤

(2)

若d(y2n-1,y2n-2)

下面证明{yn}是X中的Cauchy列.若不然，由引理2知，必存在某一ε0>0和正整数列{mi}，{ni}，使得

(a)mi>ni+1，ni→∞(i→∞)；

(b)d(ymi,yni)≥ε0；d(ymi-1,yni)<ε0,i=1,2,….

令ei=d(ymi,yni)，则有

ε0≤ei≤d(ymi,ymi-1)+d(ymi-1,yni)<ε0+d(ymi-1,ymi).

注意到式(1)，于上式两端让i→∞得

(3)

另一方面，因为

ei=d(ymi,yni)≤d(ymi,ymi+1)+d(ymi+1,yni+1)+d(yni+1,yni),

(4)

对式(4)右端第2项分4种情形进行讨论.

10当mi为偶，ni为奇的情形.此时由条件(iii)有

d(ymi+1,yni+1)=d(Txmi+1,Sxni+1)=d(Sxni+1,Txmi+1)≤

(5)

应用式(1)和式(3)，并注意到Φ(t)的右连续性假设，于式(5)中让i→∞取极限得

(6)

利用式(1)和式(6)，在式(4)中让i→∞取极限得ε0≤ei≤0+Φ(ε0)+0=Φ(ε0)，从而ε0≤Φ(ε0)<ε0，此为矛盾.

20当mi为偶，ni为偶的情形.此时由条件(iii)有

d(ymi+1,yni+1)=d(Txmi+1,Txni+1)≤d(Sxni,Txmi+1)+d(Sxni,Txni+1),

(7)

d(Sxni,Txmi+1)≤

(8)

应用式(1)和(3)，并注意到Φ(t)的右连续性假设，于式(8)中让i→∞取极限得

(9)

另由式(1)可得

(10)

利用式(9)和(10)，于式(7)中让i→∞取极限得

(11)

应用式(1)和(11)，于式(4)中让i→∞取极限得ε0≤ei≤0+Φ(ε0)+0=Φ(ε0)，从而ε0≤Φ(ε0)<ε0，这就得出矛盾.

同理可证mi，ni同为奇；mi为奇，ni为偶的情形也产生同样的矛盾.这些矛盾说明{yn}是X中的Cauchy列.因X完备，设yn→y*∈X，则{y2n-1}和{y2n}也都收敛于y*，即

AUx2n=y2n-1→y*,Sx2n=y2n→y*(n→∞).

(12)

1)设S,AU之一连续且(S,AU)相容，(T,BV)次相容.

如果AU连续，则{(AU)2x2n}和{(AU)Sx2n}都收敛于AUy*，又由式(12)以及(S,AU)相容得d(S(AU)x2n,(AU)Sx2n)→0(n→∞)，从而S(AU)x2n=AUy*(n→∞).由条件(iii)有

d(S(AU)x2n,Tx2n+1)≤

令n→∞得

d(AUy*,y*)≤

Φ(d(AUy*,y*)).

由此及引理1(i)可知d(AUy*,y*)=0，进而有AUy*=y*.

再由条件(ii)得

d(Sy*,Tx2n+1)≤

令n→∞，并注意到AUy*=y*可得

Φ(0)≤Φ(d(Sy*,y*))(因为Φ(t)对t不减).

由此及引理1(i)可知d(Sy*,y*)=0，进而可得Sy*=y*.

由Sy*=y*及S(X)⊂BV(X)知，∃u∈X，使y*=AUy*=Sy*=BVu.利用条件(iii)得

d(BVu,Tu)=d(Sy*,Tu)≤

Φ(0)≤Φ(d(BVu,Tu))(因为Φ(t)对t不减).

由此及引理1(i)可知d(BVu,Tu)=0，进而可得BVu=Tu.因(T,BV)次相容，故Ty*=T(BV)u=(BV)Tu=BVy*.

下证Ty*=y*.事实上，由条件(iii)可得

d(y*,Ty*)=d(Sy*,Ty*)≤

Φ(d(y*,Ty*)).

从而由引理1(i)可知d(y*,Ty*)=0，即Ty*=y*.于是y*=BVy*=Ty*=Sy*=AUy*，即y*是S,T,AU,BV的公共不动点.

如果S连续，则{S2x2n}和{S(AU)x2n}都收敛于Sy*，由式(12)以及(S,AU)的相容性得d(S(AU)x2n,(AU)Sx2n)→0(n→∞)，从而 (AU)Sx2n→Sy*(n→∞).由条件(iii)有

d(S2x2n,Tx2n+1)≤

令n→∞得

由此及引理1(i)可知，有d(Sy*,y*)=0，进而可得Sy*=y*.由于y*=Sy*∈S(X)⊂BV(X)，故∃v∈X，使y*=Sy*=BVv.再由条件(iii)可得

d(S2x2n,Tv)≤

令n→∞，并注意到Sy*=BVv得

d(Sy*,Tv)≤

Φ(0)≤Φ(d(Sy*,Tv)).

由此及引理1(i)可知，有d(Sy*,Tv)=0，进而可得Sy*=Tv，于是y*=Sy*=BVv=Tv.考虑到(T,BV)的次相容性，有Ty*=T(BV)v=(BV)Tv=BVy*.再次利用条件(iii)，有

d(Sx2n,Ty*)≤

令n→∞，并注意到BVy*=Ty*得

d(y*,Ty*)≤

Φ(d(y*,Ty*)).

由此及引理1(i)可知d(y*,Ty*)=0，进而可得y*=Ty*.由于y*=Ty*∈T(X)⊂AU(X)，故∃w∈X，使y*=Ty*=AUw.利用条件(iii)，并注意到BVy*=Ty*=AUw可得

d(Sw,y*)=d(Sw,Ty*)≤

Φ(0)≤Φ(d(Sw,y*)),

由此及引理1(i)可知d(Sw,y*)=0，进而可得y*=Sw，于是y*=AUw=Sw.又由(S,AU)的相容性易得Sy*=S(AU)w=(AU)Sw=AUy*，因此就有y*=Sy*=AUy*=Ty*=BVy*.

下面证明Uy*=y*，Ay*=y*.事实上，利用条件(iii)得

d(SUy*,Tx2n+1)≤

因为US=SU，AU=UA，所以USy*=SUy*=Uy*，(AU)Uy*=U(AU)y*=Uy*.于上式中令n→∞，并注意到AUy*=y*可得

d(Uy*,y*)≤

Φ(d(Uy*,y*)).

从而由引理1(i)可知，d(Uy*,y*)=0，即Uy*=y*.进而由AUy*=y*可得Ay*=y*.

下面证明Vy*=y*，By*=y*.事实上，利用条件(iii)得

d(Sx2n,TVy*)≤

因为BV=VB,TV=VT，BVy*=y*，所以TVy*=VTy*=Vy*，(BV)Vy*=V(BV)y*=Vy*.于上式中令n→∞，并注意到Ty*=y*，BVy*=Ty*以及Φ(t)的不减性可得

d(y*,Vy*)≤

Φ(d(y*,Vy*)).

从而由引理1(i)可知，d(y*,Vy*)=0，即Vy*=y*.进而由BVy*=y*可得By*=y*.

综上，有y*=Sy*=Ty*=Ay*=By*=Uy*=Vy*，即y*是S,T,A,B,U和V的公共不动点.

下证公共不动点的唯一性.设z也是S,T,A,B,U和V的一个公共不动点，则由条件(iii)有

d(y*,z)=d(Sy*,Tz)≤

Φ(d(y*,z)).

由此及引理1(i)可知d(y*,z)=0，即y*=z，因此y*是S,T,A,B,U和V的唯一公共不动点.

2) 当T,BV之一连续，且(S,AU)次相容,(T,BV) 相容时，类似1)可证.

3) 设AU,BV之一为满射，且(S,AU)和(T,BV)都次相容.

如果AU是满射，则对y*∈X,∃u∈X,使AUu=y*.由条件(iii)得

d(Su,Tx2n+1)≤

(13)

令n→∞得d2(Su,y*)≤Φ(0)≤Φ(d(Su,y*))，由此及引理1(i)可知，d(Su,y*)=0，即Su=y*，因而Su=AUu=y*.又(S,AU)是次相容的，故有AUy*=(AU)Su=S(AU)u=Sy*.以y*代替式(13)中的u可得Sy*=y*，于是AUy*=Sy*=y*.类似1)可证y*是S,T,A,B,U和V的唯一公共不动点.

当B是满射时同理可证y*是S,T,A,B,U和V的唯一公共不动点.至此定理1获证.

注2 即使在定理1中分别取①S=T；②A=B；③U=V；④S=T,A=B且U=V；⑤S=T且A=B=I(I表恒等映象)；⑥S=T,A=B且U=V=I这几种特殊情况，所对应的结果也是全新的.

推论1 设(X,d)是完备度量空间，{Ti}i∈I(I是指标集，I的势不小于2)是X上的自映象族，A,B,U,V是X上的自映象，若{Ti}i∈I，A,B,U,V满足以下条件：

(i)Ti(X)⊂BV(X)，Ti(X)⊂AU(X)(∀i∈I)；

(ii)TiV=VTi,AU=UA,BV=VB；

(iii) ∀x,y∈X，i,j∈I(i≠j) ，有

其中函数Φ满足条件(Φ).如果以下条件之一被满足，则A,B,{Ti}i∈I在X中有唯一的公共不动点:

1)Ti(∀i∈I),A之一连续且(Ti,AU)相容，(Ti,BV)次相容；

2)Ti(∀i∈I),B之一连续且(Ti,AU)次相容，(Ti,BV)相容；

3)A,B之一为满射且(Ti,AU)和(Ti,BV)(∀i∈I)都次相容.

证明对任意的i,j,m∈I，i≠j,i≠m，由定理1知A,B,U,V,Ti,Tj存在唯一的公共不动点xij，A,B,U,V,Ti,Tm存在唯一的公共不动点xim，但由条件(iii)可得

d(xij,xim)=d(Tixij,Tmxim)≤

Φ(d(xij,xim)),

因此由引理1(i)可知d(xij,xim)=0，进而xij=xim.由i,j,m的任意性即得A,B,U,V,{Ti}i∈I在X中存在唯一的公共不动点.

定理2 设(X,d)是完备度量空间，A,B,U,V,{Ti}i∈I(I是指标集，势不小于2)分别是X上的自映象和自映象族，且满足∀i∈I，有Ti(X)⊂BV(X),Ti(X)⊂AU(X)，(Ti,AU)和(Ti,BV)均是可交换映象.若存在正整数n，使得A,B,U,V,{Ti}i∈I满足以下条件：

(i)A,B,U,V,{Ti}i∈I之一连续；

(ii) ∀x,y∈X，i,j∈I,i≠j，有

其中函数Φ满足条件(Φ),则A,B,U,V,{Ti}i∈I在X中存在唯一的公共不动点.

Φ(d(Tiz,z)).

由引理1(i)可知d(Tiz,z)=0，进而Tiz=z.故z是A,B,U,V,{Ti}i∈I的公共不动点，其唯一性由条件(iii)易证.证毕.

注3 本文结果也是文献[11-12]中相应结果的进一步改进和发展.

[1] 张石生.不动点理论及其应用[M].重庆：重庆出版社，1984.

[2] 谷峰.关于Φ扩张相容映象的公共不动点定理[J].宝鸡文理学院学报：自然科学版，2001，21(3)：176-179.

[3] Li Yaqiong, Gu Feng.Common fixed point theorem of Altman integral type mappings[J].J Nonlinear Sci Appl,2009,2(4):214-218.

[4] 李付成,谷峰.对称空间中的重合点和公共不动点定理[J].杭州师范大学学报:自然科学版，2010，9(2)：102-106.

[5] 张军贺,陆竞,谷峰.涉及到四个映象的一个新的公共不动点定理[J].杭州师范大学学报:自然科学版，2010,9(6)：413-417.

[6] 李亚琼，谷峰.关于(Ag)型φ-弱交换映象的公共不动点[J].西南大学学报:自然科学版，2009,31(8):138-140.

[7] 李亚琼，谷峰.两对相容映象的一个新的公共不动点定理[J].杭州师范大学学报:自然科学版，2009,8(4):257-260.

[8] 陈军民,谷峰.满足积分型压缩条件的一个公共不动点定理[J].杭州师范大学学报:自然科学版，2008，7(5)：338-344.

[9] Jungck G.Compatible mappings and common fixed points[J].Internat J Math﹠Math Sci，1986，9(4)：771-779.

[10] 刘立山.(次)相容映象的公共不动点定理与广义Ishikawa迭代逼近定理[J].曲阜师范大学学报：自然科学版，1990，16(2)：40-44.

[11] 李凤友,刘斌.关于几类压缩映象的不动点定理[J].天津师范大学学报：自然科学版，1996，16(1):1-7.

[12] 巨小维,谷峰.一类Φ-压缩映象的公共不动点定理[J].商丘师范学院学报,2007,23(6):21-25.

TheCommonFixedPointTheoremsofSixMappingswithΦ-ContractionConditions

LU Jing

(College of Science, Hangzhou Normal University, Hangzhou 310036, China)

Using the compatible and subcompatible conditions of self-mapping pair in metric spaces, the paper discussed the existence and uniqueness of common fixed point for a class ofΦ-contractive mappings in complete metric spaces, and obtained some new common fixed theorem.

compatible mapping pair; subcompatible mapping pair;Φ-contractive type mapping; common fixed point

2011-01-11

陆 竞(1958—)，男，浙江杭州人，副教授，主要从事函数理论研究.E-mail: wllujing@sina.com

10.3969/j.issn.1674-232X.2011.04.002

O177MSC2010: 47H10；54H25；58C30

A

1674-232X(2011)04-0298-07