直觉模糊BCK-代数
2011-11-23彭家寅
彭家寅
(1.四川省高等学校 数值仿真重点实验室, 四川 内江 641112;2.内江师范学院 数学与信息科学学院, 四川 内江 641112)
直觉模糊BCK-代数
彭家寅1,2
(1.四川省高等学校 数值仿真重点实验室, 四川 内江 641112;2.内江师范学院 数学与信息科学学院, 四川 内江 641112)
系统研究了作为Zadeh模糊理论重要扩展的Atanassov直觉模糊BCK-代数. 首先,引入直觉模糊BCK-代数和它的水平代数的概念,讨论了它们相关性质.其次,研究了直觉模糊BCK-代数的同态与同构像和逆像的性质,获得了直觉模糊BCK-代数的同态像和逆像仍为直觉模糊BCK-代数.最后,给出了直觉模糊集上的直觉模糊关系、强直觉模糊关系的概念,对直觉模糊集的笛卡儿积进行了定义,揭示了直觉模糊BCK-代数与其积代数间的若干关系.
直觉模糊集; 直觉模糊BCK-代数; 水平代数; 直觉模糊关系; 笛卡儿积
0 引言
1986年保加利亚学者K.Atanassov[1]提出了直觉模糊集的概念,推广并发展了L.A. Zadeh提出的模糊集概念.这种模糊集被提出之后,引起许多学者的浓厚兴趣,人们针对这一基本理论,做了大量有意义的工作.文[2]给出了直觉模糊集的扩张原理,并讨论了直觉模糊集的并、交等扩张运算;文[3]引入了直觉模糊集的<λ1,λ2>-截集的概念,建立了一系列分解定理、表现定理与扩张原理;K.Atanassov和G.Gargov[4]提出了直觉模糊逻辑的理论框架;H.Bustince和P.Burillo[5]提出直觉模糊关系和模糊鞅的理论;D.Coker[6]引入了直觉模糊拓扑空间的定义;文[7-9]则侧重于代数方面研究,引入了直觉模糊群、直觉模糊环和直觉模糊域等概念,并在同态与同构意义下,研究了它们的像和原像的结构特征问题.1966年Y.Imai和K.Iseki[10]提出了BCK-代数的概念,O.G.Xi[11]应用了L.A. Zadeh提出的模糊集概念研究了模糊BCK-代数.本文在考察Atanassov直觉模糊集与Zadeh模糊集之间关系的基础上,引入直觉模糊BCK-代数和它的水平代数的概念,研究它们的相关关系和运算性质,讨论了在同态与同构意义下,直觉模糊BCK-代数的像和逆像的性质,给出了直觉模糊集的笛卡儿积概念,并把它归结到直觉模糊关系上来刻画直觉模糊BCK-代数与其积代数间性质.
1 预备知识
定义1.1[1]设X是一个非空经典集合,称形如
A={
的三重组为X上的一个直觉模糊集,其中μA:X→[0,1]和νA:X→[0,1]均为X上的普通模糊集,这里μA(x)和νA(x)分别表示X上元素x属于A的隶属度和非隶属度.
为了方便,以下我们将直觉模糊集A满足的条件“0≤μA(x)+νA(x)≤1”省略,并简记为A={
定义1.2[1]设X是一个非空经典集合,A,B∈IFS[X]且具有形式
A={
规定序及运算如下:
1)A⊆B当且仅当μA(x)≤μB(x)且νA(x)≥νB(x),∀x∈X;
2)A=B当且仅当μA(x)=μB(x)且νA(x)=νB(x),∀x∈X;
3)Ac={
4)A∩B={
5)A∪B={
6)A={
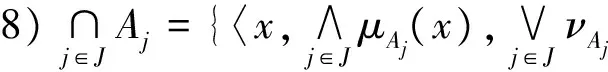
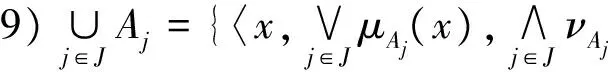
其中Aj={
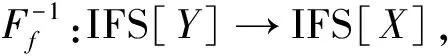
Ff(A){〈y,Ff(μA)(y),(νA)(y)〉|y∈Y},
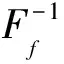
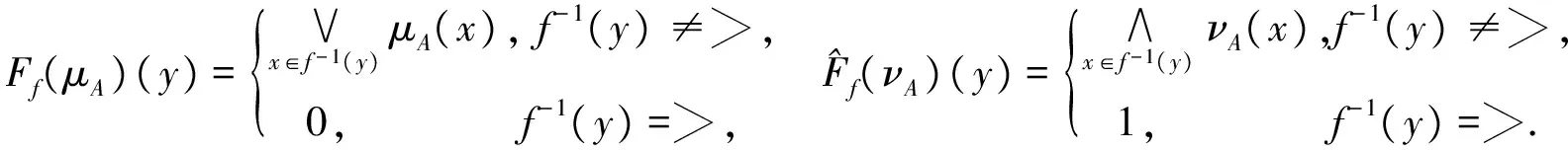
定义1.4[3]设A∈IFS[X],λ1,λ2∈[0,1]且λ1+λ2≤1,称集合
A〈λ1,λ2〉={x∈X|μA(x)≥λ1,νA(x)≤λ2},A〈λ1,λ2〉·={x∈X|μA(x)>λ1,νA(x)<λ2},
A〈λ1·,λ2〉={x∈X|μA(x)>λ1,νA(x)≤λ2},A〈λ1,λ2·〉={x∈X|μA(x)≥λ1,νA(x)<λ2}
分别为A的〈λ1,λ2〉-截集、〈λ1,λ2〉·-截集、〈λ1·,λ2〉-截集和〈λ1,λ2·〉-截集.
定义1.5[10]称一个(2,0)型代数(X;*,0)为BCK-代数,如果对任意x,y,z∈X,有
(i) ((x*y)*(x*z))*(z*y)=0,
(ii) (x*(x*y))*y=0,
(iii)x*x=0,
(iv) 0*x=0,
(v)x*y=y*x=0⟹x=y.
在任何一个BCK-代数X中,下列性质成立:
1) (x*y)*z=(x*z)*y,
2)x*0=x.
BCK-代数X的一个非空子集S叫做X的一个子代数,如果任意x,y∈S,都有x*y∈S.
2 直觉模糊BCK-代数
定义2.1 设A={
定理2.1 设A为BCK-代数X的任一直觉模糊代数,则对任意x∈X,有μA(0)≥μA(x)且νA(0)≤νA(x).
证明因为X为一个BCK-代数,所以对任意x∈X有x*x=0,于是
μA(0)=μA(x*x)≥μA(x)∧μA(x)=μA(x),
νA(0)=νA(x*x)≤νA(x)∨νA(x)=νA(x).
定理2.2 设A为BCK-代数X的任一直觉模糊集合,A为X的直觉模糊代数的充分必要条件是对任意λ1,λ2∈[0,1],A〈λ1,λ2〉为X的子代数或空集.
证明必要性: 设x,y∈A〈λ1,λ2〉,则μA(x)≥λ1,μA(y)≥λ1,νA(x)≤λ2,νA(y)≤λ2.因A为X的直觉模糊代数,所以μA(x*y)≥μA(x)∧μA(y)≥λ1且νA(x*y)≤νA(x)∨νA(y)≤λ2,于是x*y∈A〈λ1,λ2〉,故A〈λ1,λ2〉为X的子代数.
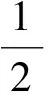
1) 当μA(x0*y0)<λ1,μA(x0)>λ1且μA(y0)>λ1时,令λ=νA(x0)∨νA(y0),则νA(x0)≤λ且νA(x0)≤λ.因A为直觉模糊集,则λ1+λ≤μA(x0)+νA(x0)≤1或λ1+λ≤μA(y0)+νA(y0)≤1.于是x0,y0∈A〈λ1,λ〉,但x0*y0∉A〈λ1,λ〉,这与A〈λ1,λ〉为X的子代数矛盾.
2) 当νA(x0*y0)>λ2,νA(x0)<λ2且νA(y0)<λ2时,令λ=μA(x0)∧μA(y0)∧(1-λ2),则μA(x0)≥λ,μA(y0)≥λ且λ+λ2≤1.从而x0,y0∈A〈λ,λ2〉,但x0*y0∉A〈λ,λ2〉,
这与A〈λ,λ2〉为X的子代数矛盾.这样就证明了充分性.
定理2.3 设A为BCK-代数X的任一直觉模糊代数,则对任意x∈X,有
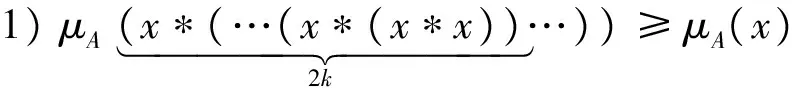
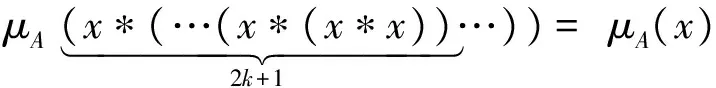

证明因为x*0=x,则对任意x∈X有
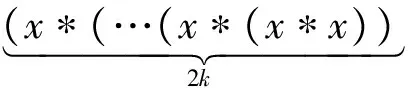
同理可证明余下部分.
命题2.4 设A为BCK-代数X的任一直觉模糊代数,x1,x2,…,xn是X的任意n个元.如果在集合{x1,x2,…,xn}中至少有一个元xk等于x1,则对任意x∈X有
μA((…((x1*x2)*x3)…)*xn)≥μA(x),νA((…((x1*x2)*x3)…)*xn)≤νA(x).
证明对任意x,y,z∈X,有(x*y)*z=(x*z)*y,因此我们总可把xk交换到x2的位置上.应用x1*x1=0,0*xi=xi有
同理证明第二个关系式.
定义2.2 设A为BCK-代数X的任一直觉模糊代数,子代数A〈λ1,λ2〉,λ1,λ2∈[0,1],叫做A的水平代数.
定理2.5 BCK-代数X的任何子代数都可作为X的某些直觉模糊代数的一个水平代数.
证明设S是BCK-代数X的任何一个子代数,定义X上的三重组集A={〈x,μA(x),νA(x)〉|x∈X}如下:
其中t和t′是(0,0.5)中的两个固定的数且t+t′<1.显然,0≤μA(x)+νA(x)≤1,因此A是X上的直觉模糊集且A〈t,t′〉=S.我们可以断定A是X上的一个直觉模糊代数.事实上,对任意x,y∈X,若x,y∈S,则x*y∈S,于是μA(x*y)=t=μA(x)∧μA(y),νA(x*y)=t′=νA(x)∨νA(y).若x∉S或y∉S,则μA(x)∧μA(y)=0≤μA(x*y),νA(x*y)≤1=νA(x)∨νA(y).总之,对任意x,y∈X,有μA(x*y)≥μA(x)∧μA(y)且νA(x*y)≤νA(x)∨νA(y).
定理2.6 设A为BCK-代数X的任一直觉模糊代数,则A的两个水平代数A〈λ1,λ2〉,A〈t1,t2〉(λ1 证明对于λ1 注: 如果X是有限BCK-代数,则X的子代数的个数也是有限的,而BCK-代数X的直觉模糊代数A的水平代数形式上是无限的.因为水平代数也是X的子代数,所以BCK-代数X的直觉模糊代数A的所有水平代数并不是互不相同的.作为定理2.6的结果,有限BCK-代数X的直觉模糊代数A的水平代数形成一个链.因为μA(0)≥μA(x)且νA(0)≤νA(x),记λ0=μA(0),t0=νA(0),所以有如下链: A〈λ0,t0〉⊂A〈λ1,t1〉⊂…⊂A〈λm,tn〉=X, 这里λ0>λ1>…>λm,t0 定理2.7 设A和B均为BCK-代数X的直觉模糊代数, 则A∩B是BCK-代数X的直觉模糊代数. 证明设A={ μA∩B(x*y)=μA(x*y)∧μB(x*y)≥(μA(x)∧μA(y))∧(μB(x)∧μB(y))= (μA(x)∧μB(x))∧(μA(y)∧μB(y))=μA∩B(x)∧μA∩B(y). 同理νA∩B(x*y)≤νA∩B(x)∨νA∩B(y).故A∩B是BCK-代数X的直觉模糊代数. 定理2.9 设A为BCK-代数X的直觉模糊代数,则A是BCK-代数X的直觉模糊代数. 证明设A={ 定理2.10 设A为BCK-代数X的直觉模糊代数,则A是BCK-代数X的直觉模糊代数. 证明设A={ 注 按直觉模糊代数定义容易知道,对BCK-代数X的任意两个直觉模糊代数A和B,不能推出Ac和A∪B是BCK-代数X的直觉模糊代数. 定理3.1 设X,Y均为BCK-代数,f:X→Y是同态映射.若A是BCK-代数X的直觉模糊代数,则Ff(A)是BCK-代数Y的直觉模糊代数. 情况(ii) 若f-1(y1)≠⟩且f-1(y2)≠⟩,若 Ff(μA)(y1*y2) (1) 或 (2) 推论3.3 设X,Y均为BCK-代数,f:X→Y是同态映射.则下列结论成立: 证明由推论1、定理1和定理2易证. 推论3.4 设X,Y均为BCK-代数,f:X→Y是同态映射.则下列结论成立: 1) 若A为BCK-代数X的直觉模糊代数,则Ff(A)和Ff(A)均为BCK-代数Y的直觉模糊代数; 证明由定理2.9、定理2.10、定理3.1和定理3.2易证. 证明 任意x∈X,令f(x)=y,因f是同构映射,所以f-1(y)={x},于是 定义4.1[12]设X和Y为非空经典集合.定义在直积空间X×Y上的直觉模糊集称为从X到Y之间的二元直觉模糊关系.记为 R={〈(x,y),μR(x,y),νR(x,y)〉|x∈X,y∈Y}, 其中μR:X×Y→[0,1]和νR:X×Y→[0,1]满足条件0≤μR(x,y)+νR(x,y)〉≤1对任意(x,y)∈X×Y都成立. 若X=Y,则称从X到Y之间的二元直觉模糊关系R为X上的直觉模糊关系. 定义4.2 设R={〈(x,y),μR(x,y),νR(x,y)〉|x,y∈X}是X上的直觉模糊关系,A={ 引理4.1 设A={ A×B={〈(x,y),μA×B(x,y),νA×B(x,y)〉|x,y∈X}, 其中μA×B(x,y)=μA(x)∧μB(y),νA×B(x,y)=νA(x)∨νB(y).则A×B为X上的直觉模糊关系. 定理4.2 设A={ 证明对任意(x,y)∈X×X,有μA(x*y)≥μA(x)∧μA(y),νA(x*y)≤νA(x)∨νA(y),μB(x*y)≥μB(x)∧μB(y)和νB(x*y)≤νB(x)∨νB(y).于是对任意(x,y),(x′,y′)∈X×X,有 μA×B((x,y)*(x′,y′))=μA×B(x*x′,y*y′)=μA(x*x′)∧μB(y*y′)≥ (μA(x)∧μA(x′))∧(μB(y)∧μB(y′))≥(μA(x)∧μB(y))∧(μA(x′)∧μB(y′))= μA×B(x,y)∧μA×B(x′,y′). 类似可证,νA×B((x,y)*(x′,y′))≤νA×B(x,y)∨νA×B(x′,y′).故A×B为BCK-代数X×X上的直觉模糊代数. 定理4.3 设A={ 1)∀x∈X,有μA(0)≥μA(x)或μB(0)≥μB(x); 2)∀x∈X,有νA(0)≤νA(x)或νB(0)≤νB(x); 3)∀x∈X,有μB(0)≥μA(x)或μB(0)≥μB(x); 4)∀x∈X,有νB(0)≤νA(x)或νB(0)≤νB(x); 5)∀x∈X,有μA(0)≥μA(x)或μA(0)≥μB(x); 6)∀x∈X,有νA(0)≤νA(x)或νA(0)≤νB(x); 7) 若任意x∈X,μA(0)≥μB(x)且νA(0)≤νB(x),则B是BCK-代数X上的直觉模糊代数; 8) 若任意x∈X,μB(0)≥μA(x)且νB(0)≤νA(x),则A是BCK-代数X上的直觉模糊代数. 证明1) 若存在x,y∈X,使得μA(0)<μA(x)且μB(0)<μB(y),于是μA×B(x,y)=μA(x)∧μB(y)>μA(0)∧μB(0)=μA×B(0,0).由定理2.1知,这与A×B为直觉模糊代数相矛盾. 3) 若存在x,y∈X使得μB(0)<μA(x)且μB(0)<μB(y),则μA×B(x,y)=μA(x)∧μB(y)>μB(0)∧μB(0)=μB(0)≥μA(0)∧μB(0)=μA×B(0,0),由定理2.1知,这与A×B为直觉模糊代数相矛盾. 4) 若存在x,y∈X使得νB(0)>νA(x)且νB(0)>νB(y),则νA×B(x,y)=νA(x)∨ νB(y)<νB(0)∨νB(0)=νB(0)≤νA(0)∨νB(0)=νA×B(0,0),由定理2.1知,这与A×B为直觉模糊代数相矛盾. 2) 5) 6)的证明分别类似1) 3) 4). 7) 对任意x∈X,μA(0)≥μB(x),由于A×B为直觉模糊代数,所以μA×B((x,y)*(x′,y′))≥μA×B(x,y)∧μA×B(x′,y′),即μA×B(x*x′,y*y′)≥μA×B(x,y)∧μA×B(x′,y′),所以μA(x*x′)∧μB(y*y′)≥μA(x)∧μB(y)∧μA(x′)∧μB(y′).令x=x′=0,于是μA(0)∧μB(y*y′)≥μA(0)∧μB(y)∧μA(0)∧μB(y′),即μB(y*y′)≥μB(y)∧μB(y′). 又任意x∈X有νA(0)≤νB(x),注意到A×B为直觉模糊代数有 νA×B((x,y)*(x′,y′))≤νA×B(x,y)∨νA×B(x′,y′), 即νA×B(x*x′,y*y′)≤νA×B(x,y)∨νA×B(x′,y′),所以νA(x*x′)∨νB(y*y′)≤νA(x)∨νB(y)∨νA(x′)∨νB(y′).令x=x′=0,则νA(0)∨νB(y*y′)≤νA(0)∨νB(y)∨νA(0)∨νB(y′),即νB(y*y′)≤νB(y)∨νB(y′). 综上所述,B是BCK-代数X上的直觉模糊代数. 8) 类似于7)的证明可以得到结果. 定义4.3 设R={〈(x,y),μR(x,y),νR(x,y)〉|x,y∈X}是X上的直觉模糊关系,A={ 定理4.4 设A={ 证明必要性:对任意(x,y),(x′,y′)∈X×X,因A为直觉模糊代数,所以 μR((x,y)*(x′,y′))=μR(x*x′,y*y′)=μA(x*x′)∧μA(y*y′)≥ μA(x)∧μA(x′)∧μA(y)∧μA(y′)= (μA(x)∧μA(y))∧(μA(x′)∧μA(y′))=μR(x,y)∧μR(x′,y′). 类似地有νR((x,y)*(x′,y′))≤νR(x,y)∨νR(x′,y′),故R为BCK-代数X×X上的直觉模糊代数. 充分性: 因R为直觉模糊代数,对任意(x,y),(x′,y′)∈X×X,有 μR((x,y)*(x′,y′))≥μR(x,y)∧μR(x′,y′), 即 μA(x*x′)∧μA(y*y′)≥μA(x)∧μA(x′)∧μA(y)∧μA(y′). 令y=x且x′=y′,则μA(x*x′)≥μA(x)∧μA(x′).同理可以证明,νA(x*x′)≤νA(x)∨νA(x′).故A为BCK-代数X上的直觉模糊代数. [1] Atanassov K. Intuitionistic fuzzy sets?[J]. Fuzzy Sets and Systems, 1986,20(1):87-96. [2] 李晓萍,王贵君. 直觉模糊集的扩张运算?[J]. 模糊系统与数学, 2002,16(1):40-46. [3] 刘华文. 直觉Fuzzy集的基本定理?[J]. 工科数学, 2000,16(1):55-60. [4] Atanassov K, Gargov G. Elements of intuitionistic fuzzy logic?[J]. Fuzzy Sets and Systems, 1998, 95(1):39-52. [5] Bustince H, Burillo P. Structures on intuitionistc fuzzy relations?[J]. Fuzzy Sets and Systems, 1996, 78(3):293-303. [6] Dogan Coker. An introduction to intuitionistic fuzzy topllogic spaces?[J]. Fuzzy Sets and Systems, 1997, 88(1):81-89. [7] 李晓萍,王贵君. 直觉模糊群与它的同态像?[J]. 模糊系统与数学, 2000,14(1):45-50. [8] 姚炳学,谷文祥. 环的生成模糊理想?[J]. 东北师范大学, 2002,34(4):8-14. [9] 孙绍权,谷文祥. Fuzzy商代数与同态基本定理?[J].东北师范大学, 2002,34(2):22-25. [10] Imai Y, Iseki K. On axiom systems of propositional calculi XIV?[J]. Proc Japan Acadwmy, 1966, 41: 19-22. [11] Xi O G. Fuzzy BCK-algebras?[J]. Math Japon, 1991,36:935-942. [12] 雷英杰,王宝树,苗启广. 直觉模糊关系及其合成运算?[J]. 系统工程理论与实践, 2005(2):113-133. [责任编辑:李春红] IntuitionisiticFuzzyBCK-algebras PENG Jia-yin (1.Key Laboratory of Numerical Simulation of Sichuan Provice, Neijiang Sichuan 641112, China) (2.School of Mathematics and Information Science, Neijiang Normal University, Neijiang Sichuan 641112, China) The problems of intuitionistic fuzzy BCK-algebras on intuitionisitic fuzzy sets by Atanassov, which is a significant extension of fuzzy set theory by Zadeh, are systemically investigated. At first, the notions of intuitionistic fuzzy BCK-algebras and its level algebras are introduced, and their properties are discussed. The next, some properties of the homomorphic (isomorphic) image and inverse image of intuitionistic fuzzy BCK-algebras are studied, it is obtained that the homomorphic (isomorphic) image and inverse image of intuitionistic fuzzy BCK-algebras are still intuitionistic fuzzy BCK-algebras. Lastly, the notions of intuitionistic fuzzy relation, strongest intuitionistic fuzzy relation and Cartesian product of intuitionisitic fuzzy sets are given, some relations between intuitionistic fuzzy BCK-algebras and its product algebras are exposed. intuitionisitic fuzzy set; intuitionistic fuzzy BCK-algebra; level algebra; intuitionistic fuzzy relation; Cartesian product O159 A 1671-6876(2011)04-0296-08 2010-12-05 四川省科技厅重点资助项目(2006J13-035); 四川省教育厅重点实验室专项资助项目(2006ZD050) 彭家寅(1962-), 男, 四川资中人, 教授, 主要从事模糊数学与人工智能方面的研究.
3 直觉模糊BCK-代数的同态和同构像与原像

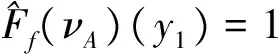
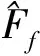
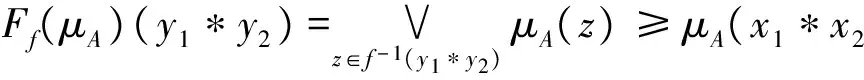

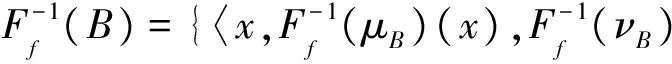
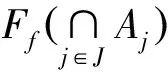



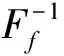
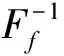

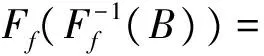
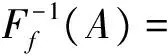
4 直觉模糊BCK-代数的笛卡儿积
