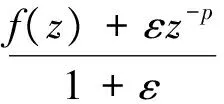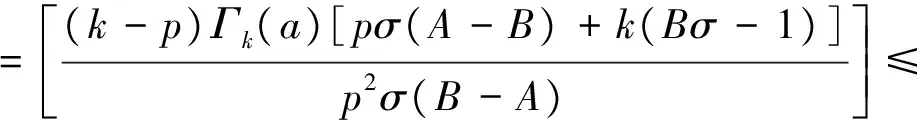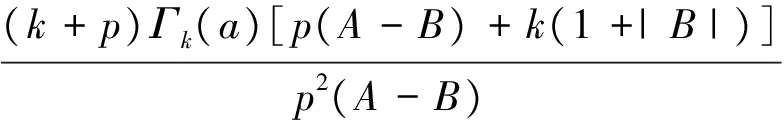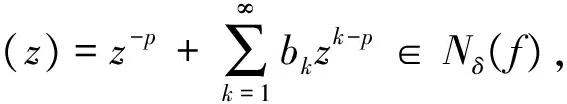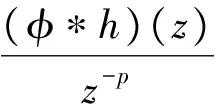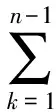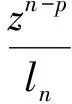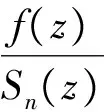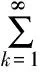亚纯多叶函数某一子类的局部和

2011-11-23周伟

淮阴师范学院学报（自然科学版） 2011年4期

关键词：亚纯子类淮安

周伟

(淮阴师范学院数学科学学院, 江苏淮安 223300)

亚纯多叶函数某一子类的局部和

周伟

(淮阴师范学院数学科学学院, 江苏淮安 223300)

亚纯多叶函数; 邻域; 局部和

0 引言

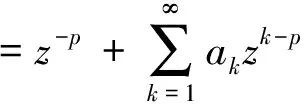
定义1 设∑P表示形如

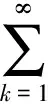
(1)

且在E={z:0<|z|<1}内解析的p-叶函数的全体组成的函数类.

定义2 设f∈∑p,定义关于∑p的线性算子Lp(a,c)如下:

Lp(a,c)f(z)=φp(a,c;z)*f(z)

(2)

易证线性算子Lp(a,c)满足:

由线性算子Lp(a,c)定义如下一个函数类:

定义3 若f∈∑p且满足

(3)

其中

z∈E;-1≤B

则称f(z)属于类Ωp(a,c;A,B).

定义4 设f∈∑p且形如(1)式,定义f的δ邻域为

(4)

1 主要结论

以下假定a>0且c>0.

定理1 设f∈Ωp(a,c;A,B),且f形如(1)式.若f满足

则Nδ(f)⊂Ωp(a,c;A,B).

证明由(3)式可得g∈Ωp(a,c;A,B)当且仅当

(z∈E;σ∈C;|σ|=1),

等价于

(5)

其中

(6)

由(6)式可得:

而且在定理的假设下,由(5)式可得:

令

则

从而,对于σ∈C且满足|σ|=1,有

故可得φ∈Ωp(a,c;A,B).定理得证.

定理2 设f∈∑p且形如(1)式,定义局部和为

(7)

则

(8)

且

(9)

(8)和(9)式的界都是精确的.

证明(i)易得:z-p∈Ωp(a,c;A,B).由定理1和(7)式可得:N1(z-p)⊂Ωp(a,c;A,B),从而可得:f∈Ωp(a,c;A,B).

(ii)在定理2中(ii)的假设下,由(7)式可得:

lk+1>lk>1 (k∈N).

从而

(10)

令

利用(10)式可得:

从而可得(8)式成立.

若取

(11)

则

从而可得(8)式中界的精确性.

类似地,若令

由(10)式可得:

从而可得(9)式成立.

由(11)式给出的f(z)也是(9)式的极值函数,定理得证.

[1] Srivastava H M, Liu J L. Subclasses of meromorphically multivalent functions associated with a certain linear operator?[J].Math Comput Modelling, 2004, 39(1):35-44.

[2] Srivastava H M,Patel J. Some subclasses of multivalent functions involving a certain linear operator?[J].J Math Anal Appl, 2005, 310(1):209-228.

[3] Goel R M,Sohi N S. A new criteron for p-valent functions?[J]. Proc Amer Math Soc, 1980, 78(3):353-357.

[4] Liu J L. A linear operator and its applications on meromorphic p-valent functions?[J].Bull Inst Math Acad Sini, 2003,31(1):23-32.

[5] Zhou C H. A family of meromorphic multivalent functions defined by a linear operator?[J].Journal of Shandong University of Technology, 2006, 20(3):13-15.

[责任编辑：李春红]

ASubclassofMeromorphicMultivalentFunctionsofLocalSums

ZHOU Wei

(College of Mathematics, Huaiyin Normal University, Huaian Jiangsu 223300, China)