用SGC053超导重力仪观测资料对gPh058重力仪格值的精密测定*

张 锐 韦 进 刘子维 李 辉 郝洪涛

(1)地壳运动监测工程研究中心，北京 100036 2)中国地震局地震研究所，武汉 430071 3)武汉大学测绘学院，武汉430079)

用SGC053超导重力仪观测资料对gPh058重力仪格值的精密测定*

张 锐1)韦 进2，3)刘子维2，3)李 辉2)郝洪涛2)

(1)地壳运动监测工程研究中心，北京 100036 2)中国地震局地震研究所，武汉 430071 3)武汉大学测绘学院，武汉430079)

利用中国地震局武汉引力与固体潮观测站SGC053超导重力仪与gPh058重力仪的同址观测资料，采用切比雪夫多项式模型，利用同址比测方法对gPh058重力仪格值系数进行精密测定。对同址比测方法中的多项式阶数、采样数、采样时段3个可能影响格值系数的因素分析结果表明，重力仪的稳定情况是采样时段3个因素中影响最大的。计算不同采样时段的格值系数，取其加权均值作为gPh058的格值系数为：1.008 4±0.00 09×10-8ms-2/mV。格值系数的测定前后同址观测数据的分析表明：测定后gPh058重力仪可获得与超导重力仪相近的潮汐参数。经SGC053同址观测数据的漂移改正，残差周日波和半日波振幅只有测定前的1/4，而残差变幅只有±7× 10-8ms-2。虽然gPh058重力仪出厂前进行过标定，然而同址观测测定所获得的格值系数更加可靠。

SGC053超导重力仪;gPhone058重力仪;格值系数;同址观测;潮汐参数

1 引言

gPhone重力仪是由美国Micro-g LaCoste公司生产的金属弹簧相对重力仪，具有高精度、低漂移、高采样率、测程大等特点，同时为了实现地震重力组网观测，对仪器进行了网络化改造［1］。重力仪格值系数的偏离和潮汐基准的不统一，将对重力仪组网观测资料的解释和应用带来了困难［2］，因此如何获得gPhone重力仪高精度的格值系数，并将仪器观测数据统一到同一个潮汐基准上是一个十分重要的基础性研究。2001年Francis利用SGC021超导重力仪在比利时利用3个月的同址观测资料对LCR906号重力仪进行标定得到格值系数的相对精度1‰［4］。2003年陈晓东［5］利用GWR032超导重力仪观测资料精密测定了LCRET20重力仪格的值。可以看出通过同址比测法可以获得较好的标定精度。

2009—2010年，将引进的gPhone重力仪和中国地震局武汉引力与固体潮观测站SGC053超导重力仪进行了同址测试，其中gPhone058重力仪(简称gPh058)和SGC053进行了为期244天同址观测。本文利用切比雪夫多项式模型对gPhone重力仪进行精密测定。

2 精密测定重力仪格值系数模型

结合国内外科学家对重力仪的研究［4-6，10］，并考虑弹簧型重力仪的漂移复杂性［10］，本文利用切比雪夫多项式模型来精密测定格值系数。其模型为

gsg为超导重力仪观测的重力值;ggph为gPh058重力仪观测的数据，A为格值系数，Ci为切比雪夫多项式系数，Ti为切比雪夫多项式，n为切比雪夫多项式阶数，τ是和时间相关的参数，ε是误差。

假设：需要在时间间隔［t0，t0+Δt］计算n阶切比雪夫多项式系数，其中t0为起始历元时刻，Δt为拟合时间区间的长度。首先将变量t∈［t0，t0+Δt］变换成为τ∈［-1，+1］，那么：

在切比雪夫多项式中根据如下递推公式确定Ti

根据式(1)～(3)列误差方程。求解格值系数A和切比雪夫多项式系数，完成弹簧型重力仪格值系数的精密测定。

3 gPh058重力仪测定的分析与比较

1)观测数据的预处理

观测数据的预处理，采用基于汉宁窗的FIR数字低通滤波器，对gPh058重力仪秒采样观测数据进行滤波，去除观测数据中的高频信号，按60 s间隔采样得到分钟值固体潮观测数据。利用Tsoft软件在残差的基础上对缺记部分进行补差，对地震影响数据采用线性或者3次多项式拟合，以减小或者消除非潮汐因素对残差时间序列的影响，最后恢复预处理后的分钟值固体潮观测数据［9］。预处理结果如图1(其中漂移率采用Nakai检验2天1段计算出重力仪的各时段的漂移率)。

从图1明显可以看到两台套仪器同址观测数据连续性较好。超导重力仪没有明显漂移，变幅在(-200～200)×10-8ms-2之间;而弹簧型重力仪观测数据包含了没有明显线性特征的巨大漂移(-3 000～4 000 mV)，漂移从开始观测时的250 mV/月骤变到-1 700 mV/月，仪器经过4个月的调整恢复，漂移减小到±250 mV/月。由于重力仪刚开始工作尚未稳定，出现了如图1中重力仪漂移率绝对值先增大后减小，最后平稳变化的现象。然而从开始观测到开始稳定已经经过了4～5个月的时间。

2)切比雪夫多项式阶数、采样数和采样时段对格值系数的影响分析

利用式(1)求出切比雪夫多项式阶数、采样数和格值系数的关系及切比雪夫多项式阶数、格值系数与其中误差之间的关系(图2，图2(a)中颜色的计数是利用1减格值系数后乘以1000计数得出)。

图2(a)表明当采样数较少、采用高阶切比雪夫多项式时或者当采样数过多、采用低阶切比雪夫多项式时，都无法准确测定重力仪的格值系数。图2 (b)表明采用切比雪夫多项式测定gPh058时，格值系数约为1×10-8ms-2/mV。随着多项式阶数的不断增大，格值系数趋于稳定，其中误差也逐渐减小。通过统计不同阶次格值系数的相对精度和中误差表明：当超过50阶后，gPh058重力仪的相对精度优于0.29‰，中误差优于0.45‰×10-8ms-2/mV。以上分析结果表明：利用大于50阶切比雪夫多项式的模型进行测定［4］，格值的相对精度可以优于1‰。这一分析精度和文献［5］的分析结果基本一致。

图1 gPh058重力仪和SGC053超导重力仪的同址观测数据Fig 1 Same-site observations with gPh058 gravitymeter and SGC053 superconducting gravimeter

图2 切比雪夫多项式阶数、采样数、格值系数及其中误差之间的关系Fig.2 Relations between the order of Chebyshev polynoimia，the sampling number，the scale factor and the error of mean square

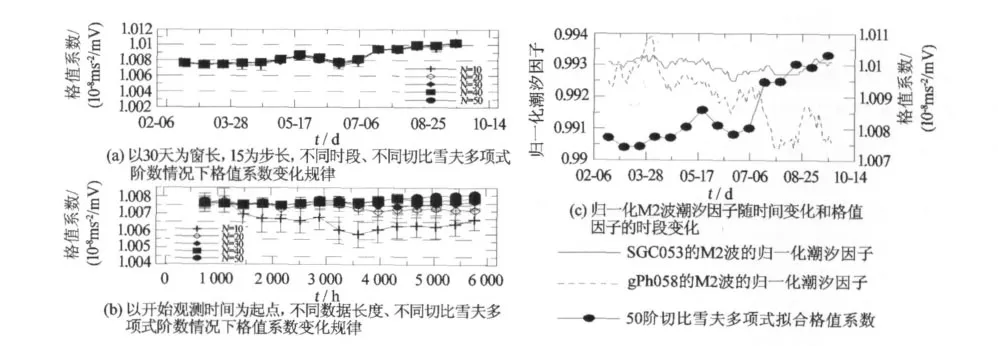
图3 切比雪夫多项式阶数、采样数、采样时段、格值系数、仪器状态之间的关系Fig.3 Relations between order of Chebyshev polynoimia，sampling number，sampling time，scale factor and instruments status

图3(a)表明，gPh058的同一时段的格值系数中误差并不随切比雪夫多项式阶数的增大而明显变化，但当利用不同采样时段的同址观测数据进行测定时，格值因子变幅最大达2.4‰×10-8ms-2/mV，这表明不同采样时段的测定数据确定的格值系数差异明显大于格值系数的中误差。图3(b)表明，越长的观测数据需要越高阶的多项式才能满足测定精度。在达到测定精度的情况下，不同采样数测定的格值系数之间最大变幅为0.4‰×10-8ms-2/mV，和采样时段相比不同采样数产生的格值系数的差异不是影响格值系数的主要因素。影响格值系数的主要因素是不同采样时段的测定数据。

3)格值系数随时段的变化分析

由于gPh058仪器首次观测，利用比测的两台套重力仪M2潮汐因子随时间变化规律来比较仪器的稳定性。图3(c)表明，和SGC053相比，gPh058重力仪在244天内M2潮汐因子一直趋向于负向变化，而这一现象和格值系数随时段的正向变化反相一至。这表明虽然仪器漂移量和漂移率已经逐渐趋于稳定，然而gPh058重力仪由于首次观测，弹簧的弹性释放没有完成，导致目前依然处于非稳定状态中，而这非稳定状态直接影响到格值的变化。因此在保证测定精度的情况下，本文对不同时段的格值系数加权平均作为gPh058的格值系数(1.008 4± 0.000 9)×10-8ms-2/mV)。

4)格值系数测定前后同址观测数据分析结果的比较

利用国际固体潮中心提供的VAV(V03.11)软件对gPh058测定前后的固体潮观测数据进行调和分析，并和SGC053的调和分析结果进行比较(表1)。

表1 gPh058重力仪和SGC053超导重力仪8个主波测定前后的调和分析结果及其比较Tab.1 Comparison among harmonic analytical results of 8 waves with gPh058 gravimeter and SGC053 superconducting gravimeter before and after determination

从上述调和分析结果可以看出，gPh058的周日和半日波的潮汐因子中误差测定前后没有发生明显变化，大约是SGC053的5倍，而校准后周日波和半日波潮汐因子都更加接近超导重力仪的潮汐因子。其中振幅较大的(大于10×10-8ms-2)的潮波(O1，K1，N2，M2，S2)不仅各潮汐因子的中误差(最大：N2波0.000 94，最小：M2波0.000 19)都优于1‰，而且相位也只有0.08°的差异。这些表明虽然gPh058的观测数据精度低于SGC053，但是利用同址观测法测定的周日和半日波的分析结果和超导重力仪的几乎一致。

图4((a)上图为测定前残差时间序列振幅谱，下图为测定后的残差时间序列振幅谱;图4(b)上图为经过校准和漂移改正后的残差时间序列;中图为漂移改正值(采用8阶傅里叶级数拟合长期弹簧漂移);下图为经SGC053观测数据改正后残差时间序列)表明测定后的重力残差时间序列的周日波、半日波振幅明显减小，约只有校准前的1/4。而且经过合成潮及其非线性函数的漂移改正后，残差时间序列的平均变幅为±7×10-8ms-2。弹簧型重力仪在这样的变幅下才有可能更好地解释外界因素对弹簧型重力仪的影响。

4 结论与讨论

1)gPh058重力仪出厂前进行过初步测定，但利用同址比测发进行测定的相对精度优于1‰，其获得的格值系数更加可靠。

2)通过分析影响同址测定方法的3个因素(采样数、采样时段和多项式阶数)，结果表明采样时段是3个因素中影响最大的。这主要是由于gPh058重力仪依然处于非稳定状态。利用不同时段的格值系数的加权均值作为gPh058重力仪的格值因子为(1.008 4±0.000 9)×10-8ms-2/mV)，格值系数的相对精度依然优于1‰。

图4 测定前后残差振幅谱(a)和测定后残差时间序列(b)Fig.4 Residual amplitude spectrum before and after determination(a)and residual time series after determination(b)

3)对gPh058重力仪观测数据进行潮汐和振幅谱分析表明：虽然gPh058重力仪的潮汐分析精度不及SGC053，但是经过精密测定后的潮汐参数更加接近SGC053。而且进行漂移和合成潮改正后，残差的周日和半日波振幅都只有测定前的1/4，而整个残差时间序列的变幅只有±7×10-8ms-2。

1 刘子维，等.gPhone重力仪数据采集系统性能的改进［J］.大地测量与地球动力学，2010，(增刊ⅡI)：102-104.(Liu Ziwei，et al.Improvement in performance of data acquisition system of gPhone gravitymeters［J］.Journal of Geodesy and Geodynamics，2010，(Supp.Ⅱ)：102-104)

2 Xu Jianqiao，et al.Investigation of the earth’s nearly diurnal free wobble resonance using tidal gravity observations with superconducting gravimeters［J］.Chinese Journal of Geophysics，1999，42(5)：599-608.

3 Micro-g LaCoste，Inc.2008 gPhone/P.E.T Hardware Manual V1.

4 Olivier Francis，et al.Calibration of the LaCoste-Romberg 906 by comparison with the superconducting gravimeter C021 in Membach(Beigium)［J］.Journal of the Geodetic Society of Japan，2001，47(1)：16-21.

5 陈晓东，等.用GWR-C032超导重力仪观测资料实施对LCR-ET20重力仪格值的精密测定［J］.测绘学报，2003，32(3)：219-223.(Chen Xiaodong，et al.Accurate determination of the scale value of the LCR-ET20 gravimeter using observations recorded with the GWR-C032 superconducting gravimeter［J］.Acta Geodaetica et Cartographica Sinica，2003，32(3)：219-223)

6 Michel Van Camp，et al.Is the instrumental drift of superconducting gravimeters a linear or exponential function of time?［J］.J Geod.，2007，81：337-344.

7 邢乐林，等.利用绝对重力测量精密测定超导重力仪的格值系数［J］.大地测量与地球动力学，2010，(1)：48-50.(Xing Lelin，et al.Scale factor calibration of a superconducting gravimeter by using absolute gravimetry［J］.Journal of Geodesy and Geodynamics，2010，(1)：48-50)

8 刘子维，等.SG-053超导重力仪的观测结果分析［J］.大地测量与地球动力学，2010，(6)：157-160.(Liu Ziwei，et al.Analysis of observations of superconducting gravimeter SG-053［J］.Journal of Geodesy and Geodynamics，2010，(6)：157-160)

9 徐建桥.重力固体潮汐理论及分析方法——武汉台超导重力仪观测资料的分析处理［D］.中国科学院测量与地球物理研究所，1997.(Xu Jianqiao.The theory and analysis of gravity tidal——superconducting gravimeter data analysis and processing in Wuhang station［D］.Institute of Geodesy and Geophysics Chinese Academy of Sciences，1997)

10 Riccardi U，et al.Comparison of the Micro-g LaCoste gPhone-054 spring gravimeter and the GWR-C026 superconducting gravimeter in Strasbourg(France)using a 300-day time series［J］.Metrologia，2011，48：28-39.

11 Smylie D E，et al.The product spectra of gravity and barometric pressure in Europe［J］.Physics of the Earth and Planetary Interiors，1993，80：135-608.

ACCURATE DETERMINATION OF SCALE VALUE OF gPh058 GRAVIMETER BY USE OF OBSERVATIONS WITH SGC053 SUPERCONDUCTING GRAVIMETER

Zhang Rui1)，Wei Jin2，3)，Liu Ziwei2，3)，Li Hui2)and Hao Hongtao2)

1)National Earthquake Infrastructure Service，Beijing 100036 2)Institute of Seismology，CEA，Wuhan 430071 3)School of Geodesy and Geomatics，Wuhan University，Wuhan430079

Using same-site observations obtained with the SGC053 superconducting gravimeter and the gPh058 gravimeter in Gravitation and Earth Tide Observatory of China(GETOC)，the scale value(alias calibration factor) of the gPh058 gravimeter is accurately determined with the Chebyshev polynomial model.Through the analysis of regression order，sampling number，sampling time，the most obvious affect factor is the sampling time.The weighted average scale factor of different sampling times is 1.008 4±0.00 09×10-8ms-2/mV.Compared with the harmonic analysis before determination，the numerical results show that tidal parameters of comparatively high accuracy can be achieved with the gPh058 gravimeter.After determination，the amplitude of the residual with synthetic tide and drift correction is only 1/4 of that as before.Although gPh058 gravimeter had been calibrated in factory，the same-site determination should be more reliable.

SGC053 superconducting gravimeter;gPhone058 gravimeter;scale factor;same-site observation; tidal parameter

1671-5942(2011)05-0151-05

2011-03-21

陆态网络应用软件研制;科技部国家社会公益研究专项(2005DIB3J120);全国重力台网学科中心运行经费(201101008);国家自然科学基金(41004030);中国地震局地震研究所所长基金(IS200956041)

张锐，男，1979年生，助理研究员，主要研究方向为GNSS及重力数据分析.E-mail：rzhang@neis.gov.cn

P315.72+6

A