不完全测量数据的 E M处理算法＊

林东方 宋迎春 金 昊

不完全测量数据的 E M处理算法＊

林东方 宋迎春 金 昊

推导了 EM算法用于不完全测量数据的实现方法。结果表明,应用 EM算法处理不完全测量数据,改善了测量精度,与完全数据下的平差结果极其接近,明显优于不进行平差处理的结果。

不完全测量数据;平差;G-M模型;最小二乘原理;EM算法

1 引言

在测量中,由于仪器设备精度、人为因素和外界环境的限制,测量中往往伴随着误差。为了保证测量的精度,将测量误差控制在一定的范围内,在必要观测的基础上常常进行多余观测,应用最小二乘原理平差计算,得到最优的估计参数。但是由于工程施工、农业生产或意外事故常常使一些控制点被破坏或找不到,无法进行观测。或者观测后,由于仪器故障、人为因素造成某些测站的观测数据被破坏或丢失。这些情况的发生,都会造成观测数据的不完整,使完全观测数据变为不完全观测数据。由于数据的不完全,在进行平差计算时就必须将破坏或丢失的数据删除之后再进行平差,这严重影响了观测质量和测量精度。当数据缺失过于严重时,就无法进行平差计算,测量数据便无法使用,观测资料也就废置不用,这就浪费了大量人力、物力和财力。

鉴于此,一些学者提出,对不完全数据进行插值处理,将缺失数据通过插值方法补充进去,而后进行平差计算,如时间序列处理的插值方法[1],这种方法虽然有一定的效果,但插值数据是对剩余数据的进一步处理所得,并没有利用更多的潜在信息。而在这方面,EM(Expectation-Maximization)算法就有着很大的优势。EM算法是用于非完全数据参数估计的一种有效方法,它是一种数据添加算法,即在观测数据的基础上添加一些“潜在数据”,利用对数据处理有益的潜在信息,得到数据缺失下参数的最优估计。当测量数据不完全时,可以利用观测数据所服从的一些规律,对缺失数据的取值范围加以限制,即采用 EM算法,利用缺失数据在现有条件下的期望值,对不完全数据进行处理计算,最终得到一个较好的参数估计结果。

2 EM算法及其在不完全测量观测数据中的处理方法

2.1 EM算法

EM算法的最大特点是通过对完全数据的处理来解决不完全数据问题[2,3]。它主要应用于下面两种不完全数据参数估计：第一,观测数据不完全,这是由于观测过程的局限性或观测后的意外事故所导致;第二,似然函数不是解析的,或者似然函数的表达式过于复杂从而导致极大似然函数难以解算。第一种情况在测量数据处理中经常遇到。

EM算法是一种迭代算法,它的每一步迭代由两步组成：E步(求期望)和M步(极大化)[4]。E步在给定己观测到的数据和现有参数下,求“缺失数据”的条件期望;M步计算参数的MLE估计,这与己知似然求参数的MLE估计的计算方法一致。

具体地讲,以 P(θ/Y)表示θ的基于观测数据的后验分布密度,称为观测数据后验分布。以 P(θ/Y, Z)表示添加数据 (缺失数据)Z后得到的关于θ的后验分布密度函数,称为完全数据后验分布。P(Z/ θ,Y)表示在给定θ和观测数据 Y下潜在数据 (缺失数据)Z的条件分布密度函数。我们的目的是计算观测后验分布 P(θ/Y)的参数。EM的算法为,记θi为第 i+1次迭代开始时后验参数的估计值,则第 i +1次迭代的两步为：

E步：将 P(θ/Y,Z)或 logP(θ/Y,Z)关于 Z的条件分布求期望,从而把 Z积掉,即

M步：将 Q(θ/θi,Y)极大化,即找一个点θi+1,使

EM算法在每一次迭代后均提高观测极大似然密度函数值,具有良好的全局收敛性[4,5]。

2.2 (G-M)模型下不完全测量观测数据的EM处理方法

测量中常采用 Gauss-Markov(G-M)模型[6]

在测量平差中,间接平差的误差方程为[7]

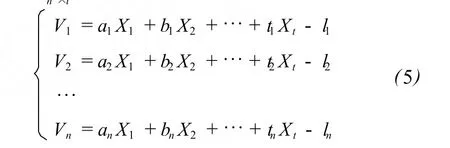
这里假设观测数据 ln由于意外事故丢失,应用 EM算法建立似然函数方程 P(θ/Y,Z)

式中θ为未知参数 X,Y为不完全观测数据 (l1,l2,…,ln-1),Z为缺失数据 ln。

由于测量误差改正数 V服从期望为零的正态分布,因此可以得到缺失数据 ln的条件分布概率密度函数为

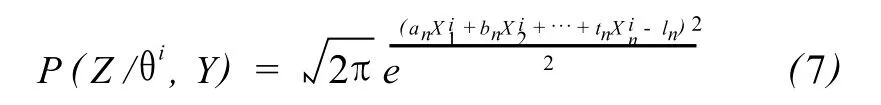
由式(6)、(7)便得到 EM算法的期望步

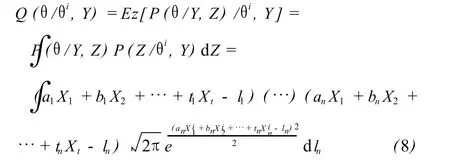
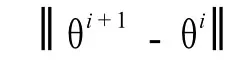
3 算例分析

以水准测量为例。在图 1中,A、B为已知水准点,其高程 HA=12.013 m,HB=10.013 m,可视为无误差,为了确定 C及D点的高程,共观测了 4个高差,h1=-1.004 m,h2=1.516 m,h3=2.512 m,h4=1.520 m。

当测量数据完全时,即高差观测值h1、h2、h3、h4没有丢失,我们采用最小二乘原理,应用间接平差法,计算得到 HC、HD的高程为：HC=11.008 3 m,HD=12.525 7 m。

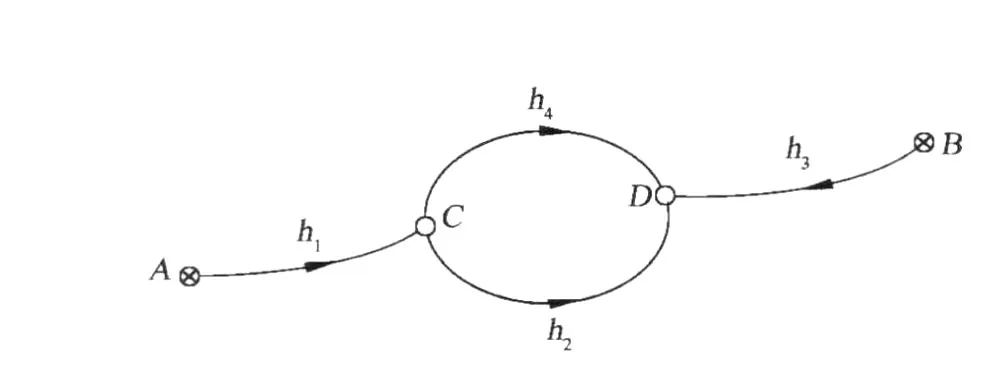
图1 水准测量路线Fig.1 Leveling line

假设由于意外事故,h2、h4数据丢失,测量数据变为不完全数据,由于 h2、h4的丢失,没有了多余观测,传统的平差方法失效,直接计算得到 HC、HD的高程为：HC=11.009 m,HD=12.525 m。

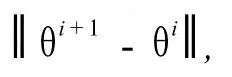
在非完全数据的情况下,两种计算方法所得结果与完全数据情况下平差计算所得结果进行比较(表 2)。不平差所得参数 HC、HD的值与完全数据下间接平差所得参数 HC、HD的值均相差 0.7 mm,而 EM算法所得参数 HC、HD的值与完全数据下间接平差所得参数值均相差 0.2 mm。由此可见,在测量数据不完全时,采用 EM算法进行数据处理能够得到更好的结果。

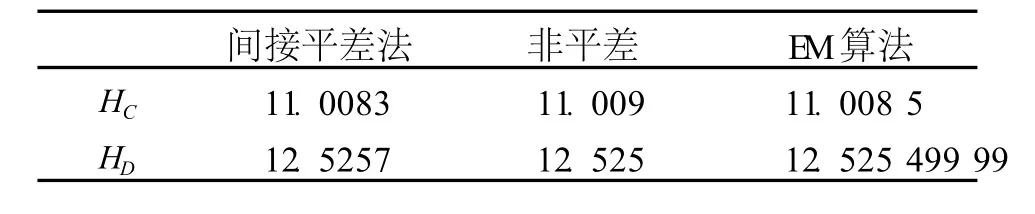
表1 高程点计算结果(单位:m)Tab.1 Elevation results(un it:m)

表2 高程点计算结果比较(单位:m)Tab.2 Comparison between elevation results(un it:m)

4 结语

推导了在测量数据不完全时,采用 EM算法进行数据处理的实现方法,通过实例,验证了 EM算法在处理不完全测量数据时的有效性。结果表明,在测量数据缺失,没有多余观测的情况下,使用 EM算法的处理结果与完全数据时平差结果极其接近,效果十分明显。在 EM算法下,许多以往废置的数据均可以重新启用,例如,往年废置变形监测数据,往年废置水准网观测数据,有了这些历史数据的加入,充分利用过去的观测数据[8],对分析高层建筑物、水坝形变,地壳形变具有不可估量的意义。

EM算法是一种迭代收敛算法,它的收敛速度较慢[9],参数初值的选取对迭代的收敛速度影响较大,因而在初值选取时,我们应利用参数的先验信息,选取一个较接近参数估计值的初值,以提高 EM算法的收敛速度。EM算法在处理单个缺失数据或连续缺失数据时的效果显著,但是 EM算法在处理重度缺失数据时,处理效果不明显[10],在处理离散缺失数据时,须分批处理,因此如何提高重度缺失数据时 EM算法的处理效果和系统整体处理离散缺失数据尚需进一步的研究。应用 EM算法要求观测值与参数之间具有一定的分布关系,当观测值与参数之间无分布关系时则不适用 EM算法。

1 武艳强,黄立人.时间序列处理的新插值方法[J].大地测量与地球动力学,2004,(4)：43-45.(Wu Yanqiang and Huang Liren.A new interpolationmethod in time series analyzing[J].Journal of Geodesy and Geodynamics,2004, (4)：43-45)

2 DempsterA P,Laird N M and Rubin D B.Maximum likelihood from incomplete data via the EM algorithm[J].Journal of the Royal Statistifcal SocietyB,1977,39：1-38.

3 钱俊,舒宁.基于 EM算法和单幅雷达图像阴影的控制点坡度校正[J].武汉大学学报 (信息科学版),2004,(12)：1 089-1 092.(Qian Jun and Shu Ning.Correction of control point slope based on EM algorithm and shading of single SAR image[J].Geomatics and Information Science ofWuhan University,2004,(12)：1 089-1 092)

4 Graham C G and Juan C A.Approximate EM algorithms for parameter and state estimation in nonlinear stochastic models [A].Proceedings of the 44th IEEE Conference on Decision and Control,and the European Control Conference[C]. 2005,12-15.

5 王兆军.EM算法收敛的必要条件[J].南开大学学报(自然科学版),1994,(2)：85-88.(Wang Zhaojun.The necessary condition on the convergence of the EM algorithm [J].Acta Scientiarum Naturalium Universitatis Nankaiensis,1994,(2)：85-88)

6 郭金运,靳奉祥,刘国林.不完全测量数据的应用研究[J].测绘通报,2002,(2)：7-8.(Cuo Jinyun,Jin Fengxiang and Liu Guolin.Study ofApplication of incomplete data in surveying[J].Bulletin of Surveying andMapping,2002, (2)：7-8)

7 武汉大学测绘学院测量平差学科组.误差理论与测量平差基础 [M].武汉：武汉大学出版社,2003.(Research Group of Surveying Adjustment,School of Surveying and Mapping,Wuhan University.The base of errors theory and surveying adjustment[M].Wuhan;WuhanUniversity Press, 2003)

8 熊俊楠,等.高层建筑物变形监测数据处理方法研究及工程应用[J].测绘科学,2010,(7)：69-71.(Xiong Junnan, et al.Research and application for high-rise deformation observation data processing method[J].Science of Surveying andMapping,2010,(7)：69-71)

9 高旅端,陈志,王家润.一种加速 EM算法收敛的方法[J].数理统计与应用概率,1998,(4)：342-348.(Gao Luduan,Chen Zhi andWang Jiarui.A method for accelerating convergence of fhe E M algorithm[J].Mathematical Statistics and Applied Probability,1998,(4)：342-348)

10 张香云,张秀伟.不同缺失率下 EM算法的参数估计[J].数理统计与管理,2008,(3)：428-431.(Zhang Xiangyun and Zhang Xiuwei. Parametrical estimation for EM algorithm in the case of different losing-rate[J].Application of Statistics and Management,2008,(3)：428-431)

EM PROCESSING ALGORITHM OF INCOM PLETE SURVEY ING DATA

Lin Dongfang,Song Yingchun and Jin Hao
(School of Geosciences and Info-Physics,Central South University,Changsha 410083)

For the incomplete surveying data caused by various factors,traditional adjustment can not be achieved.It is har mful to the accuracy of the surveying,even leads to abandoned observation data.Through EM algorithm,we can take the potential infor mation which is helpful to i mprove the accuracy of data processing effectively.EM processing algorithm for incomplete surveying data is proved.The results show that the surveying accuracy is improved by using the EM algorithm to process the incomplete data.The results are extremely si milar to the adjustment resultswith complete data and significantly better than the resultswithout adjustment.

incomplete surveying data;adjustment;G-M model;principle of least squares;EM algorithm

(中南大学地球科学与信息物理学院测绘与国土信息工程系,长沙 410083)

1671-5942(2011)04-0112-04

2011-01-16

国家自然科学基金 (40874005);教育部博士点基金(200805331086)

林东方,男,1986年生,硕士研究生,主要研究方向为现代测量数据处理.E-mail：lindongfang223@163.com

P207;P203

A