基于阶次组合的 GPS精密星历插值研究＊

王晓明 成英燕 刘 立

(中国测绘科学研究院,北京 100039)

基于阶次组合的 GPS精密星历插值研究＊

王晓明 成英燕 刘 立

(中国测绘科学研究院,北京 100039)

采用Lagrange插值与线性逐次Neville插值两种方法对 GPS卫星轨道进行了插值,比较了两种方法的特性及插值精度,结果表明两种方法虽然简单易实现,但当进行高阶插值时,边缘插值区间的精度较低。为解决该问题提出利用高次插值与低次插值相结合的方法进行轨道插值,算例证明,该插值方法可以改善插值精度。

GPS;精密星历;Lagrange插值;Neville插值;不同阶次

1 引言

GPS定位以站星间的距离观测量为基础,以卫星位置为动态已知点进行空间后方交会,因此要正确获取卫星的坐标是 GPS定位中的一个重要问题。目前应用的卫星星历主要有广播星历和精密星历两种。广播星历属于实时星历,精度较低,无法满足高精度定位的需要。精密星历精度较高,通常情况下可以达到 5 cm的精度。由于 IGS提供的精密星历为 15分钟间隔,但在实际应用中需要的数据密度通常要比这大的多。因此在 GPS数据处理中,对精密星历进行高精度、高效率的内插或者拟合已成为一项十分必要的工作。目前,较常用的插值方法有Lagrange插值及逐次 Neville插值[1-6]。这两种方法较为简单,算法易实现。但由于两种插值方法本身所具有的缺陷使得插值结果存在龙格现象,而目前解决该问题的方法是采用其他时段的数据对边缘区间进行重新插值以提高精度,这就不可避免地制约了这两种方法的实用性。本文在分析两种插值方法特点的基础上,比较了不同阶次的插值多项式的插值精度,以寻求用低阶插值与高阶插值的组合方法来获取精度更高、更稳定的插值结果。

2 插值的数学模型

1)Lagrange插值

假设有 n+1个节点时刻,分别为 t0,t1,…,tn,对应时刻的星历依次为 y0,y1,…,yn,利用 Lagrange对星历进行 n阶多项式插值[6]：

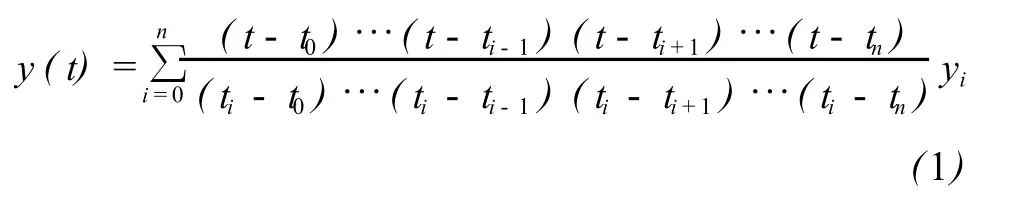
2)逐次 Neville插值

在进行星历插值研究过程中,若发现低阶插值多项式的插值精度不能满足要求时,通常需要采用增加节点的方法进行重新插值。若插值的数据量较大,势必会使插值效率受到影响。而 Neville插值方法通过改善算法使该问题得到解决,其基本的插值算法思路为[4]：设有 n+1个节点时刻 t0,t1,…,tn,其对应的精密星历为 y0,y1,…,yn。令

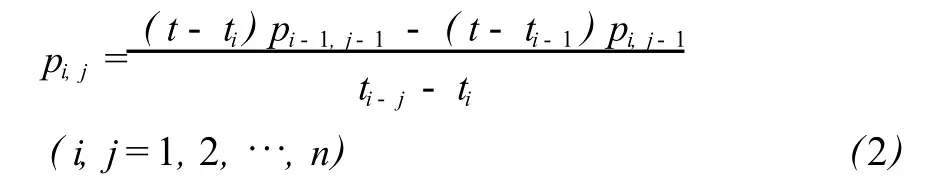
计算流程见表1。

表1 Neville算法流程Tab.1 Flow chart of Neville algorithm

从表 1可以看出,当精度不满足要求,需再增加一个节点时,前面的计算完全有效。Neville算法的该特性也使得计算的效率更高。但两种插值存在自身算法上的局限性,即当采用高阶的插值多项式时,插值边缘区域的插值精度会出现抖动。本文将通过实例计算判断产生抖动的插值区间,并通过采用低阶与高阶相组合的插值方法来获得整个区间的高精度的插值结果。

3 算例分析

本文首先随机采用 PRN4卫星 2002年 1月 1日的精密星历数据,采用 Lagrange及Neville两种插值方法,插值弧段取为 12小时,将 15分钟间隔的实验数据进行插值得到 5分钟间隔的数据结果,并将结果同给出的真值数据比对,以得出相应的结论;然后,在该结论的基础上进行基于阶次组合的插值研究,以期改善插值精度,提高插值结果的稳定性。

3.1 基于无阶次组合下两种插值结果的精度比较

基于无阶次组合的情况下,采用两种插值方法,进行 14～23阶的插值实验,插值结果如表 2所示。

由表 2可以看出,利用Lagrange插值法与 Neville插值法进行 12小时弧段的插值时,两种插值方法的插值精度基本相同,且插值阶数取 18～20阶时都能得到较好的插值精度,x、y、z3个方向的插值标准差均小于 1 cm。但同时由于两种插值方法本身的局限性,使得高阶插值的边缘精度较低,且表格中的插值残差最大的点均出现在边缘区间,因而本文提出在边缘处采用低阶插值的方法以改善该种情况。为得出需要进行重新低次插值的时间段,我们给出利用两种插值方法,采用插值阶数为 20时的插值残差,结果如图 1所示。

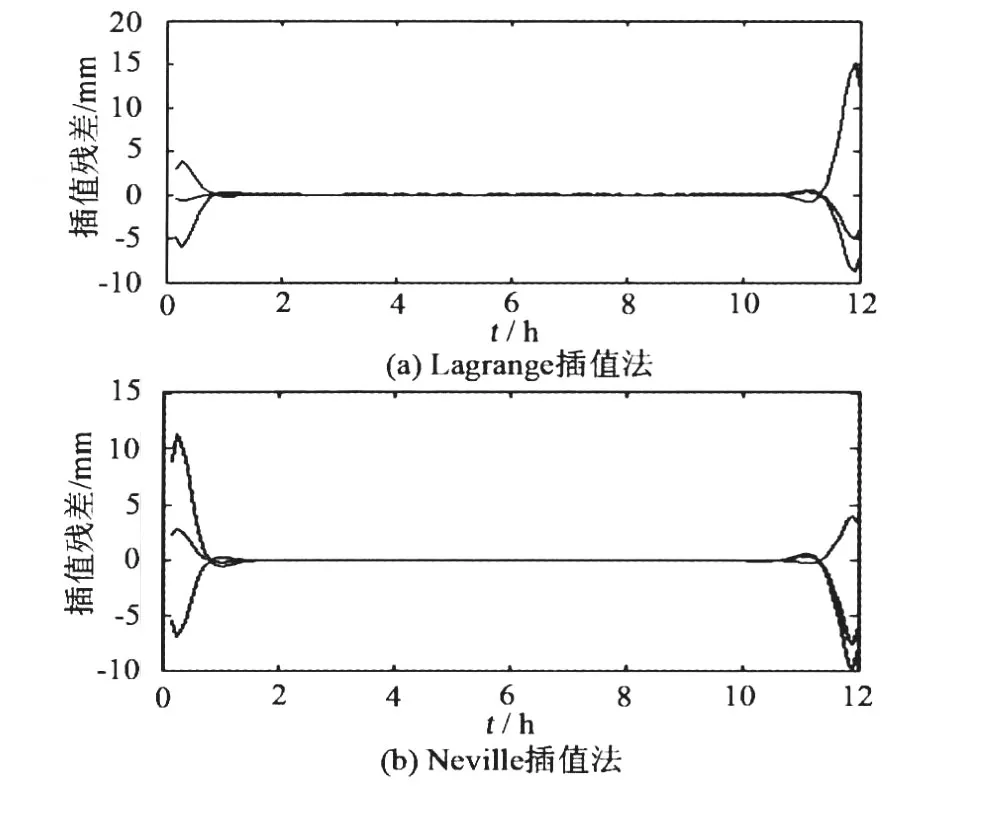
图1 20阶插值残差Fig.1 Interpolation residuals of 20th order

由图 1可以看出,利用 Lagrange或 Neville插值法采用较高阶插值方法时,会出现所谓的龙格现象。为提高边缘部分的插值精度,通常可以采用拼接前一天的数据进行插值。但在只有一天数据的情况下,我们则尝试采用低阶插值与高阶插值相组合的方法改善边缘部分的插值精度。

3.2 基于阶次组合下的两种插值方法的精度比较

从计算结果可以看出,3～10小时区间的插值误差均小于 1 mm,因而选取 0～2与 10～12小时作为重新计算的插值区间。具体计算过程是采用低阶Lagrange或Neville插值方法对 0～2小时和 10～12小时的弧段进行插值,中间弧段仍采用高阶插值结果。具体算法为：采用 0～3小时的数据,分别采用8、9、10阶插值多项式对 0～2小时弧段进行重新插值计算,采用 9～12小时数据,同样方法对 10～12小时的数据进行重新插值计算。利用插值结果取代原有结果,并依据新数据重新计算 0～12小时区间的插值残差。同时增加 PRN21卫星进行计算,以验证结论是否具有普遍性。结果如表 3所示。

由表 3可以看出,在采用 10阶与 20阶组合的Lagrange与 Neville插值方法时,插值精度有了明显提高,最大插值残差也小于 0.02 mm,可以满足高精度的定位需要。因此在实际工程中若需要高精度的插值结果,且只有一天的星历数据的情况下,则可以采用高阶与低阶插值多项式相组合的方法进行星历插值。图 2是利用 Lagrange插值方法,采用两种阶次结合的插值方法,分别对 PRN4卫星及 PRN21卫星星历插值得出的残差结果。

由图 2可以看出,采用不同阶次组合插值可以很好地改善由于高阶插值多项式不稳定性所带来的龙格现象。

4 结论

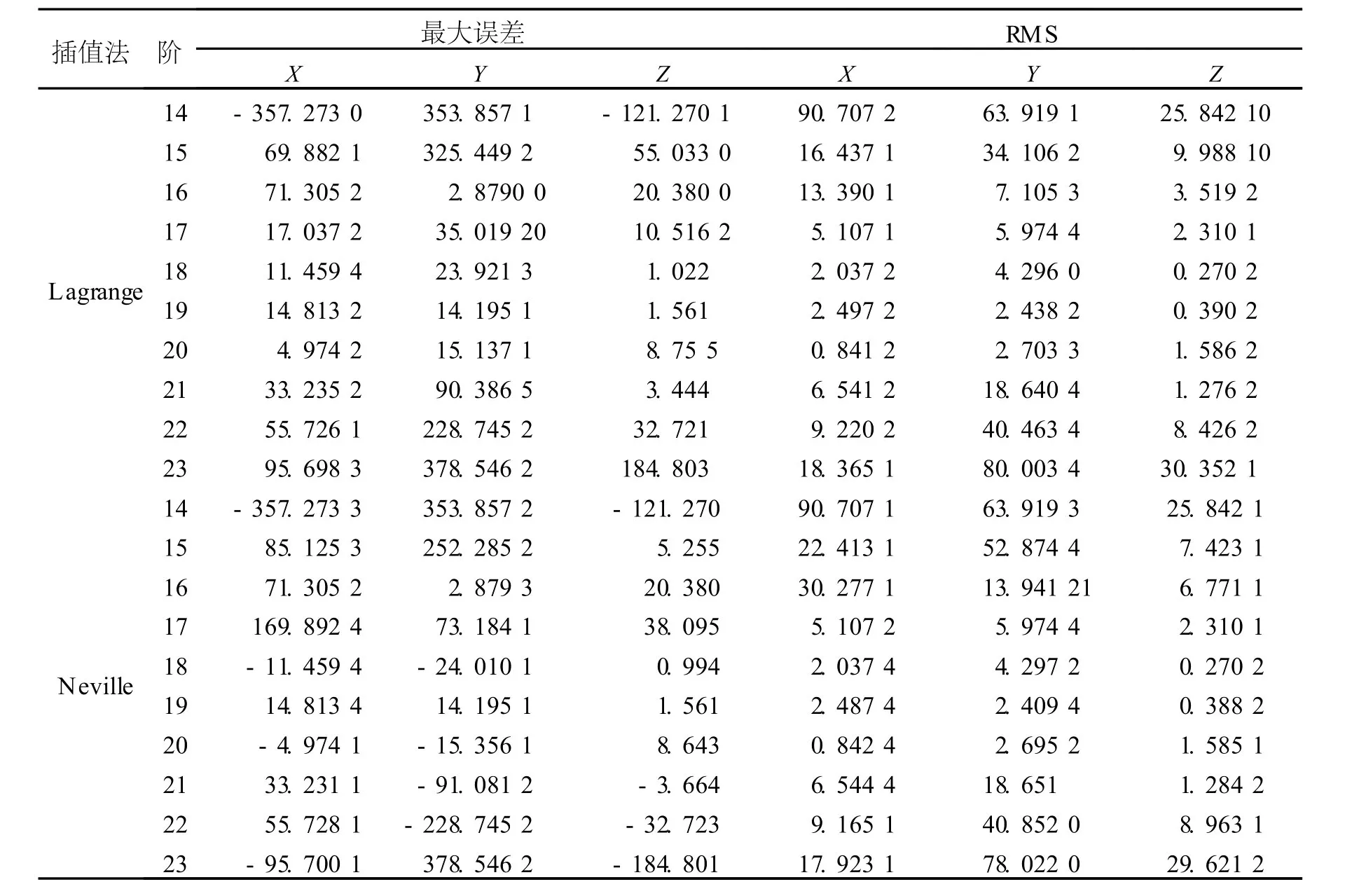
表2 不同阶次的多项式内插结果(单位:mm)Tab.2 I nterpolation results of different order(un it:mm)

表3 不同阶次的多项式内插结果(单位:mm)Tab.3 Interpolation results of different orders(un it:mm)

1)Lagrange与 Neville插值方法的本质是一致的,两者的插值精度具有高度的一致性。对于 12小时弧段的数据,两种方法采用 18～20阶插值多项式时取得的插值精度最高。

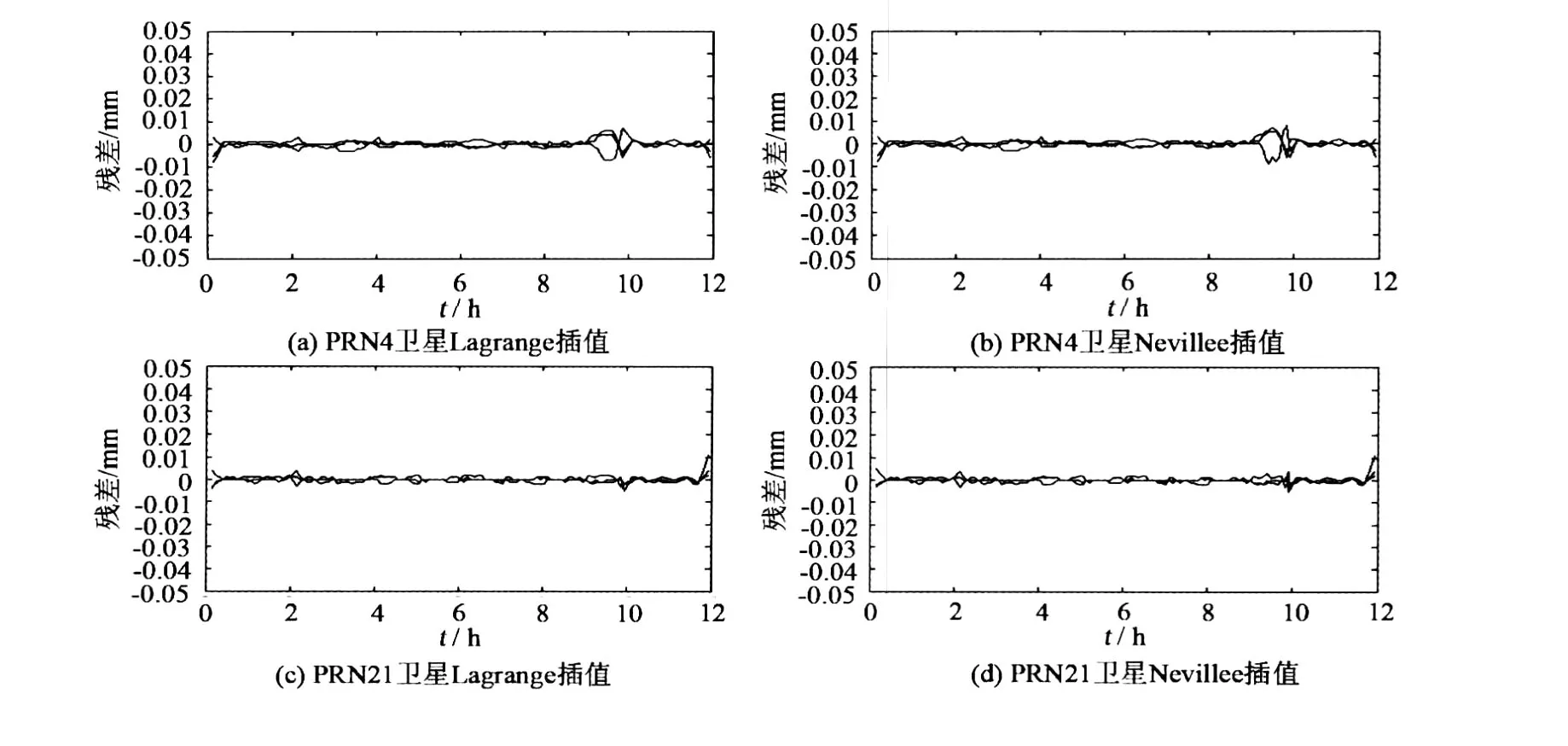
图2 插值残差Fig.2 Interpolation residualswith new method

2)Neville较 Lagrange来说,其插值效率更高,更加适合在计算机上进行自动计算。

3)在采用高阶插值时,两种方法都存在龙格现象,即插值的边缘部分的精度较低,且存在一定的震荡性,这是两种方法在采用高阶多项式进行插值时的固有弊端。

4)对于插值弧段的边缘部分采用低阶插值多项式,中间仍采用高阶插值多项式可以很好地改善插值精度,例如 12小时插值弧段,在 0～2小时及10～12弧段采用 10阶插值多项式,2～10弧段采用20阶插值多项式时,插值精度相当高,所有插值残差均小于 0.02 mm,足以满足高精度的定位需要。且该种方法改善了采用单一的高阶多项式插值所产生的不稳定性,Lagrange与 Neville两种方法的插值精度仍是一致的。

1 李明峰,江国焰,张凯.IGS精密星历内插与拟合法精度的比较[J].大地测量与地球动力学,2008,(2)：77-80. (Li Mingfeng,Jiang Guoyan and Zhang kai.Comparison of interpolating and fitting IGS precise ephemeris[J].Journalof Geodesy and Geodynamics,2008,(2)：77-80)

2 冯炜,等.两种常用 GPS星历拟合方法的精度分析[J].大地测量与地球动力学,2010,(1),145-149.(Feng Wei,et al.Accuracy assess ment of two fitting methods for GPS precise ephemeris[J].Journal of Geodesy and Geodynamics,2010,(1),145-149)

3 洪樱,欧吉坤,彭碧波.GPS卫星精密星历和钟差三种内插方法的比较 [J].武汉大学学报 (信息科学版),2006, 31(6)：516-518.(Hong Yin,Ou Jikun and Peng Bibo. Three interpolation methods for precise ephemeris and clock offset of GPS satellite[J].Geomatics and Information Science ofWuhan University,2006,31(6)：516-518)

4 魏二虎,柴华.GPS精密星历插值方法的比较研究[J].全球定位系统,2006,5：13-15.(Wei Erhu and Chai hua. The comparison research on GPS precise ephemeris interpolation methods[J].GNSS World of China,2006,5：13-15)

5 陈鹏,陈正阳,李骁.一种新的 GPS精密星历插值方法[J].大地测量与地球动力学,2009,(2)：111-114. (Chen Peng,et al.A new method for GPS precise ephemeris interpolation[J].Journal of Geodesy and Geodynamics, 2009,(2)：111-114)

6 张守建,等.两种 IGS精密星历插值方法的比较分析[J].大地测量与地球动力学,2007,(2)：80-83.(Zhang Shoujian,et al.Comparative analysis on two methods for IGS precise ephemeris interpolation[J].Journal of Geodesy and Geodynamics,2007,(2)：80-83)

RESEARCH ON GPS PREC ISE EPHEM ERIS INTERPOLATI ON BASED ON HIGH/LOW ORDERS INTEGRATED

Wang Xiaoming,Cheng Yingyan and Liu Li
(Chinese Academ y of Surveyingamp;M apping,B eijing 100039)

Both the characteristics of Lagrange interpolation and Neville interpolation are compared with each other.It is concluded from the results that the high-order interpolation is not good enough for high-precise applications.Finally,a new interpolation method which based on high/low orders to solve this problem is put forth.

GPS;precise ephemeris;Lagrange interpolation;Neville interpolation;different orders

1671-5942(2011)04-0103-04

2011-02-15

国家基础测绘项目(B2551)

王晓明,男,1988年生,硕士生,主要研究方向为空间大地测量数据处理的理论与方法.E-mail：chwxm@sina.cn

P207

A