地形变应变张量矩阵的不变量分析*
2011-11-23刘序俨季颖锋黄声明梁全强
刘序俨 季颖锋 黄声明 梁全强
地形变应变张量矩阵的不变量分析*
刘序俨1)季颖锋1,3)黄声明1)梁全强2)
在给出正交曲线坐标系的有关位移向量及其全微分、位移梯度矩阵、应变张量矩阵的普适表达式的基础上,又给出了任意两种正交曲线坐标系下的应变张量矩阵的普适转换表达式,并指出:由于该变换矩阵为正交矩阵,故应变张量矩阵为相似矩阵。并对应变张量矩阵的几何物理性质进行了分析,指出任何一种正交曲线坐标系的应变张量矩阵都具有唯一不变的主应变特征多项式,由该矩阵的主应变特征值方程皆可求得地壳质点处的主应变及其主方向,由主方向单位向量又可把该矩阵化为以主应变为对角元素的对角矩阵,该矩阵及其对角矩阵的迹皆为该质点处的体应变,该矩阵的行列式等于该质点处 3个主应变的乘积,这些几何物理量皆为该质点处的地应变不变量。
位移向量;位移梯度矩阵;应变张量矩阵;普适表达式;几何物理不变量
1 概述
应变与旋转是地壳运动的一种表现形式。地壳运动是指组成地壳介质的质点位置不断发生相对变化的一种现象,质点位置的变化称为位移,在单位时间内发生的位移称为地壳运动速率。对于刚体,由于其中任意两点间的距离保持不变,在外力作用下,刚体可能发生整体平移或旋转,但绝不会发生变形。但实际上,地壳既不是刚体,也不是流体,而是介于两者之间的一种弹性介质。在外力作用下,地壳质点位移体现为地壳介质对该作用力的一种响应,包括平移、旋转和应变[1,2]。
由地壳质点位移所引起的平移、旋转与应变构成了地形变的 3种要素。在构成地形变的 3种要素中,平移代表质点从A挪至B,旋转与应变则一起表征了该质点处的变形,旋转与应变分别为位移梯度矩阵的不同组合。人们不禁要问,位移梯度矩阵的几何意义何在?为什么应变与旋转矩阵皆可表征为该矩阵的组合,其几何物理含义是什么,不同坐标系下的这两个矩阵的转换关系又是怎样的,在不同坐标系下的旋转和应变矩阵元素值都不相同,为什么说两者是等价的,其等价的内涵和外延是什么,它们所表征的几何物理特征又是什么?在对地壳形变位移观测资料进行应变分析时,如何选择坐标系,又如何求得位移分量对坐标变量的偏导数呢?这些问题正是本文要探讨的主要内容。
2 应变张量矩阵表达式
地壳介质的位移是该质点对外力作出的一种响应,而位移向量的空间变化率则刻画了地壳介质的应变。地壳质点的位移向量的空间变化率可由该质点的位移梯度矩阵取得[3],位移梯度矩阵在任一正交曲线坐标系中的普适表达式为:

地壳质点的位移梯度矩阵 E及转置矩阵 ET之和的 1/2,给出了该质点位移在其邻域所产生的地壳介质的应变张量矩阵[1,3],其普适表达式为:

其中
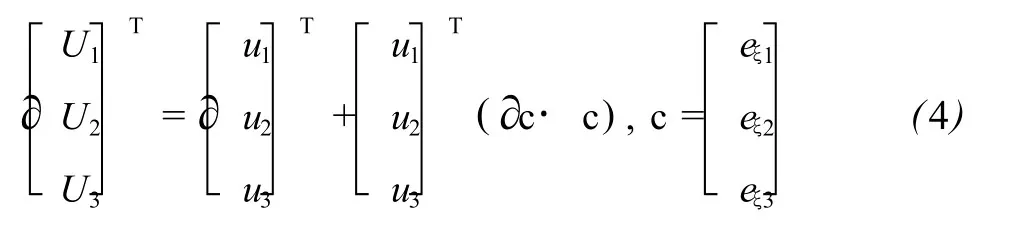
式(4)中的[U1U2U3]为地壳质点处的位移向量的全微分在该质点处的正交单位标架上的分量,[u1u2u3]为位移向量在坐标标架上的分量,[eξ1eξ2eξ3]为在该项质点处的正交曲线坐标系的正交单位标架[4]。地壳质点处的应变张量矩阵取决于该质点处的坐标标架,在不同的坐标系下有不同的表达式,但不管怎样,由不同坐标系给出的地壳变形都是唯一的,这就牵涉到应变张量矩阵的性质。

3 应变张量矩阵及其性质
式(2)给出了地壳某一质点处的应变张量矩阵的普适表达式,不论由哪种正交曲线坐标系下的应变张量矩阵都能刻画出地壳质点处的位移所引起的任何一个方向的线应变以及由该点处两个方向间的角度改变量(剪应变),因为在该点处的应变张量矩阵已包含了该点处局部变形的所有信息。设 eξ为该点处某一方向ξ相对于该点处的单位标架的单位向量,则该方向上的线应变εξ可由[1,5]

求出。又设η为该点处的另一方向,其相对于该点处的单位标架的单位向量为 eη,那么由 eξ和 eη两个单位向量所构成的角度改变量εξη(以弧度为单位)可由[5]

求出。若 eξ⊥eη,则εξη就是ξ η平面上的剪应变。
不同坐标系的应变张量矩阵如同这两个坐标系的单位标架一样可以相互转换,设 (M:eAξ1,eAξ2, eAξ3)与 (M:eBu1,eBu2,eBu3)分别在 M点在 A与 B坐标系下的单位活动标架,则这两个坐标系的应变张量矩阵εA和εB的相互转换表达式为[1]:
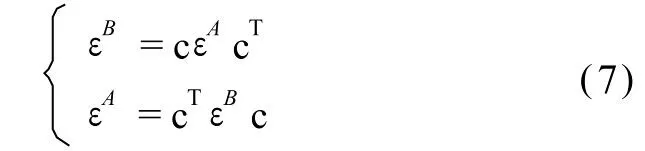
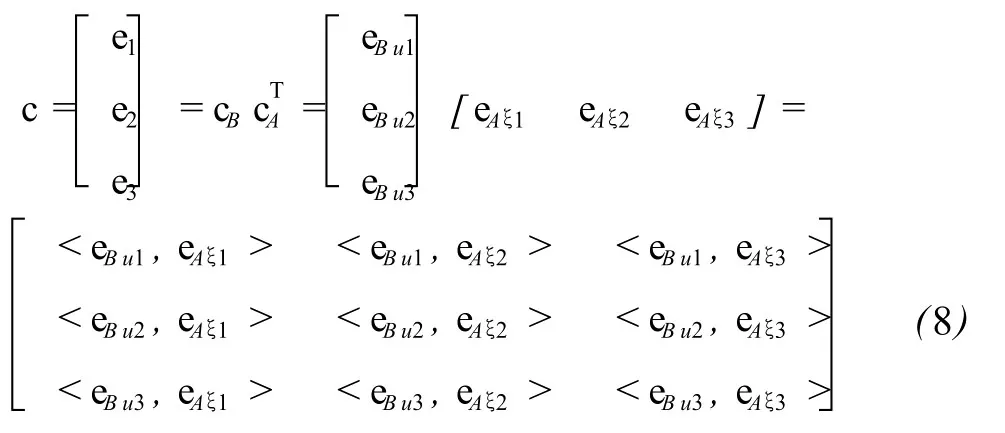
式中,eBu1,eBu2,eBu3与 eAξ1,eAξ2、eAξ3可由 M点在 B与A坐标系中的位置向量表达式求得[4,5]。由于 cB和cA皆为正交矩阵,故 c亦为正交矩阵[1]。

其中,cik为转换矩阵 c中第 i行第 k列的元素。按定义,与这些分量即为张量,与是其指标记号,εA和εB是其整体记号[1]。
4 应变张量矩阵的不变量分析
按弹性力学,通常在剪应变为零的平面上,正应变会取得极大值和极小值,也就是所谓的主应变[1,2,6,7],主应变实际上是应变张量矩阵的特征值。这些特征值所属的方向称为特征向量的方向,亦即主方向[1,2,6,7]。在地壳某质点处所产生的主应变及其主方向与坐标系的选择无关,是该质点变形的一种不变量,这是因为在式(7)中,联系A坐标与B坐标系下的两个应变张量矩阵εA和εB之间的变换矩阵 c为正交矩阵,因此εA和εB为相似矩阵[8-10]。在这里,“相似”一词是指在不同坐标系下的所有应变张量矩阵都是等价的,虽然,在不同坐标系下应变张量矩阵元素数值各不相同,但它们却都隐藏着与坐标系选择无关的地壳某质点处地壳局部变形的某些几何物理不变量,这正是等价或相似概念的内涵,而不同坐标系下,因该质点处的局部标架各不相同,因而各自的矩阵元素数值也各不相同,正是该概念的外延。根据线性代数理论[8-10],不难证明,不同坐标系下应变张量矩阵隐藏着在该质点处局部变形的某些几何物理不变量,挖掘出这些几何物理不变量,可以加深我们对应变张量矩阵特性的认识,这些几何物理不变量分别为:
1)应变张量矩阵具有相同的主应变特征值多项式
设λ为主应变,则应变张量矩阵ε的特征值方程为:

式中 I为三阶单位矩阵,式(10)的展开式为:

其中:
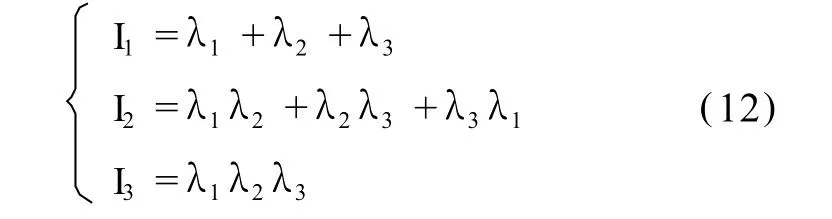
由于在地壳某质点处的主应变是一个几何不变量,故 I1、I2、I3亦皆为不变量。
设λi为应变张量矩阵的某一主应变,ξi为该主应变对应的特征向量(主方向),则ξi可由矩阵特征值方程求出;

2)应变张量矩阵的行列式等于主应变乘积,为一常数

3)应变张量矩阵皆可表达为对角线元素为主应变的对角张量矩阵
由于实对称矩阵的特征值皆为实数,设λ1、λ2、λ3分别为该矩阵互不相等的特征值 (主应变),ξ1、ξ2、ξ3分别为各其所对应的单位特征向量 (主方向),则这 3个特征向量必相互正交,则把该矩阵转换为对角矩阵的转换矩阵为 c=(ξ1,ξ2,ξ3),由此可得以主应变为分量的对角应变张量矩阵ελ为

若λ1、λ2、λ3有两个是重根,此时可对重根所对应的两个特征向量分别做施密特正交化[8-10],以取得单位正交基,即单位特征向量。
若λ1=λ2=λ3=λ,此时不存在主应变与主方向,地壳质点在任何方向受力情况与静止流体中质点受力一样,把与该力大小相等方向相反的力称为静水压力,设静水压力为 P,地壳介质体积模量设为B,由文献[7,12-15],则在该质点处的体应变为:

4)应变张量矩阵的迹为体应变且为一常数
根据弹性力学理论[1],应变张量矩阵的迹等于该点处的体应变,故
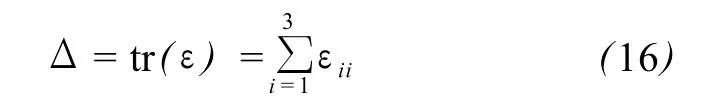
把应变张量矩阵对角化以后,其对角矩阵的迹为主应变之和,该和即等于体应变Δ[1,4]

根据向量场理论[16],体应变又可表达为:

式中 u为该质点的位移向量,▽为哈密顿微分算子,其表达式为
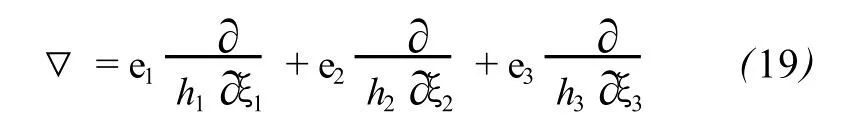
顾及到式 (4),则式 (17)变为:
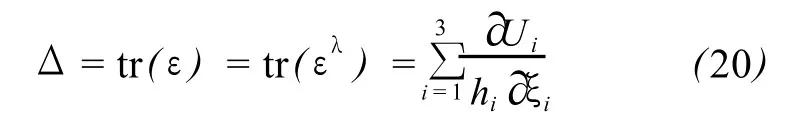
5 认识与讨论
在给出正交曲线坐标系下的有关位移梯度矩阵、应变张量矩阵的普适表达式的基础上,给出了任意两种正交曲线坐标系下的应变张量矩阵的普适表达式,对位移梯度矩阵的几何物理性质进行了较为详细的分析,并着重指出因在正交曲线坐标系中,局部单位坐标标架的转换矩阵是正交的,因此应变张量矩阵为相似矩阵。在此基础上,对应变张量矩阵的几何物理性质进行比较深入的分析,并指出隐藏在应变张量矩阵中的这些地形变不变量正是相似矩阵等价概念的内涵,而不同坐标系下的应变与旋转张量矩阵元素具有不同数值正是该项概念的外延。
应变与旋转张量矩阵皆为位移梯度矩阵及其转置的不同组合,因此,位移梯度矩阵既刻划地壳某一质点处所有的地应变信息,又给出该质点处的地壳刚体旋转方向及其旋转角位移,即给出了该质点处的空间应变率。
既然不同正交曲线坐标系的应变张量矩阵可以相互转换[4],那么到底使用哪种坐标系下的应变张量公式进行应变分析好呢?这要视观测资料而定。如果采用在WGS84坐标框架下的 GPS观测资料计算应变时,文献[17]建议,即使在小范围内也应采用球坐标系应变张量公式,而不应使用平面坐标系的应变张量公式,以免引入系统误差,因为该文认为“球面上的垂直位移可以产生径向和纬向的正应变,径向位移可以产生纬向的正应变,纬向位移也可以产生剪应变”。特别在研究面积大、时间跨度长,位移量大的情况下更是必需的,当然,在这种情况下采用文献[18]给出的椭球面上的应变张量公式较好,因为此时顾及WGS84椭球面上的曲率,比球面更为精密。
如果在 IFRF框架对地壳形变进行应变分析,则不需顾及地球曲率,因为 x、y、z这 3个直角坐标观测值本身就内蕴了地球曲率信息,此时可采用空间直角坐标系的应变公式进行应变分析,在顾及了地球曲率情况下,无论是采用直角坐标系,还是球面抑或椭球面坐标系应变公式所得到的应变张量在理论上都是等价的,因为他们之间的数值可以相互转换。
在取得诸测站的位移观测资料后,是否就可直接按式(2)进行地应变分析呢?回答是否定的,究其原因是除天体起潮力引起的空间变化率可知外[19-22],在一般情况下,我们无法得知观测点的位移坐标函数表达式,但在这种情况下,如何解决应变张量计算呢?为此,许多学者进行了探讨[23-25],虽然这些探讨在某些方面有所不同,但总的来说都是以若干个观测点作为支撑点来确定某个内插函数,在进行内插时,如果没有给观测值提供一种假定的动力学模型数据的话,那么,采用纯粹的几何模型内插方法必须满足观测点的分布密度能保证相邻观测点之间的线性内插达到足够的精度以满足研究的需要,以及所选定的几何内插函数能确保相邻观测点之间存在近似线性内插关系,内插函数可采用样条逼近技术或拟合推估方法求得。在求取旋转张量矩阵时,也面临同样的困境,但也是采用上述相同的方法予以解决,见文献[26]。
1 王敏中,王炜,武际可.弹性力学教程[M].北京:北京大学出版社,2002.(WangMinzhong,WangWei andWu Jike. The course of elastic mechanics[M].Beijing:Beijing University Publishing House,2002)
2 米恩斯著,丁中一译,王仁校.应力与应变[M].北京:科学出版社,1982.(W D Means.Stress and strain[M]. Springer-VerlayNew York,Inc,1976)
3 牛滨华,孙春岩.固体弹性介质与地震波传播[M].北京:地质出版社,2005.(Niu Binhua and Sun chunyan.Solid elastic medium and seismic wave trans mit[M].Beijing:Geologic Press,2005)
4 刘序俨,季颖锋,梁全强.正交曲线坐标系应变张量的普适表达[J].大地测量与地球动力学,2008,(4):89-96. (Liu Xuyan,Ji Yingfeng and LiangQuanqiang.Expression of strain tensor in orthogonal curvilinear coordinates[J].Journal of Geodesy and Geodynamics,2008,(4):89-96)
5 刘序俨,黄声明,梁全强.正交曲线坐标系的应变张量转换[J].大地测量与地球动力学,2008,(4):71-76.(Liu Xuyan,Huang Shengming and Lian Quanqiang.Conversion of strain tensor matrice between two orthogonal curvelinear coordinates[J].Journal of Geodesy and Geodynamics,2008, (2):71-76)
6 杨W C,布迪纳斯编.岳珠峰,等译.罗式应力应变公式手册[M].北京:科学出版社,2005.(YoungW C and Budynas R G.Roak’s for maulas for stress and strain(7th Edition).NewYork:Oxford,etc.McGraw-Hill Companies Ins, 2005)
7 Jaeger J C.Elasticity fracture and flow[M].Lodon:Methuem amp;CO.Lto.New York:Johnwi-Leyamp;Sows.I NC.1964)
8 俞正光,林润亮,鲁自群.线形代数与几何[M].北京:清华大学出版社,2009.(Yu Zhengguang,Lin Runliang and Lu Ziqun.Linear algebra and geometry[M].Beijing:Tsinghua University Press,2009)
9 同济大学数学系编.线性代数及应用[M].北京:高等教育出版社,2008.(Edited by Department ofMathematics of TongjiUniversity.Linear algebra and it’s application[M]. Beijing:Advanced Education Press,2008)
10 戴明强,刘子瑞编.工程数学 (上册)[M].北京:科学出版社,2009.(Dai Mingqiang and Liu Zirui.Engineering mathematics(1st Volume)[M].Beijing:Science Press, 2009)
11 Christopher Clapham.Oxford concise dictionary of mathematics[M].Shanghai:Shanghai Foreign Language Education Press,2001.
12 Paul P U.College physics[M].Beijing:Mechanical Industry Press,2003.
13 傅承义,陈运泰,祁贵仲.地球物理学基础[M].北京:科学出版社,1985.(Fu C Y,Chen Y T and Qi G Z.Foundation of earth physics[M].Beijing:Science Press,1985)
14 John Wahr.Geodesy and gravity[M].Samizdat Press, 1996.
15 刘序俨,等.承压井水位观测系统对体应变的响应机制分析[J].地球物理学报,2009,52(12):3 147-3 157. (Liu Xuyan,et al.Response analysis of the well-water system in cinfined aquifer[J].Chinese Jourual of Geophysics,2009,52(6):1 389-1 401)
16 Greenberg M D.Advanced engineering mathematics(The 2nd edition)[M].Beijing:Publishing House of Electronics Industry,2004)
17 石耀霖,朱守彪.用 GPS位移资料计算应变方法的讨论[J].大地测量与地球动力学,2006,(1):1-6.(Shi Yaolin and Zhu Shoubiao.Discussion on method of calculation strain with GPS displacement data[J].Journal of Geodesy and Geodynamics,2006,(1):1-6)
18 刘序俨,黄声明,梁全强.旋转椭球面上的应变与旋转张量表达[J].大地测量与地球动力学,2007,(3):240-249.(Liu Xuyan,Huang Shengming and Liang Quanqiang. Expression of strain and rotation tensor in Geodetic coordinates[J].Journal of Geodesy and Geodynamics,2007, (3):240-249)
19 北京大学地球物理系,武汉测绘学院大地测量系,中国科学技术大学地球物理教研室主编.重力与固体潮教程[M].北京:地震出版社,1982.(Department of Geophysics ofBeijing University,Depart ment of Geodesy ofWuhan Institute of Surveying andMapping,Teaching and Reseasch Group Of Geophysics of China Science and TechlologyUniversity.Course of gravity and earth tide[M].Beijing:Seismological Press,1982)
20 梅尔基尔著,杜品仁,吴庆鹏,陈益惠,刘克人译.行星地球的固体潮[M].北京:科学出版社,1984.(Melchior P. Translated byDu Pinren,et al.The tides of the planet earth [M].Beijing:Science Press,1984)
21 vanicek P and Krakiwsky E J.Geodesy:The concepts[M]. New York:Elsevier Science Publishing company,I NC. 1986.
22 刘序俨.应变固体潮主应变及剪应变计算——四川姑咱应变固体潮分析[J].地球物理学报,1994,37(Supp.1):213-221.(Liu Xuyan.Analysis on earth strain tide of Guza sesmiostation[J].Acta Geophysica Sinica,1994,37 (Supp.Ⅱ):213-221)
23 Altiner Y.Analytical surface deformation theory for detection of the Earth’s crust movement[M].Berlin:Heidelberg,etc.Springer-Verlag,1999,1-70.
24 瓦尼切克主编,黄立人,孙铁珊,张中伏译,陈鑫连校.四维大地测量定位 [M].北京:地震出版社,1990.(Vanicek P.Four-dimensional geodetic positioning[M].I AG SSG 4.96,Springer International,1987)
25 吴云,等.用 GPS观测结果对中国大陆及邻区现今地壳运动和形变的初步探讨[J].地震学报,1999,21(5):545 -553.(Wu Yun,et al.Primary research of crustal movement of China’s continent and it’s adjacent area by ussing GPS observation data[J].Acta Seismologica Sinice,1999, 21(5):545-553)
26 刘序俨,黄声明,林岩钊.地形变旋转张量探讨[J].大地测量与地球动力学,2010,(5):57-63.(Liu Xuyan, Huang Shengming and Lin Yanzhao.Research on rotation tensor of crustal defor mation[J].Journal of Geodesy and Geodynamics,2010,(5):57-63)
ANALYSIS OF INVARIANTS IN STRA IN TENSOR MATRIXES OF CRUSTAL DEFORMATI ON
Liu Xuyan1),Ji Yingfeng1,3),Huang Shengming1)and LiangQuanqiang2)
(1)Earthquake Adm inistration of Fujian Province,Fuzhou 350003 2)Xianm en Research Centre of Earthquake Surveying,X iam en 361021 3)Faculty of Science,Kobe University,Rokkotaim achi1-1,N ada,Kobe6578501,Japan)
On the basis of deducing the universal expressions in an orthogonal curvilinear coordinate system of the displacement gradientmatrix and the strain tensormatrix of displacement vectors,we further derive the universal expression of the conversional matrix between two partial coodinates in random different orthogonal curvilinear coordinate systems,meanwhile,indicats that this conversionalmatrix also belongs to the orthogonalmatrixes so that the strain tensormatrixes are similarmatrixes.W ith this understanding,the after deply analysisof the geometric and physical natures of the strain tensormatrixes,discovers the invariant code mystery of crustal deformation hidden in these matrixes,which is,whatever the orthogonal curvilinear coordinate system is,the strain tensormatrix has a unique and invariant principle strain characteristic polynomial and by its corresponding strain eigenvalue equation we can derive the principle strainswith their directions at any crustal particle,then the matrix can be turned into a diagonalmatrix by putting the principle strains values as its diagonal elements,and the matrix trace equals the body strain,the matrix determinant equals a product of the principe strains.All these geometric and physical quantities are the crustal deformation invariants at the spot.
displacement gradient matrix;strain and rotation tensor matrix;universial expression;geometric and physical invariant;opting for a coordinate system
(1)福建省地震局,福州 350003 2)厦门地震勘察研究中心,厦门 361000 3)日本神戸大学大学院理学研究科,神戸 6578501)
1671-5942(2011)04-0066-05
2011-01-26
中国地震局老专家科研基金
刘序俨,男,研究员,长期从事固体潮与地壳形变研究.E-mail:xuyanliu@126.com
O347
A
