多偏差变元的捕食-被捕食Lotka-Volterra模型的周期正解

徐 燕，鲁世平

(安徽师范大学数学与计算机科学学院,安徽 芜湖 241000)

多偏差变元的捕食-被捕食Lotka-Volterra模型的周期正解

徐 燕，鲁世平*

(安徽师范大学数学与计算机科学学院,安徽 芜湖 241000)

作者研究了一类多偏差变元3种群捕食-被捕食Lotka-Volterra模型.通过利用重合度拓展定理和一些分析技巧,得到了该模型的周期正解的存在性.

周期正解;重合度拓展定理;Lotka-Volterra捕食-被捕食种群模型

1 引言及预备

近年来,许多人将泛函微分方程理论应用到生态数学当中,并且提出了各种各样的模型，如在人口力学、生态学和流行病学等方面,尤其是人口力学Lotka-Volterra模型,由于在理论和实践方面的重要性,已被越来越广泛地应用.吕翔用Krasnoselskii固定点定理获得了模型[1]

(1)

的周期正解的存在性.其中x1(t)表示在时刻t被捕食动物的数量,x2(t)和x3(t)表示在时刻t捕食动物的数量,ri,aij∈C(R,[0,∞))和τij∈C(R,R)都是w-周期函数且

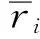
近年来,许多作者运用重合度理论解决周期解存在问题,如鲁世平证明了一类多偏差变元的n种群Lotka-Volterra模型的周期正解[2].范猛,王克研究了具有偏差变元的捕食者-食饵系统全局周期解的存在性[3].受此启发,该文利用重合度理论得出模型(1)周期正解的存在性.

2 主要引理

引理1[2]如果τ∈C(ω)满足τ∈C1(R,R)且τ′(t)<1,∀t∈[0,ω],则函数t-τ(t)存在唯一反函数μ(t)满足μ∈C(R,R)且μ(a+ω)=μ(a)+ω,∀a∈R.

注1如果g∈C(ω),τ∈C(ω)满足τ∈C1(R,R)且τ′(t)<1,∀t∈[0,ω],由引理1易见g(μ(t+ω))=g(μ(t)+ω)=g(μ(t)),∀t∈R,其中μ(t)∈C(R,R)为t-τ(t)的反函数,故g(μ(t))∈C(ω).

(a) ∀x∈∂Ω∩D(L),λ∈(0,1),Lx≠λNx;

(b) ∀x∈∂Ω∩KerL,QNx≠0;

为了利用引理1和引理2,文中设X=Y=C(ω):={x|x∈C(R,R3),x(t+ω)≡x(t)},ω>0为常数,其模定义为‖x‖=maxt∈[0,ω]|x(t)|,再设τij′<1,由此得函数t-τ(t)存在连续反函数,记为σij(t),i,j=1,2,3.

注2利用引理1，不难发现σij(ω)=σij(0)+ω,i,j=1,2,3.

作变换xi(t)=expyi(t),(i=1,2,3),则系统(1)可化为

(2)

显然系统(1)存在ω-周期正解当且仅当系统(2)存在ω-周期解.

3 主要结果

设

(3)

其中D(L)={y|y∈X,y(t)∈C(R,R3)},N:X→Y,

(4)

定理1设下面条件满足：

[Ⅱ] 系数矩阵detA>0且detAi>0,矩阵A和Ai(i=1,2,3)由式(10)(11)所定义,则系统(1)存在ω-周期解.

证设y(t)为系统Ly=λNy,λ∈(0,1)的任一ω-周期解,其中L,N分别由式(3)(4)所定义,则

(5)

将式(5)两端同在[0,ω]上积分,得

(6)

(7)

将式(7)代人(6),同时记

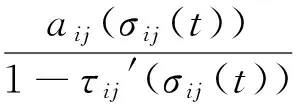
(7′)

(8)

由广义积分中值定理知,存在ξij∈[-τij(0),ω-τij(0)],使得

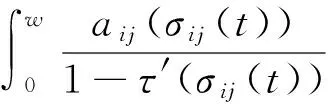
其中ηij=σij(ξij)∈[0,ω].

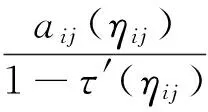
(9)

令A=(Λ1,Λ2,Λ3)为式(9)的系数矩阵,其中

Λ1=(a11,a21,a31)T,Λ2=(a12,-a22,-a32)T,Λ3=(a13,-a23,-a33)T.

(10)

同时取

2.2 两组新生儿指标比较 观察组新生儿出生体质量、巨大儿4例(5.00%)，对照组分别为(3.81±0.73)kg和15例(18.75%)，差异有统计学意义(t=-8.33，P=0.02；χ2=21.60，P=0.00)；两组新生儿窒息率均为2.50%(2/80)，差异无统计学意义(χ2=1.31，P=1.24)。

(11)

|yi(ti)|≤Ri,i=1,2,3.

(12)

再由式(5),得

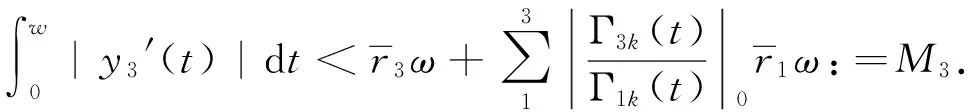
由此并结合式(12),得

|yi|0≤Ri+Mi,i=1,2,3.

(13)

进而有

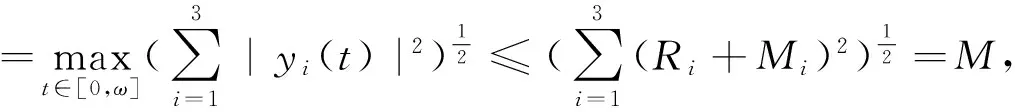
显然M<∞为与λ无关的常数.如果y∈KerL,则y为R3中的常向量.故由注2知

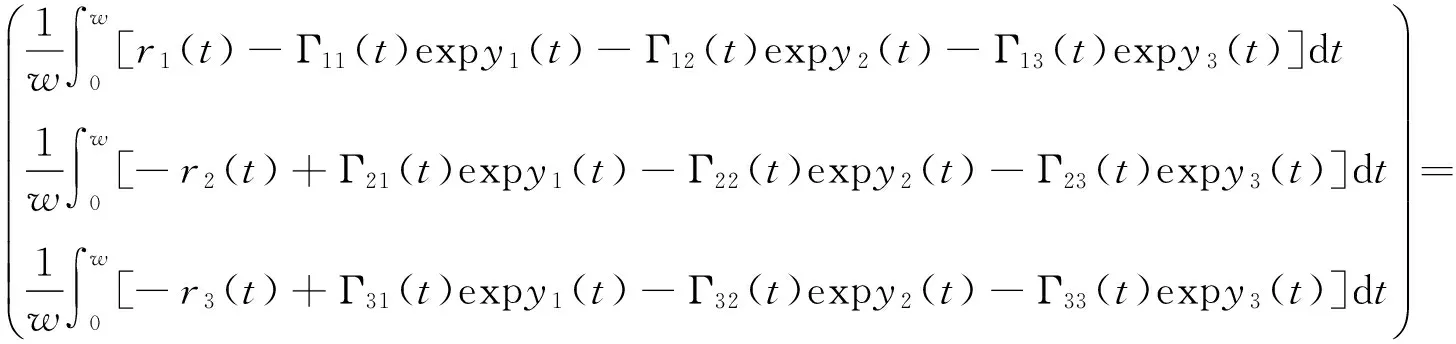
(14)

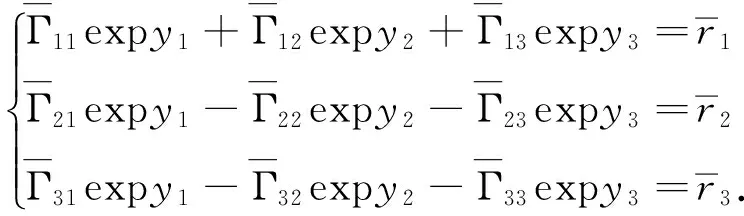
(15)

[1] Lü Xiang, Lu Shiping, Yan Ping. Existence and global attractivity of positive periodic solutions of Lotka-Volterra predator-prey systems with deviating arguments[J]. Nonlinear Analysis:Real World Applications,2010,11:574-583.

[2] 鲁世平.一类多偏差变元的n种群Lotka-Volterra模型的周期正解[J].数学学报,2005,48(3):427-438.

[3] 范猛,王克.具偏差变元的捕食者-食饵系统全局周期解的存在性[J].应用数学学报,2000,23(4):557-561.

[4] Gaines R E, Mawhin J L. Coincidence degree and nonlinear differential equations[M]. Berlin:Springer-Verlag,1977.

PositivePeriodicSolutionsofLotka-VolterraPredator-PreySystemswithMulti-DeviatingArguments

XU Yan, LU Shi-ping

(College of Mathematics and Computer Science, Anhui Normal University, Wuhu 241000, China)

This paper studied on a class of 3-species Lotka-Volterra predator-prey system with multi-deviation arguments and obtained the existence of positive periodic solutions for this model by continuation theorem and some analysis techniques.

positive periodic solutions; coincidence degree theory; Lotka-Volterra predator-prey system

10.3969/j.issn.1674-232X.2011.02.009

2010-09-03

徐 燕(1985—),女,安徽安庆人,应用数学专业硕士研究生,主要从事泛函微分方程研究.

*通信作者：鲁世平(1962—),男,安徽无为人,教授,主要从事泛函微分方程研究.E-mail: lushiping26@sohu.com

O175.1MSC201034K13;34K40

A

1674-232X(2011)02-0133-04