FCR-代数在Cleft扩张下的不变性

张棉棉

(杭州师范大学理学院，浙江 杭州 310036)

FCR-代数在Cleft扩张下的不变性

张棉棉

(杭州师范大学理学院，浙江 杭州 310036)

文章主要讨论FCR-代数在半单Hopf代数Cleft扩张下的不变性.文中首先给出Cleft扩张和交叉积之间的联系.然后证明了:当H是有限维半单余半单Hopf代数时,FCR-代数在H-Cleft扩张下是不变的.

Cleft扩张；交叉积；FCR-代数

0 引 言

FCR-代数是一类非常有趣的代数.其概念的产生源自特征为0的半单李代数g的包络代数U(g)广为人知的性质(见文献[1]):

1) U(g)的每个有限维表示是完全可约的;

2) U(g)是residually有限维的,即U(g)的所有有限维表示的核的交为{0}.

1994年,Kraft和Small在文献[2]中把满足上述两个性质的代数定义为FCR-代数.具体地,称一个代数R为FCR-代数,如果R的每个有限维数表示是完全可约的,且R是residually有限维的.

经典的FCR-代数例子有:有限维半单代数,半单李代数的包络代数(特征为0的情况),量子包络代数Uq(g)(q不是单位根),以及orthosymplectic李超代数osp(1,2r)的包络代数U(osp(1,2r))[3].

文献[2]的命题1证明了:如果R是一个域k上Noetherian的FCR-代数,G是R的一个有限自同构群,且k的特征与G的阶数互素,那么不变子环A=RG也是一个FCR-代数.

文献[3]的命题2.2证明了:设S是R的正规扩张,且S作为R-模是忠实平坦的.如果S是一个FCR-代数,那么R是一个FCR-代数.

文献[4]的定理5.4证明了:设H是一个有限维半单Hopf代数,R是一个H-模代数.如果R是一个FCR-代数,那么A=R#H是一个FCR-代数.

在此主要考虑FCR-代数在半单Hopf代数Cleft扩张下的不变性.

1 准备知识

文章假定k是域,涉及到的代数为k-代数,如无特别指出,涉及到的模为左模.

设B是一个k-代数,A是B的一个子代数,H是一个Hopf代数.则有如下定义:

1) 称A⊂B为(右)H-扩张,如果B是一个右H-余模，ρ是余模映射，BcoH={b∈B:ρ(b)=b⊗1}是B的子余模,则BcoH=A.

2) 称一个H-扩张A⊂B为H-Cleft,如果存在一个(卷积)可逆的右H-余模映射γ:H→B.

3) 称一个H-扩张A⊂B为右H-Galois,如果映射β:B⊗AB→B⊗kH是双射,其中β(a⊗b)=(a⊗1)ρ(b).

4) 一个H-扩张A⊂B被称为存在(右)normal basis property,如果B≅A⊗H作为左A-模和右H-余模.

Doi和Takeuchi在[5]对具有normal basis property的Galois扩张进行了刻划，见如下定理.

定理1[5]设A⊂B是H-扩张.下列条件是等价的:

1)A⊂B是H-Cleft.

2)A⊂B是H-Galois,存在normal basis property.

从上面这个结论,知道Cleft扩张不但是Galois扩张的一个特殊情况,而且推广了群的Galois理论的经典定理:如果F⊂E是域上的有限Galois扩张,G是Galois群，则E/F存在normal basis.因此,Cleft扩张在Hopf代数的Galois理论中显得很重要.

假设H度量A,σ∈Hom(H⊗H,A)是一个卷积可逆映射.则A与H的交叉积A#σH是线性空间A⊗H配上乘法

(a#h)(b#k)=∑a(h1·b)σ(h2,k1)#h3k2

其中a,b∈A,h,k∈H.这里把a⊗h记作a#h.

定理2[5-6]交叉积A#σH是一个单位元为1#1的结合代数当且仅当满足下面2个条件:

1)A是一个模作用为·的twistedH-模.即对任意的h,k∈H,a∈A,满足

1·a=a,h·(k·a)=∑σ(h1,k1)(h2k2·a)σ-1(h3,k3),

2)σ是一个cocycle.即对任意的h,k,m∈H,满足

σ(h,1)=σ(1,h)=ε(h)1,∑(h1·σ(k1,m1))σ(h2,k2m2)=∑σ(h1,k1)σ(h2k2,m).

对任意的a∈A,h∈H,显然有(a#1)(1#h)=a#h.从而可以得到A≅A#σ1和H≅1#σH.因此A和H可以被看作是A#σH的子代数.一般把(a#1)和(1#h)简单记为a和h.于是有ah=a#h等.特别地,A#H是交叉积的特殊情形.

下面给出H-Cleft与交叉积之间的联系.

定理3[4]H-扩张A⊂B是一个H-Cleft,且存在一个右卷积可逆H-余模映射γ:H→B当且仅当B≅A#σH是一个代数,σ:H⊗H→A是一个卷积可逆映射,其中h·a=∑(h)γ(h′)aγ-1(h″)给出了A作为twistedH-模结构的作用.

2 FCR-代数

引理1设H是一个有限维Hopf代数,A是一个twistedH-模代数,σ∈Hom(H⊗H,A)是一个cocyle,R=A#σH是一个交叉积代数,则有:

1) 如果H是半单的,A的每个有限维同态像是半单的,那么R的每个有限维同态像是半单的.

2) 如果H是余半单的,R的每个有限维同态像是半单的,那么A的每个有限维同态像是半单的.

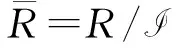
2) 可直接由1)和对偶定理([4],推论9.4.17)得到.具体地,根据对偶定理(A#σH)#H*≅Mn(A),R=A#σH的每个有限维同态像是半单的,余半单Hopf代数H的对偶Hopf代数H*是半单的,以及Smash积是特殊的交叉积这些性质,直接由1)即可推出R#H*的每个有限维同态像是半单的.再利用对偶定理,可知A的每个有限维同态像是半单的.

引理2设H是一个有限维Hopf代数,A是一个twistedH-模代数,σ∈Hom(H⊗H,A)是一个cocyle,R=A#σH是交叉积代数.则有R是residually有限维当且仅当A是residually有限维的.

证明因为性质residually有限维是在子环意义下保持不变的,所以由R=A#σH是residually有限维的,直接得出A是residually有限维的.反之,A是residually有限维的,那么Mn(A)是residually有限维的,再根据对偶定理R#H*=(A#σH)#H*≅Mn(A),得R是residually有限维的.

引理3设R是一个代数,以下两条是等价的:

1)A的每个有限维表示是完全可约的,

2)A的每个有限维同态像是半单的.

证明1)⟹2)设B=A/I是A的一个有限维同态像,V是任一有限生成左B-模,那么显然V是A的有限维表示.于是V是完全可约的.因此,B是半单的.

2)⟹1)设V是A的一个有限维表示,那么V是有限维同态像A/annAV的一个表示,其中annA(V)={a∈A|aV={0}},所以V是完全可约的.

定理4设H是一个有限维半单余半单Hopf代数,A是一个twistedH-模代数,σ∈Hom(H⊗H,A)是一个cocyle,R=A#σH是交叉积代数.则A是一个FCR-代数当且仅当R=A#σH是一个FCR-代数.

证明直接由引理1,引理2,引理3得到.

[1] Dixmier J. Enveloping algebras[M]. Amsterdam: North-Holland Publishing Company,1977.

[2] Karft H P, Small L W. Invariant algebras and completely reducible representations[J]. Math Research Letters,1994(1):297-307.

[3] Kirkman E, Small L W. Examples of FCR-algebras[J]. Comm. Algebra,2002,30(7):3311-3326.

[4] Montagomery S. Hopf algebras and their actions on rings[C]//CBMS Lecture Notes 82, Providence, RI: Amer Math Soc,1993.

[5] Doi Y, Takeuchi M. Cleft comodule algebras and Generic Modules[J]. Comm Algebra,1986,14:801-818.

[6] Blattner R J, Cohen M, Montgomery S. Crossed products and inner actions of hopf algeras[J]. Trans AMS,1986,298:671-711.

[7] 张寿传.交叉积的同调维数[J].数学年刊,2001,22A(6):767-772.

InvariantPropertiesofFCR-AlgebrasunderCleftExtension

ZHANG Mian-mian

(College of Science, Hangzhou Normal University, Hangzhou 310036, China)

The paper discussed the invariant property of FCR-algebra under Cleft extension of a semisimple Hopf algebra provided the relations between the Cleft extension and the crossed product and proved that when the finite dimensional Hopf algebraHis semisimple and cosemisimple, FCR-algebra is invariant under theH-Cleft extension.

Cleft extension; crossed product; FCR-algebra

10.3969/j.issn.1674-232X.2011.02.003

2010-07-19

数学天元基金项目(11026207)；浙江省自然科学基金项目(Y6100173)；杭州师范大学科研启动基金项目(HSKQ0015).

张棉棉(1980—),女,浙江慈溪人,讲师,博士,主要从事代数研究.E-mail: zhmm1216@yahoo.com.cn

O153MSC201016G10

A

1674-232X(2011)02-0106-03