基于线性方程组的秘密共享方案

沈忠华，于秀源

(杭州师范大学理学院，浙江 杭州 310036)

基于线性方程组的秘密共享方案

沈忠华，于秀源

(杭州师范大学理学院，浙江 杭州 310036)

在门限方案中，密钥被所有成员秘密共享，而当一定数量的成员合作时，该密钥可以恢复.一个(t,n)门限方案就是将密钥K分给n个成员，而任意t个成员合作可以生成密钥K，但只有t-1个成员或者更少的成员不能生成该密钥.大多数(t,n)门限方案都基于Lagrange插值多项式或者是同余理论.文章提出了一种新的基于多元一次多项式的秘密共享门限方案.

密码学；秘密共享；线性方程组

0 引 言

存储在系统中的所有密钥的安全性可能最终取决于一个主密钥.这样做有两个缺陷：一是若主密钥偶然地或蓄意地暴露，整个系统就易受到攻击；二是若主密钥丢失或毁坏，系统中的所有信息就用不成了.后一个问题可通过将密钥的副本发给信得过的用户来解决.但这样做时，系统对背叛行为又无法对付.解决这两个问题的一个办法就是使用秘密共享方案(secret sharing scheme)[1].秘密共享方案是与密钥建立相关的多方协议.它通过利用n个用户中的t个用户之间的相互协作，从而控制某些重要任务，并为这些重要任务的可信分发或共享控制提供便利.秘密共享的思想开始于将一个秘密分成若干份，每一份称为一个共享，这些共享被分发给不同的用户，只有用户特定子集的共享共同提供才能重构初始秘密.

用数学的语言，秘密共享方案的基本思想如下：将密钥k按下述方式分成n个共享(share)k1,k2,…,km:

1) 已知任意t个ki值易于算出k；

2) 已知任意t-1个或者更少个ki，则由于信息短缺而不能决定出k.这种方法也称为(t,n)门限(threshold)法[2].

将n个共享k1,k2,…,kn分给t个用户.由于重构密钥要求至少有t个共享，故暴露t1(t1≤t-1)个共享不会危及密钥，且少于t个用户的组不可能合谋得到密钥.同时，若一个共享被丢失或毁坏，仍可恢复密钥(只要至少有t个有效的共享).

对于秘密共享方案，很多文献已有了较好的阐述，但大多都基于Lagrange插值多项式的Shamir方案[1]和基于同余理论的Asmuth-Bloom方案[3-4].1983年Karnin-Greene-Hellman在文[7]中提出了基于矩阵乘法的秘密共享方案,在此对Karnin-Greene-Hellman秘密共享方案作进一步改进,提出一种新的基于线性多项式的门限方案,在方案中借助数论中的同余理论,使得安全性得到加强,另外在密钥的选取上较之Karnin-Greene-Hellman方案更加简单.

1 门限函数

众所周知，一个门限方案必须满足这样的条件：如果将一个信息E分成n个子信息，那么，对于给定的t，由t个子信息可以完整地得到E，而由任何少于t个的子信息却不能完整地得到E.

把门限方案看作一个函数，那么，门限方案的设计就是寻求满足下述条件MXT的k元函数y=f(X)，X=(x1,x2,…,xk)∈Rk：

显然，采用满足条件MXT的函数y=f(x1,x2,…,xk)设计秘密共享门限方案时，信息E可以是这个函数的某个既定的函数值，例如，f(0,0,…,0)，f(1,1,…,1).

定义1满足条件MXT的函数称为门限函数.

定义2设B=(bi,j)1≤i,j≤t和C=(ci,j)1≤i,j≤t是两个整数矩阵，

bi,j≡ci,j(modm),1≤i,j≤t，

则称B和C关于modm同余，记为B=C(modm).

根据定义1，以下规定，在矩阵中出现的整数都是关于modm的最小非负剩余.

记B=|B|，C=|C|，则当B≡C(modm)时，显然有B=C(modm).

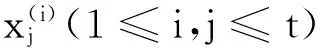
定理1设X是整数矩阵，X=|X|，(X，m)=1，则方程组

(1)

有唯一解(a1,…,at)(modm).

证明方程组(1)等价于方程组

(2)

其中(δ1,δ2,…,δt)∈Rt.

由于(X，m)=1，所以X=|X|≠0，因此，存在X的逆矩阵X-1，使得XX-1=E，此处E是单位矩阵.于是，

A=X-1Yt

(3)

由此及利用克莱姆规则[4]可得，对于固定的Yt，式(3)是唯一.

此时设X的伴随矩阵为X*，则由[4]可知XX-1=X*，又(X，m)=1，所以

X-1≡X-1X*(modm)

(4)

这里X-1为X的模m逆元，满足X-1X≡1(modm).

因此由(3)及(4)可得：A≡X-1X*Y(modm).定理结论成立.

推论函数y=a1x1+…+atxt是门限函数.

证明设有t个人分别掌握(y(i),X(i))，其中

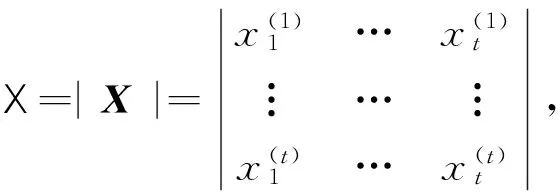
(5)

有唯一解(a1,…,at)(modm).

2 基于线性方程组的(t,n)秘密共享门限方案

2.1 参数的选定

1) 可信中心选取大整数m；

2) 可信中心选取n×t矩阵

使得它的任何一个t×t子阵的行列式的值与m互素；

2.2 门限函数的设定

选取函数y=f(x1,x2,…,xt)=a1x1+…+atxt∈Zp[x1,x2,…,xt]，则由推论可知其为门限函数.假定共享的密钥为k∈Zm，并约定k=f(1,1,…,1).

2.3 个人密钥的设定

1) 对于每个共享者Pi(1≤i≤n)，可信中心计算

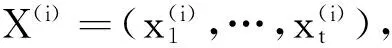
2.4 对矩阵X选取的说明

要选取X，一般来说，需要计算它的所有t×t子阵的行列式以保证它们都与m互素.当t和m较大时，需要较多的计算.因此，在选取矩阵X时，应该注意这些行列式的计算.例如，可以是如下n×t(n>t,t>2)阶矩阵：

(6)

因该矩阵任一t×t子阵的行列式是比较容易计算的.事实上，设矩阵X的一个t×t子阵为Xi，

则其行列式值的计算可利用范德蒙行列式[5]的结果，即，

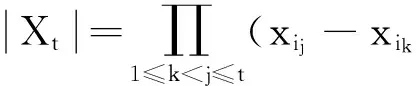
(7)

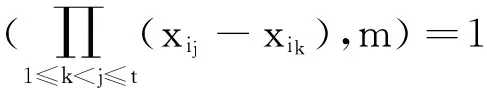
2.5 共享密钥的恢复

n个共享者只要有t个人合作就可以将密钥恢复，不失一般性，假设有P1,P2,…Pt参与恢复密钥，则只需他们每人贡献(y(i),X(i))(1≤i≤t)，由定理1，通过方程

可计算出(a1,…,at)(modm)，且该解是唯一的.从而可以通过y=f(x1,x2,…,xt)=a1x1+…+atxt恢复密钥k=f(1,1,…,1).

如若合作成员为t1(t1

无法得出唯一解(a1,…,at)(modm)，因此不能得出正确的共享密钥.

2.6 一个例子

假定要构建一个基于多元一次多项式的(3,5)秘密共享门限方案，则做如下工作

1) 选定素数p=47；

2) 选取5×3阶矩阵

显然它们都与p=47互素.

3) 选定门限函数y=f(x1,x2,x3)=x1+2x2+x3，需保密.约定共享的密钥为k=f(1,1,1)=4；

5) 共享密钥的恢复

假定这5个共享成员中有3人合作，不妨设作P1,P2,P4，则他们可通过方程

计算出a1=1,a2=2,a3=1.从而可得知k=f(1,1,1)=4.

3 结 论

大多数(t,n)门限方案都基于Lagrange插值多项式或者是同余理论.该文中对Karnin-Greene-Hellman秘密共享方案作了进一步改进,提出一种新的基于线性多项式的门限方案,不同于Karnin-Greene-Hellman秘密共享方案中简单的矩阵运算,笔者借助了数论中的同余理论,使得方案的安全性得到加强.另外对于密钥的选择和计算上,该方案较之Karnin-Greene-Hellman方案更加简单.该方案具有在决定共享密钥时有更多的选择、计算时更简单(因为是线性方程组，所以无须像插值多项式一样算n次幂)等方面的优势，因此更具有普遍意义.

[1] Shamir A. How to Share a Secret[J]. Comm. ACM,1979,22(11):612-613.

[2] Desmedt Y, Frankel Y. Threshold cryptosystems[C]//Advances in Cryptology-Crypto-89, London: Springer Verlag,1998:307-315.

[3] Yacobi Y. Efficient Electronic Money[C]//Advances in Cryptology-ASIACRYPT’94. London: Springer-Verlag,1994:153-163.

[4] 于秀源,薛昭雄.密码学与数论基础[M].济南：山东科学技术出版社,1993.

[5] Thomas W. Hungerford, Algebra[M]. London: Springer-Verlag,1974:354-354.

[6] Kennetn Hoffman, Ray Kunze. Linear Algebra[M]. New Jersey: Prentice Hall, Inc. Englewood Cliffs,1971:124-125.

[7] Ehud D K, Jonathan W G, Martin E H. On Secret Sharing Systems[J]. IEEE Transactions on Information Theory,1983，29:35-41.

ASecretShareThresholdSchemeBasedonMultivariateLinearPolynomial

SHEN Zhong-hua, YU Xiu-yuan

(College of Science, Hangzhou Normal University, Hangzhou 310036, China)

In a threshold scheme, a secret key is shared among a group of people in such a manner that a certain number of them can work together to recover the secret. A (t,n) threshold scheme is a scheme to distribute the secret keyKintonusers in such a way that anytusers can cooperate to reconstructKbut a collusion oft-1 or less users reveal nothing about the secret key. Most (t,n) threshold schemes all base on Lagrange interpolation or Chinese Remainder Theorem. This paper proposed a new threshold scheme based on multivariate linear polynomial.

cryptograph; secret share; multivariate linear polynomial

10.3969/j.issn.1674-232X.2011.02.002

2010-09-18

国家自然科学基金项目(10671051)；国家自然科学基金项目(61070153);浙江省教育厅科研项目(Y201016497)；杭州市高校重点实验室科技创新项目(20100331T11);杭州师范大学科研项目(2010QN26).

沈忠华(1973—)，男，浙江杭州人，副教授，主要从事数论及其应用、密码学和信息安全技术等研究.E-mail: ahtshen@126.com

TP309;O153MSC201011T71;94A60

A

1674-232X(2011)02-0101-05