基于ADAMS的FSAE赛车转向梯形机构的优化设计

廖小亮，孙泽海

（西华大学 交通与汽车工程学院，四川 成都610039）

转向机构对于汽车的转向性能、操纵稳定性、舒适性和汽车轮胎使用寿命等有着很大的影响，其设计的主要任务就是保证汽车转向过程中所有车轮均绕同一瞬时转向中心转动，以避免或减少车轮侧滑，这在赛车设计上尤为重要［1－4］。目前已有不少人在转向机构的优化设计方面做过研究［5－6］。ADAMS是一个功能强大的MCAE软件，已广泛应用于机械系统的仿真分析［7］，为了提高FSAE赛车的转向性能，本文利用ADAMS软件建立了FSAE赛车的虚拟样机悬架和转向系统模型，分析了转向机构关键点对阿克曼转向特性的影响。建立多个设计变量以及相应的约束条件，并建立目标函数，对转向系进行多变量优化。

1 建立参数化前悬转向模型

1.1 初始模型的建立

根据赛车要求，初步选择初始参数：转向梯形机构上有梯形臂长L1为72，底角γ0为73°，齿条和横拉杆交点位置坐标（X=－115，Y=0，Z=190）。 加上初始车轮前悬定位参数如主销的内倾、主销后倾、车轮外倾和车轮的前束参数，再根据赛车的各个构件设计时的具体三维坐标参数，建立赛车悬架转向机构的虚拟样机模型如图1～2所示。

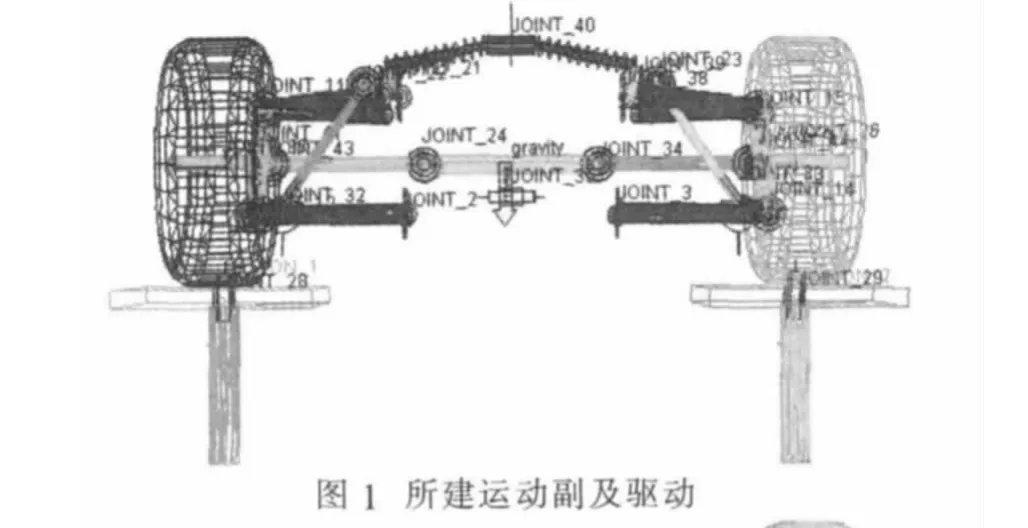
1.2 设计变量及约束条件的建立

1.2.1 设计变量建立

由给定的汽车初始参数，将转向梯形机构上的梯形臂长L1，底角γ，齿条和转向横拉杆的交点位置坐标（X，Y，Z）建立为5个设计变量。其中X轴正方向为汽车的前进方向，Y为重力加速度方向。对于底角γ选一个初始值γ0，再增加或减小角度进行优化搜索。Z坐标反映的是转向器齿条长度，根据实际情况选择优化搜索范围为170～210mm。Y坐标反映转向器的安装高度，根据条件选择优化范围为－20～20mm。对于L1及转向器距前轴距离X的取值范围则结合约束条件确定。

1.2.2 约束条件确定

首先梯形臂在前轴中心水平面上，要保证梯形臂不与车轮上的零部件发生干涉，必须满足：

式中：ALx为梯形臂球头中心X坐标值，即－L1sinγ；ACX为车轮上可能与梯形臂干涉的X坐标值。所以可以选定L1上限为

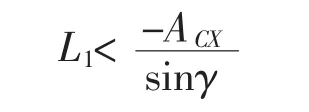
根据传力要求，梯形臂也不能过短，故取L1的下限为65mm。

其次，转向器的安装距离h（即－X）对传动角α的影响较大，为了保证良好的传动角α，在此次设计中约束齿条与横拉杆夹角ξmax不大于150°，由此可建立以下关系式：

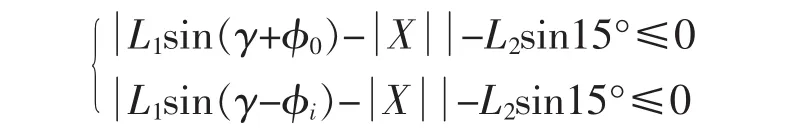
式中：φ0，φi分别为外内梯形臂与前轴夹角的变化量；L2为横拉杆长度。

由于在 φ0、φi的全部取值范围内，sin（γ+φ0）的最大值为 1，sin（γ－φi）的最小值为 sin（γ－φimax），所以X的取值范围为

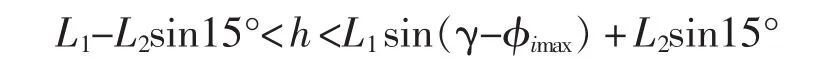
同时横拉杆与梯形臂的夹角也会影响传动角，随着车轮转角增大，传动角减小。对应的同一齿条行程，内轮的传动角αi总比外轮一侧传动角α0要小。

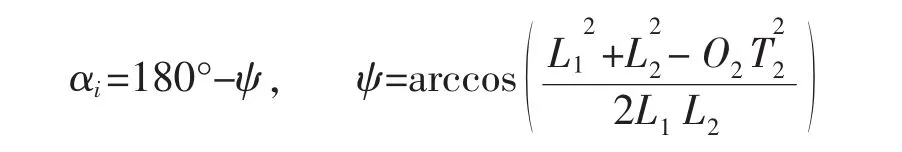
式中：ψ为梯形臂与横拉杆的夹角；O2T2为梯形臂与主销的交点到同侧齿条端点的距离。为了保证有一定的传动角，所以αimin不小于40°。

最后约束齿条行程S，由于选定了转向器，得到了符合此转向器的齿条行程范围（20.2，26）mm。

2 优化目标函数的建立

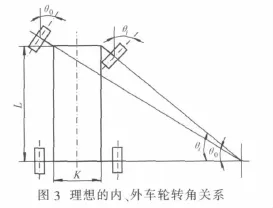
2.1 理想梯形结构

如图3所示，为了使汽车转向时各轮胎只作滚动而无滑动，根据阿克曼(Ackerman)理论转向特性得到的右轮转角期望值为［8］

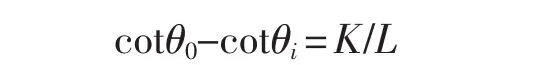
式中： θ0为外轮转角（°）；θi为内轮理论转角（°）；K为两主销中心距（mm）［15］，L 为轴距（mm）。 由此可知，在给定的外轮转角下的理想内轮转角：

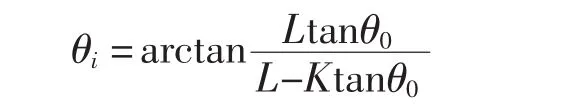
2.2 优化目标函数的建立

转向梯形机构的优化目标就是要在规定的外轮（或内轮）转角范围内，实际的内轮（或外轮）转角尽量的接近理论的内轮（或外轮）转角。所以建立目标函数如下：

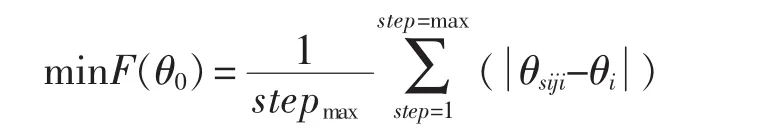
由于赛车的比赛场在上海国际卡丁车赛车场，弯道数量比较密集，且弯道又急，驾驶员需频繁转向，因此转向梯形的优化转角范围非常重要。根据经验可知，赛车外转向轮将会频繁的在0°～20°之间变换行驶。因此为了在行驶过程中汽车有良好的转向性能、驾驶舒适性和较高轮胎寿命等，确定优化的目标转角范围为 0°～20°。

由于要达到最小转弯半径4.5 m要求，所以外轮变化范围为0°～22°，但根据赛场实际要求优化0°～20°，其实现函数如下：

IF （.XHU_FSAE.Angle_left－20*pi/180:ABS（.XHU_FSAE.Siji_neilun － .XHU_FSAE.lilun_neilun），0，0） +5/20*IF （.XHU_FSAE.Angle_left－20*pi/180:ABS（.XHU_FSAE.Siji_neilun－.XHU_FSAE.lilun_neilun)，0，0）

3 优化结果及分析

3.1 优化方法和过程

通过所建立的参数化模型，建立了5个优化变量。由于设计时根据使用要求（转弯半径要求等），转向机构设计时选定了初始值，然后根据赛车的实际情况如转向机构安装位置的限制，转向器的选型的限制等，对变量优化范围进行了限制，各个变量限制在一定范围内。在ADAMS中利用带变量的表达式将梯形臂长、转向横拉杆的交点位置和底角，以及相关约束副的位置和方向作相应的参数化，并建立相应的测量函数，优化目标和约束条件，运行ADAMS自带优化程序进行计算［7］。

3.2 初步优化结果分析

首先考虑到转向器的已确定，所以将转向横拉杆的交点的Z轴作为定值进行优化，由ADAMS优化后所获得变量值的最终结果如表1所示。从表1可以看出，进行初步优化过后的转角平均误差由0.17473降为0.047824，理论转角与实际转角的重合度得到提高。由ADAMS初步优化后，理论内轮转角及实际内轮转角随外轮转角的变化曲线如图4所示，其理论与实际内轮转角误差如图5所示。

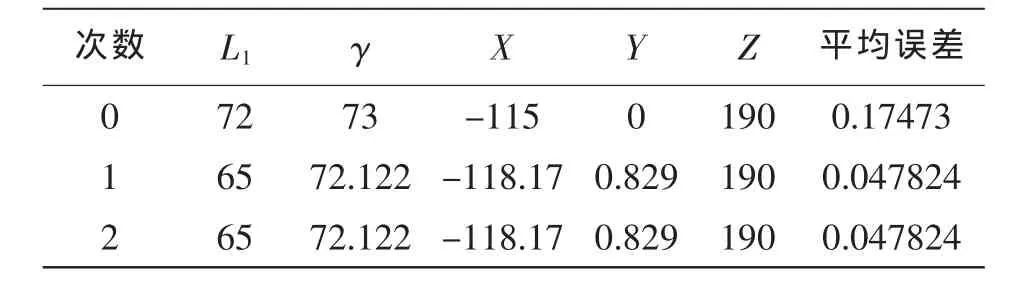
表1 初步优化结果

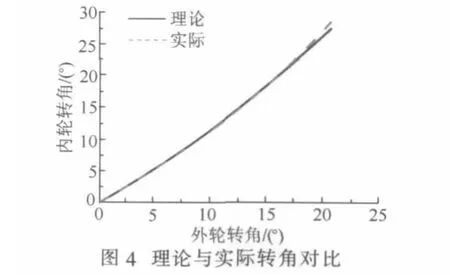
由图 4～5 可知，外轮转角 θ0在 0°～22°的转动范围内，起初实际内轮转角小于理论内轮转角，随着θ0不断增大，理论转角和实际转角的误差不断增大，并在11.8°得到峰值0.0979°。过后逐渐减少，在15.8°两曲线相交，误差为0。此后随着增大，实际内轮转角大于理论内轮转角，误差不断加大，在22°取得最大误差为 1.144°。

3.3 最终优化结果分析

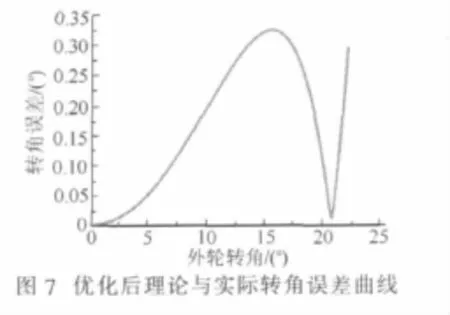
在初步优化的基础上继续进行优化，并将转向横拉杆的交点的Y和Z都作为变量进行优化，由ADAMS优化所获得的最终优化结果如图6～7所示，由图可知，经过再次优化后，实际内轮转角随外轮转角的变化和理论内轮转角随外轮转角变化基本一致，误差较小，在外轮转角为15.5°时出现最大误差，其值值为0.309°。由此可知，优化后内外车轮转向角的变化曲线更加接近理想阿克曼转角曲线，使得赛车的转向性能得到了提高。

由ADAMS最终优化所获得的梯形机构的最终参数： γ 为 72.99°；L1为 65.88 mm；X 为 113.68；Y 为0.814；Z为 189.74；S 为 24.04mm；L2为 327.6mm。由优化后参数可知Z值的变化很小，这时不需对转向器齿条进行修改。

4 结论

采用多体动力学软件ADAMS对转向梯形机构进行了优化设计，最终的优化结果表明，通过优化使得赛车的转向更加接近理想转向特性，赛车的转向性能得到了提高，获得了比较满意的结果。同时也表明了运用ADAMS软件可以方便、精确地对机械系统进行建模和优化设计，减少了繁琐的数学公式的推导。

此次优化采用的是以梯形臂、梯形底角在前轴中心水平面上，以梯形臂长度、梯形臂底角、转向器前后安装距离及转向器上下安装位置为变量。其中限制转向器上下安装位置在较小的变化范围，保证对传动角的影响尽量小。在此优化过程中，发现转向器上下安装位置的变化，对优化结果影响不大，在以后优化过程中，可考虑转向器安装位置与梯形臂置于同一水平上。

［1］周兵，杨凡，徐琪.基于ADAMS的转向机构的优化设计［J］.湖南大学学报，2008,35（12）:23－26.

［2］ 韦超毅，蒋国平，周从矩，等.基于ADAMS软件的转向梯形计算机辅助设计［J］.广西大学学报，2003,28（3）：246－248.

［3］ 向铁明，任恒山，朱易铭.赛车转向梯形优化设计方法［J］.厦门理工学院学报，2009,17（4）：48－50.

［4］ 王敏，赵京，陶民华，等.汽车转向机构的优化设计［J］.汽车工程，1995,17（6）：360－366.

［5］ 初亮，高义民，王志浩，等.滑柱臂式悬架断开点位置的优化及分析［J］.汽车工程，1996,18（6）：365－369.

［6］蒋国平，王国林，周孔亢.独立悬架转向梯形断开点位置的优化设计［J］.农业机械学报，2007，38(2)：30－34.

［7］ 李军，邢俊文，覃文洁，等.ADAMS实例教程［M］.北京理工大学出版社，2002:1－25.

［8］ 陈家瑞.汽车构造［M］.北京：人民交通出版社，2005：263－268.