基于ANOVA法磨削过程统计控制研究
2011-11-22王维志
王维志
(湖北汽车工业学院 机械工程系,湖北 十堰442002)
在机械加工制造领域,人们一直用过程能力指数Cpk评价生产过程满足产品技术规格要求的能力[1-2]。 这里提出一个问题,Cpk评价的是不是生产过程持续满足产品技术规格要求的能力,结论显然是否定的。只有当生产过程是稳定的,或者说是始终处于统计稳态,结论才是肯定的,而Cpk本身并不能保证这一点。因此,需要另外一种方法,计算Cpk之前确认生产过程是统计稳态的,即计算所使用的数据均来自同一个正态总体。一个生产过程是不是会持续保持稳定,回答也是否定的,特别对于机械加工类的生产过程,刀具的磨损、不均匀的热变形等因素会很快导致过程的失稳 (统计不再稳定)。因此,现代生产质量管理应当实时监测过程的运行,当过程出现失稳或有失稳趋势发生时,及时发出报警,通过调节使过程恢复统计稳态。
与逐件检验产品质量的控制方法不同,过程统计控制研究的目的在于保持过程处于统计稳态和及时发现过程运行的变化趋势,从而防止不合格产品的出现,实现预防为主的产品质量管理目标。
1 过程统计控制应用现状
目前生产管理过程中,也有一些推断统计稳态的方法[3-5],比较常用的有 Shewhart控制图、累积和控制图 (CUSUM)和指数加权移动平均控制图(EWMA)等。其中Shewhart控制图应用最为普遍,计算简单,而且有许多商品化的软件可以应用,缺点是研判准则比较复杂,过程均值有小的漂移时,检出效果比较差,对于样本数据量比较少的研究性过程分析以及定量过程分析也都存在一定的不足。累积和控制图(CUSUM)和指数加权移动平均控制图(EWMA)等统计分析工具,虽然它们已被证明在检 测 小 的 漂 移 时 效 果 不 错 外[5-7]。 也 都 存 在 和Shewhart控制图同样的其它缺点。
随着产品特点的不断变化,例如质量要求不断提高,产品的批次增加,单批次的数量减少等原因,对生产过程统计特性分析也提出新的要求。例如在样本数据量少的情况下,对较小的漂移要有比较高的检出精度,统计稳态的的研判更加的简单以及有量化的指标等。
方差分析(Analysis of Variance,简称ANOVA)是从观测变量的方差入手,研究诸多控制变量中哪些变量是对观测变量有显著影响的变量。理论上讲,控制变量可以是主动施加的,也可以是潜在存在的。只要对观测变量产生了显著影响,就可以通过对观测变量的方差分析找到它们。基于这样一个原理,本文运用ANOVA对生产过程进行统计特性分析,建立模型,实现对生产过程的统计稳态研判和连续统计控制。
2 磨削过程的统计特性分析
机械加工过程的输出具有波动性,导致波动的原因有随机的因素,也有非随机的因素。完全的随机因素引起的波动具有正态性,分布形态为对称结构,范围约为±3σ。加入非随机因素的影响往往导致分布形态结构发生改变,在实际生产过程中的后果可能是过程输出超出产品技术规格的控制界,形成不合格品。理想的加工过程应该力求避免非随机影响因素的存在,事实上,完全排除也不现实,非随机影响因素不显著的情况下,可以忽略其影响,把过程的输出看作是正态分布的,或者称过程处于统计稳态。当非随机因素影响显著,过程输出的分布发生漂移,就说生产过程处于统计不稳态,一般来说,统计不稳态的生产过程,其输出超出产品技术规格的概率会增加,不稳态的程度越大,超出技术规格的概率也就越大,出现废品的概率也就越大。
对于大部分机械加工过程来说,在进行正确调试和正确设置工艺参数的条件下都可以达到统计稳态这样一个要求[8-12],不过是需要加以验证的。过程运行中,统计稳态只是相对的,由于不均匀热变形、刀具磨损以及由此引起的振动等原因会导致过程变得不再稳态。
统计特性分析可以识别生产过程中的非随机影响因素,并推断其影响程度,一旦确认影响比较显著时,给出报警并可以采取措施加以消除(消除方法不在本文讨论的范围)。统计特性分析的优势还在于可以通过局部推断总体,即利用有限的样本推断过程总体的变化趋势。另外,统计特性分析也可以检验生产过程是否正确设置了工艺和工艺结构参数以及机床设备是否进行了正确的调试。
3 磨削过程统计控制建模
磨削过程连续统计控制一般在完成初始统计分析之后进行,初始化统计分析确认磨削过程正确设置了工艺和工艺结构参数,确认机床设备进行了正确的调试。另外通过初始化统计分析以后,获得了过程的统计特征参数。
从一个待观察的磨削过程中抽取样本,全部的观测值记作:

式中:k为样本数;n为样本内独立产品观测值的个数。假设数据来自于统计稳态过程,xij服从正态或近似正态分布 N(μ,σ2)。
记各观测值xij与总平均数的离均差平方和为ST,记作:

变换式(1)为式(2)的形式:

展开式(2)并整理得

其中:
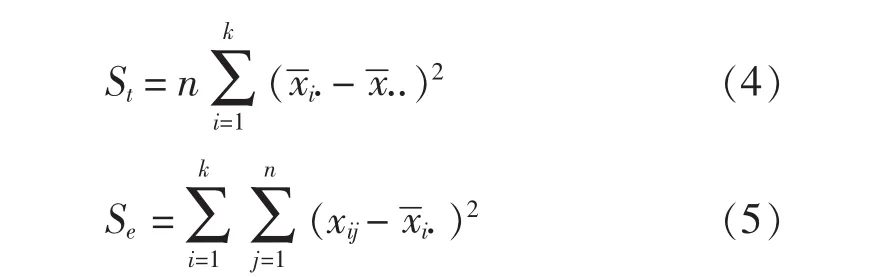
它们分别拥有的自由度为

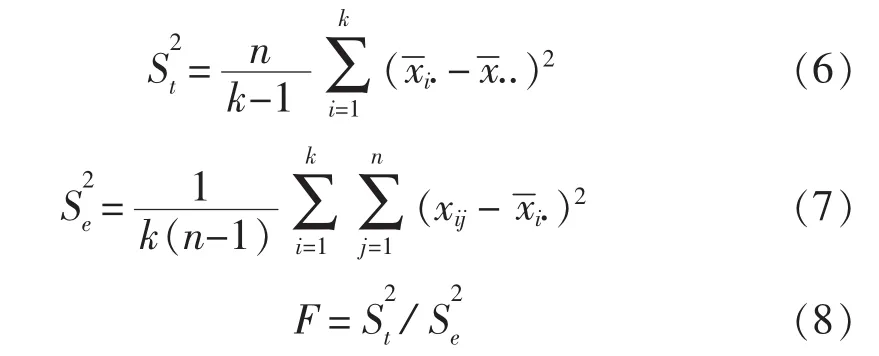
根据 χ2分布定理[13],在样本数据服从正态分布的条件下,和都是随机变量,且分别服从自由度为k1和k2的χ2分布,同样地它们的比值也是随机变量,且服从自由度为k1、k2的F分布。式(8)是基于现场采样数据构建的初始化统计分析模型,其值大小表示不同样本之间的差异显著性,是一个统计稳态的量化指标,但是仅仅依据其大小还不能推断其差异显著程度(过程的统计稳定性),还需要有一个比对的参照系—F分布来加以拟合[13]。
在概率论和统计学里,F分布是一种连续概率分布,被广泛应用于似然比率检验,F分布密度曲线是随自由度k1、k2的变化而变化的一簇偏态曲线,Fα称作右尾临界值,对应的 Fα至+∞的概率值称为右尾临界概率,记作α%,α称作显著性水平,做假设检验时,一般先设定α值,在给定自由度(k1,k2)的条件下,通过数理统计工具资料查出右尾临界值Fα。如果被观察的过程输出分布来自正态过程,式(8)计算出来的F值落在0至Fα区间的概率为(1-α)%,作假设检验一般α取值比较小,F值落在Fα至+∞区间的概率比较小,称作小概率事件,一旦发生,就推断被观测的数据不是来自正态过程,样本之间有显著的差异性,过程统计不稳定,误判的风险不大于α%。
实际的磨削过程仅作初始统计分析是不够的,磨削过程进行中,砂轮的磨损,热变形、振动等影响因素随时会使磨削过程变得失稳或有失稳趋势发生,持续的统计特性分析是必须的。过程投入正式运行以后,需要建立新的统计模型并按适当的间隔采集样本,推断磨削过程是否持续保持在统计稳态。
LSD法称作最小差数检验法,是在F检验的基础上实现连续检验的一种方法,它是将t检验中由所求得的t之绝对值



统计稳态条件下的最小显著差数LSDα则是:


初始统计分析为评价后续过程是否统计稳态提供了基准参考依据。前承后接,有量化的统一标准,有较高的可靠性。LSD法又不同于每次利用2组数据进行多个平均数两两比较的t检验法。它解决了t检验法检验过程烦琐,无统一的试验误差且估计误差的精确性和检验的灵敏性低的问题。
4 实例验证
以某型号柴油发动机零件气门挺杆的磨削加工为例,设备为无心磨床;工艺参数略;生产类型为大批量生产;工件表面粗糙度规格要求为Ra不大于0.25μm。统计稳态验证同时选择工件尺寸和表面粗糙度值作为特征观测值进行研究,限于篇幅,本文仅列出表面粗糙度部分的原始数据和结论。需要说明的是,实际的生产过程也不是每一个工件尺寸都要进行统计过程分析,关联密切的尺寸只分析其中部分即可。产品投入正式生产之前,进行生产过程的统计稳态分析,正式生产后进行连续统计稳态控制。原始样本数据完全取自企业的生产现场,见表1。取α分别为0.01和0.05,初始化统计分析结论见表2。为计算方便起见,所有的误差数据放大一个相同的倍数。
按照一定的时间间隔连续的从后续磨削过程抽取样本,采样数据见表3,并按照LSD方法推断过程的持续稳定性。


表1 原始采样数据
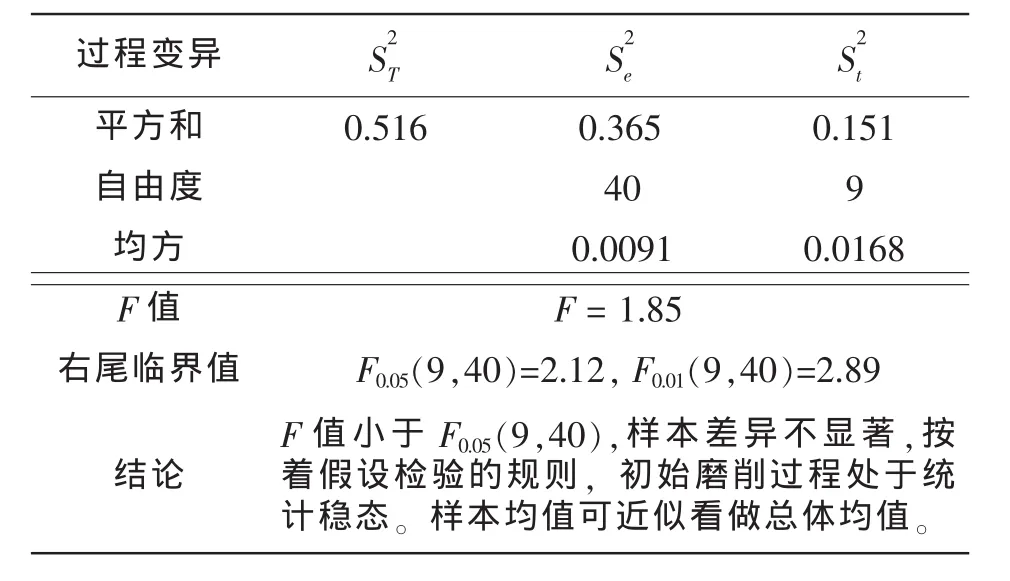
表2 初始化分析数据
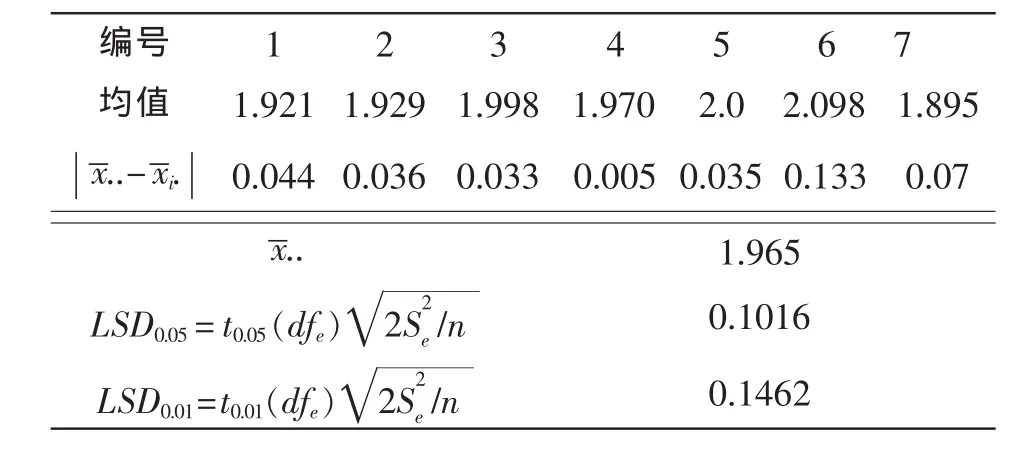
表3 连续的样本数据
5 结束语
通过上述理论推导和实例验证分析,可以归纳得出:应用F检验进行磨削过程统计稳态的假设检验,事实上是一种分布假设检验,以检验均值的变化为主,相较于传统数理统计理论中使用 χ2检验作为分布检验,更符合磨削加工的实际情景。
传统的LSD法主要用于多个处理的多重比较,本文改进后用于连续的过程统计控制,实现过程均值变化的连续监控。
相对于传统的过程统计控制(SPC)方法,基于ANOVA法模型实现了统计稳态的定量分析,简化了过程失稳的判断条件,使判断过程更加的客观、简单和有效,有利于在生产现场推广应用。
[1] 宋祥彦.解读过程能力指数 4个基本特性[J].标准科学,2010(1):33-39.
[2] 韩振鲁,李长河.磨削加工建模与仿真的研究进展[J].磨具磨料通讯,2011(1):7-19.
[3] 于涛,王高山.统计过程控制在先进制造环境中的内涵和作用[J].工业工程与管理,2005(3):51-54.
[4] 陈健.统计过程控制(SPC)在产品质量控制中的应用研究[D].南京:东南大学,2006.
[5] 田学民,曹玉苹.统计过程控制的研究现状及展望[J].石油大学学报:自然科学版,2008,32(4):175-180.
[6] 濮晓龙.关于累积和(CUSUM)检验的改进[J].应用数学学报,2003,26(2):225-241.
[7] 董其义.导弹测试系统统计过程控制方法及其实现[J].海军航空工程学院学报,2009,24(6):666-667.
[8] 钱夕元,荆建芬,侯旭珊.统计过程控制(SPC)及其应用研究[J].计算机工程,2004,30(19):144-154.
[9] 张磊,徐晓辉.砂轮动态磨粒的概率统计数学模型[J].应用科技,2010,37(10):17-20.
[10] 曾伟,无心磨加工机理及工艺参数优化研究[D].武汉:华中科技大学,2006.
[11] 张公绪.新编质量管理学[M].1版.北京:高等教育出版社,1998.
[12] 庞丽君,尚晓峰.金属切削原理[M].1版.北京:国防工业出版社,2009.
[13] 沈恒范.概率论与数理统计教程[M].4版.北京:高等教育出版社,2003.
[14]修世超,李长河,蔡光起.磨削加工表面粗糙度理论模型修正方法[J].东北大学学报:自然科学版,2005,26(8):770-773.
[15] 王维志.无心磨削过程统计特性研究[J].湖北汽车工业学院学报,2011,25(2):35-38.
