一种分形图像编码的改进方法

王文娟

(安徽农业大学理学院数学系,安徽合肥 230036)

一种分形图像编码的改进方法

王文娟

(安徽农业大学理学院数学系,安徽合肥 230036)

在分析小波包变换和分形编码特点的基础上,先将图像进行小波包分解,对进一步细分的高频部分直接进行频域截断,对低频部分进行分形压缩.计算机模拟试验表明,上述方案与基本分形编码方法相比,在重建图像主观质量和运行时间上都显示出优越性.

图像压缩;分形编码;小波包

分形编码典型的缺点是编码时间太长,除算法复杂外,另一个不足之处在于时频局域性差,在高压缩比下容易产生方块效应.而小波包变换能够为信号提供一种更加精细的分析方法,它将频带进行多层次划分,对小波分析没有细分的高频部分也进一步分解,提高了图像的时频分辨率.在图像经过小波包变换后,低频部分能量集中,相比与整个图像只对低频部分进行分形编码可以节省编码时间,而对分解后的高频信号进行一定的频域截断即可达到压缩的目的又在一定程度上可以消除方块效应,“振铃”效应等不良现象,提高图像编码质量.本文即在小波包变换的基础上对分形编码方法进行一定程度的改进.

1 基本分形编码方法

分形图像压缩的数学基础是迭代函数系统(Iterated function system,IFS)理论、压缩映射定理(The constraction mapping thorem)和拼贴定理(the collage theorem)[1].从数学上看,分形编码的原理是简单的,待编码图像由不动点接近它的压缩仿射变换表示,压缩映射原理保证不动点图像由压缩变换迭代作用于任意初始图像来生成,拼贴定理则保证不动点图像是待编码图像的近似图像.其关键在于寻找图像的IFS(迭代函数系统),利用它来达到压缩图像的目的.在分形压缩图像的算法中,一般是先对图像划块分割,然后寻找不同块的自相似块,对目标块和相似块之间的映射进行编码.下面将简要介绍Jacquin的基本分形编码[2].

编码压缩过程：

1.1 图像分割：将原始图像分割成分辨率为B×B(如4×4)像素的互不重叠的值域块(Range块),构成R块池,相邻R块之间没有重叠,它们的并集刚好为原图像.然后再把原始图像分成按步长δ(一般取δ=B)从左到右,从上到下滑动的D×D的定义域块(Domain块),通常D=2B.

1.2 码本构成：依次对每一个Domain块中相邻的4个灰度值求平均(或欠采样),于是每一个大小为D×D(2B×2B)的Domain块就变成了大小为B×B的Sub-Domain块,这些子块的全体就构成码本Ω.

1.3 获取分形码：对每个R块Ri,可以按下面三个步骤在码本Ω中寻找其最佳匹配块Dm(i)：

3)输出当前R块Ri的分形码,即量化参数si,oi,最匹配码字的下标m(i)以及等距变换的序号k.

1.4 输出文件：重复步骤1.3直至所有R块都被编码为止,然后输出量化后的分形码,形成分形编码文件.

解码重构过程：

从任意的初始图像开始(当然该图的大小要与原图一致),和原始图像一样,对任意图像也分为相同大小的定义域块和值域块,根据传输的参数,用值域块对定义域块进行逼近,当全部的定义域块都被逼近一次后,称为完成一次迭代,所得图像作为下一次迭代的初始图像,一直迭代下去直至重构图像不再随迭代发生显著变化为止,重构结束.

2 本文编码方法

小波包变换是小波变换的推广,与小波变换相比,小波包变换能够为信号频带提供一种更加精细的分析方法,其优势主要表现在：(i)能对频带进行多层次划分;(ii)能对多分辨分析没有细分的高频部分进一步分解;(iii)能根据被分析信号特征,自适应地选择相应频带,使之与信号频谱相匹配,从而提高时频分辨率.因此小波包变换具有广泛的应用价值[3].

本文算法的基本思想：由于小波包变换能对图像的高频部分进行进一步的分解,而图像的大部分能力集中在低频部分,从而,可以利用小波包变换的特点,对进一步分解的高频部分根据压缩要求进行截频压缩,只对分解后的低频部分进行分形编解码.高频部分的压缩简单易行且保留了大部分的能量,丢失的部分边缘细节恰好缓和了分形编码出现的方块效应,而只对低频部分进行分形压缩将会大大节省压缩时间,从而达到减少编码时间,改善解码图像视觉效果的目的.

2.1 实验流程.

具体算法如下：

1)先对图像进行如图的小波包分解(以两层分解为例).

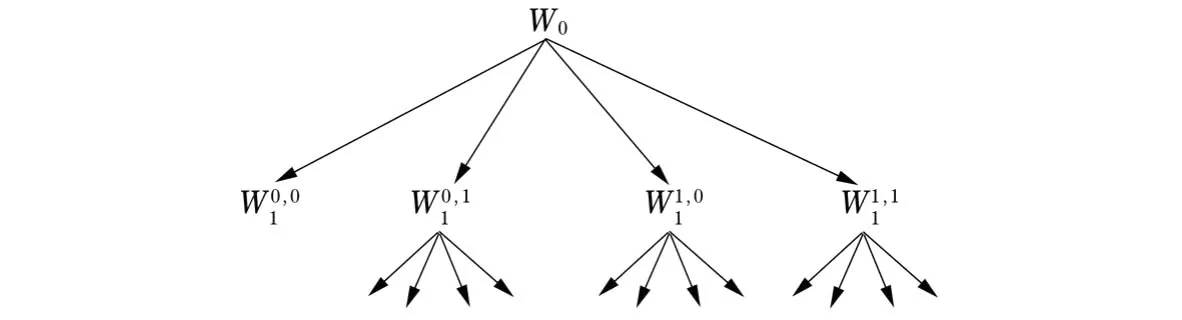
图1 小波包分解

2)提取低频系数W001进行基本分形编码,得到分形码流;同时提取其他系数,进行频域截断,得到小波编码码流.

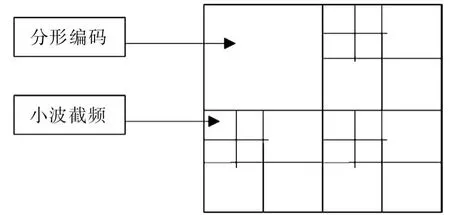
图2 混合编码

3)解码时,分形解码得到低频小波系数;小波逆变换得到其他系数.进行小波包逆变换,得到重构图像.

编解码实验流程图如下：

图3 编解码过程

2.2 实验结果.

实验环境：计算机：Celeron(R)CPU 2.40GHz,内存256M

编程语言：MATLAB 7.0,C++

表1 Peppers图像仿真结果

图4 仿真实现结果(压缩比1∶16)

3 结 论

本算法是对分形图像压缩和小波包变换相结合的一种新的尝试,具有很好的启发和推广意义.从仿真实验结果来看,与基本分形编码算法相比,本算法将编码速度提高了十几倍,并且减弱了基本分形编码易产生的“块效应”,从主观效果上看,本算法解码后的图像质量更好.与现有的其他分形编码的改进方法相比,仿真结果显示出的压缩比不高,主要是因为本算法对分形、小波变换后的系数未进行进一步的量化;另外,本算法是基于固定块分割方案的,对定义域块采用了无覆盖的均匀分割,使得待匹配块质量不够好,所以信噪比不是很突出.对下一步的研究,可考虑将小波变换中发展比较好的零树小波编码推广到小波包图像压缩,而最优小波基的选取[4]以及对人类视觉特性[5]的考虑也是改进方向;另外,结合目前提出的一些快速分形图像编码算法[6-7]也是很好的改进方向.

[1] 李水根,吴纪桃.分形与小波[M].北京：科学出版社,2002：6—39,156—178.

[2] Jacquin A E.Image coding based on a fractal theory of iterated contractive image transformation[J].IEEE Transactions on Image Processing,1992,1(1)：18—30.

[3] 王改梅,刘瑞光,刘芳.基于小波包变换的纹理图像检索[J].计算机工程与应用,2004,40(18)：44—46.

[4] 高永丽.基于图像压缩的小波变换中小波基选择研究[J].电脑与信息技术,2009,17(5),4—5.

[5] 魏玉芬,柳培林,野金花.基于人眼视觉特性的分形小波包图像编码压缩技术研究[J].黑龙江科技信息,2008,20：63-64.

[6] 周一鸣,张超,张曾科.基于图像子块特征的快速分形图像编码算法[J].计算机应用研究,2008,25(2)：458-459, 463.

[7] 裔传俊,徐涛.基于平均偏差的快速分形图像编码[J].计算机工程与设计,2008,29(1)：112-114.

A Study on Improved Fractal Image Coding Algorithm Transformation

WA N G Wen-j uan
(School of Sciences,Anhui Agricultural University,Hefei,Anhui 230036,China)

By analyzing themeritanddisadvantage ofbasic fractal image algorithm and waveletpackage transformation,a new fractal image encoding algorithm was proposed.Firstly the image is decomposed by the wavelet package,then the high frequency part is compressed by wavelet transformation,which utilizes the characteristic of wavelet package analysis;at the same time the low frequency part is compressed through fractal coding technique. Computer simulation shows that the proposed method shows better performance on both the recovery image qualith and running time.

image compression;fractal coding;wavelet package

TN919.81

A

1672-1454(2011)03-0102-04

2008-07-28;[修改日期]2010-03-21