偏微分方程求解的一种新颖方法
——格子Boltzmann模型
2011-11-22乐励华刘唐伟
乐励华, 高 云, 刘唐伟
(东华理工大学数学与信息科学学院,江西抚州 344000)
偏微分方程求解的一种新颖方法
——格子Boltzmann模型
乐励华, 高 云, 刘唐伟
(东华理工大学数学与信息科学学院,江西抚州 344000)
介绍了一种偏微分方程求解的一种新颖方法格子Boltzmann模型,详细分析了它的基本理论和基本原理。并通过不可压Navier-Stokes方程组和二维含源项扩散方程的数值模拟计算实例,说明格子Boltzmann方法的有效性,展示了广阔的应用前景,为今后更深入的研究和广泛应用提供参考.
格子Boltzmann方法;平衡态分布函数;D2Q9模型;Navier-Stokes方程;对流—扩散方程
1 引 言
偏微分方程广泛应用在物理、化学、生物、材料、金融和广大工程技术领域,大学数学的数学物理方程课程也牵涉其中,对偏微分方程求解主要有两种方法:解析方法和数值方法.一般情况下,严格求解偏微分方程是非常困难,仅仅一些具有简单边界或者有比较严格物理限制的现象才能够得到理论解析解.最广泛使用的是数值解法,如有限元(FEM)和有限差分方法(FD)等.格子Boltzmann(LB)方法(也称作格子波尔兹曼方法)是近几十年发展的偏微分方程模拟方法,首先由McNamara和Zanetti在1988年提出,它继承了格子气自动机(Lattice Gas Automaton,L GA)的主要原理并对L GA作了改进,成功地进行了流体力学模拟,对许多问题建立的格子模型,取得了意想不到的效果;一些学者对Navier-Stokes方程,Euler方程,mKdV方程,对流-扩散方程,反应-扩散方程,热传导方程等进行了数值求解计算,也取得了较好的结果.Lattice Boltzmann(LB)方法是一种全新概念的数值求解方法,我们在这里对它做一定的介绍,借以拓宽方程的求解思路,为以后的应用提供良好的借鉴作用.
2 格子Boltzmann(LB)方法模型的建立
2.1 格子Boltzmann方法的主要思想.
这里以二维中常用的D2Q9模型为例,来介绍格子Boltzmann方法.
将流体存在的区域划分为均匀网格,将流体想象成许多只有质量没有体积的微小粒子组成,在同一时刻同一网格节点上,粒子向九个方向运动(如图1),移动到最近的网格节点.其中每个节点上允许一个静止粒子存在,加上与其相邻的有8个节点,所以称为二维九点格子模型,记为D2Q9模型.到目前为止已建立的LBM模型有:D1Q3,D2Q9,D2Q7,D2Q13,D3Q15,D3Q18,D3Q27等(D指维数,Q指粒子运动方向的总数).
其演化过程主要分两个步骤:(a)迁移,粒子从一个节点在一个时间步长内,以恒定的速度运动到相邻节点;(b)碰撞,在一个节点上从相邻节点运动来的粒子发生碰撞,根据质量、动量和能量守恒规则改变粒子的速度,然后各个粒子又以改变后的速度迁移.这两个步骤交替循环,直到流场达到收敛.

图1 二维九点格子模型速度方向以及网格划分
设(X,t)代表在时刻t,位置X=(x,y)处的节点,流体的密度为ρ=ρ(X,t),流体的速度为u=u(X,t),时间步长为Δt,t=0,Δt,2Δt,…,mΔt,格子步长为Δx,粒子迁移速率c=
(cosθi,sinθi)c,(θi=(i-5)π/2+π/4,i=5~8),粒子分布函数fi(X,t)表示节点(X,t)处运动速度为ci的粒子数量,i=0,1,…,8,则粒子分布函数演化过程如下: ,粒子离散速度c0=(0,0),ci= (cosθi,sinθi)c,(θi=(i-1)π/2,i=1~4),ci=

Ωi(f(X,t))称为碰撞算子,表示碰撞引起的变化.Higuera等在1989年作了一个非常重要的简化,假定流场的分布接近于局部平衡状态,并将碰撞操作过程Ωα(f(x,t))进行线性化处理,用单一松弛时间使流场逐渐达到局部平衡状态并且线性稳定;后来,Qian,Chen等学者提出,如果松弛形式采用Bhatnagar-Gross-Krook(BGK)操作就能再现宏观N-S方程,这就是所谓的格子BGK(LBGK)模型,它所对应的LB方程(LBE)是(也称为格子Boltzman模型的演化方程):

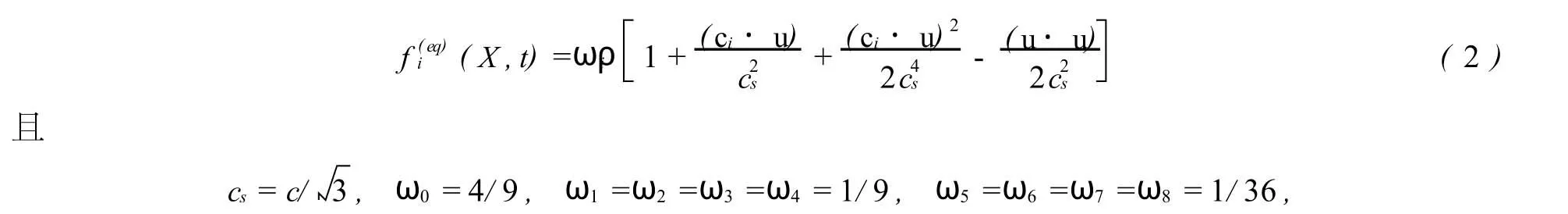
其中τ是松弛时间尺度,控制达到平衡的速度(可根据需要进行设置),由于稳定性的原因,经过实际测算τ必须大于1/2.
事实上不同的网格剖分有着不同的平衡分布函数,LBM建立模型的核心问题就是根据不同的网格确定对应的平衡分布函数和格子Boltzman模型的演化方程,对D2Q9模型,我们就取上面的平衡分布函数.
在节点(X,t)上根据质量和动量守恒规则,流体的宏观密度、速度、压强定义如下:
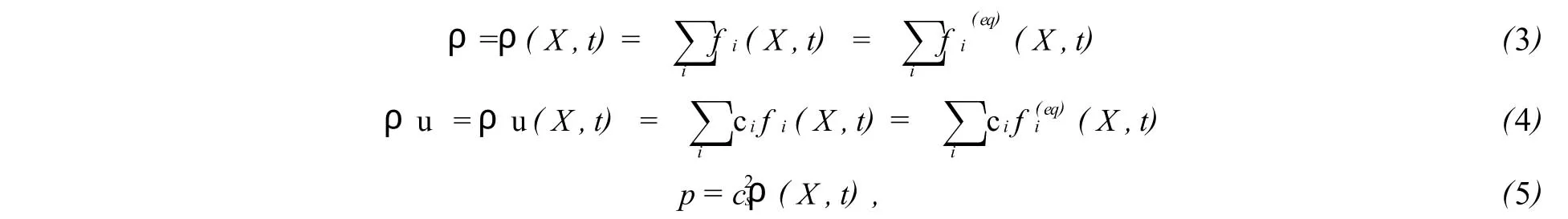
另外满足动量通量守恒法则

其中I为二阶单位矩阵.
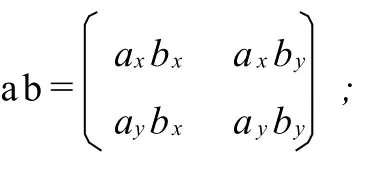

2.2 从Lattice Boltzmanm模型再现宏观流场控制方程.
格子法建模的核心就是确定对应网格的平衡分布函数,而建模成功与否,看格子Boltzmann模型能否恢复宏观流场控制方程.下面以Lattice BGK(LBGK)模型对Navier-Stokes方程(简称N-S方程)恢复为例加以说明.
这里简单介绍多尺度分析Chpamna-Enskog展开,Chpamna-Enskog展开法本质上是一种多尺度方法,基本思想是将时空变量用多层次时空尺度来表示,而在各级尺度上,物理量的量级一致.我们进行Chapman-enskog展开:
假设系统虽然没达到平衡态,但在局部小体积中已离平衡态不远,因此可假定分布函数的展开

引入两个宏观时间尺度t1=εt,t2=ε2t,一个宏观空间尺度x1=εx,则算子的展开



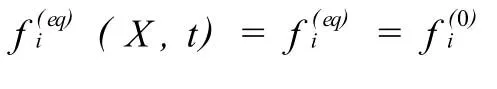


(26)与(28)正是不可压Navier-Stokes方程组(简称N-S方程).
2.3 格子Boltzmann方法的计算流程.
i)为流场内的每一个格子设置初始条件(密度、速度、压强等),选择合适的时间松弛尺度τ;
ii)对于每个格子,用式(3)和式(4)计算它们的宏观区域中的密度和速度的变化;
iii)用式(2)计算平衡态分布函数;
iv)把格子分布函数和平衡态分布函数代入式(1);
v)根据步骤iv)的结果,对各个相邻格子进行相应的调整;
vi)根据边界条件来调整分布函数;
vii)返回步骤ii)进行循环执行,直到流场达到收敛要求.
接下来我们以两个定解问题为例,验证上面方法的正确性和可行性.
3 格子Boltzmann方法数值模拟不可压Navier-Stokes方程组
设某流场流动区域为0≤x≤2π,0≤y≤0.16π,流体的速度为u=(u(x,y,t),v(x,y,t)),流体的压强p=p(x,y,t),满足不可压Navier-Stokes方程组,即·u=0,+u·u=-狆+2u,其定解问题如下:

其中A,B,k,p0为常数,可以验证该问题具有如下解析解:
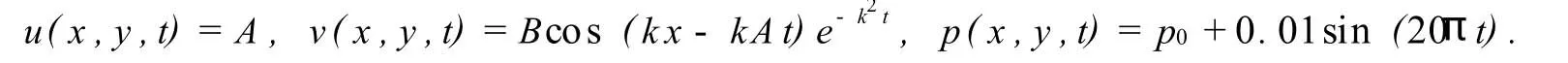
用Lattice Boltzmann方法进行数值模拟,模拟中不妨取A=B=k=1.0,p0=3.0,模拟三个不同时刻t=0.018277和t=0.18277,t=1.8277在y方向上的分量v(x,y,t)如图2,图上画出v(x,y,t)在通过流场中心(y=0.08π)模拟结果与解析解,可以看到模拟结果与解析解在不同时刻都吻合得很好.

图2 y方向速度分量v(x,y,t)在t=0.018277和t=0.18277,t=1.8277时刻的模拟解与解析解相比较
4 格子Boltzmann方法数值模拟含源项的扩散方程
二维含源项对流-扩散方程的一般形式如下:
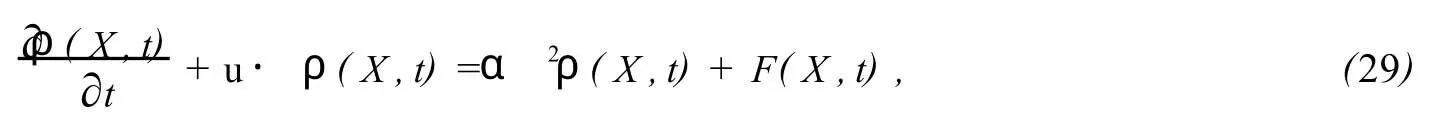
其中u=(u1,u2)是一个2维的常向量,代表对流速度;α是扩散系数,是一常数;X=(x,y)是空间的坐标,t代表时间;ρ(X,t)是物质在空间点x和时刻t的密度;F(X,t)是在空间点x和时刻t的源项;当u=0时,方程(29)就变为含源项的扩散方程.
仍采用D2Q9模型,由于方程有改变,对应的LB模型有所调整,这是关键,主要变化是格子Boltzman模型的演化方程(1).采用的演化方程为


用格子Boltzmann方法进行数值模拟,模拟中不妨取l=1,α=0.001,模拟两个不同时刻t=0.1和t=0.3在y=0.5处的密度ρ,如图3,可以看到模拟结果与解析解在不同时刻都吻合得很好.
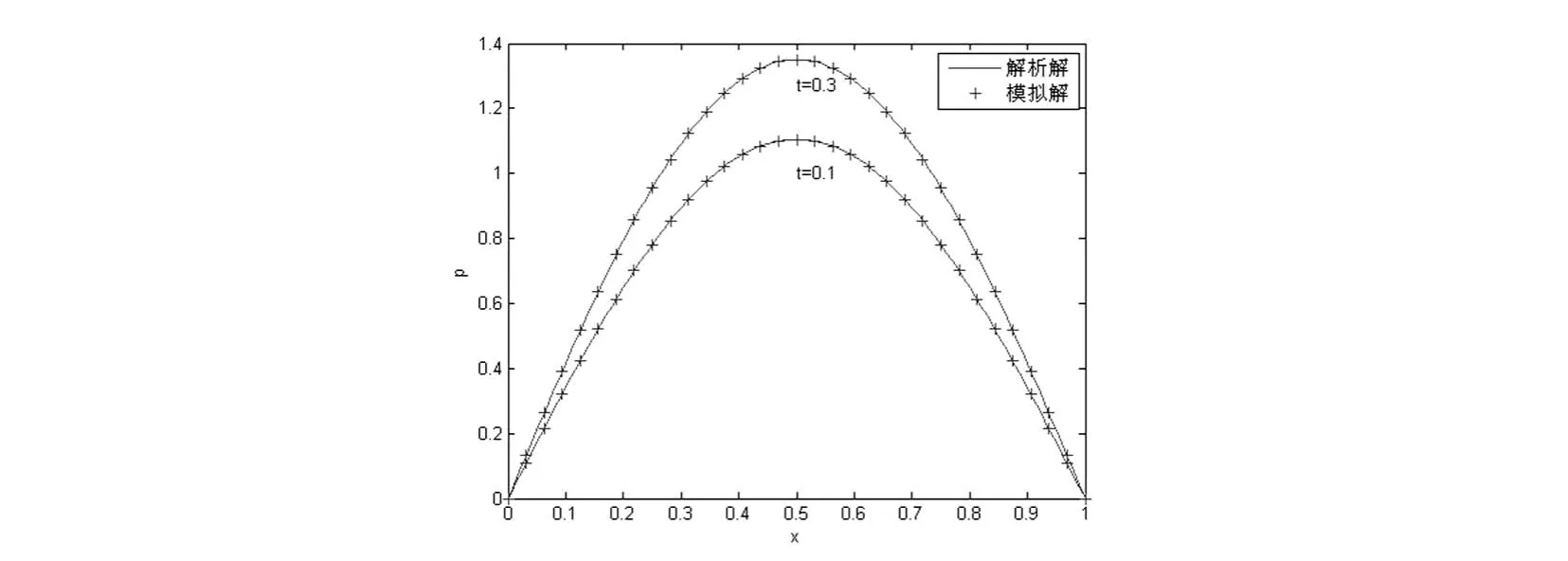
图3 密度ρ在t=0.1和t=0.3时刻在y=0.5处的模拟解与解析解相比较
5 结 语
本文初步介绍了Lattice Boltzmann方法的理论,作为一种新的模拟和建模方法,其理论思想简单,入门门槛不高,具有微积分和一些场论基础就行.格子波尔兹曼方法打破传统的数学建模观念,不需建立和求解复杂的偏微分方程,是一种高效建模数值方法,具有广阔应用前景,其研究已从纯粹的理论试验领域迈向工程应用,在生物流体、磁流体、交通流、燃烧、微尺度流动、化工、图像处理、量子力学、纳米流体以及光学、声学等众多领域得到了应用,形成了一个国际研究热点.目前格子Boltzmann方法还处于不断发展之中,作为一种新生事物,人们对它还缺乏了解和比较陌生,需要大量的论证和实践,挖掘其潜力,开拓新的应用领域,作为我们数学工作者是一个很好的切入点,很值得我们去做进一步的研究工作.
[1] McNamaraG R,Zanetti G.Use of the lattice Boltzmann equation to simulate lattice-gas automata[J].Phys.Rev. Lett.,1988,61:2332-2335.
[2] GuoZhaoli,Shi Baochang,Wang Nengchao.Lattice BGK model for incompressible Navier-Stokes equation[J].Journal of Computational Physics,2000,165:288-306.
[3] Deng Bin,Shi Bao-chang,Wang Guang-chao.A new lattice Bhatnagar-Gross-Krook model for the convection-diffusion equation with a source term[J].Chin.Phys.Lett,2005,22:267-270.
A Novel Method for the Partial Differential Equation to Solve—Lattice Boltzmann Model
L E L i-hua, GAO Yun, L IU Tang-wei
(School of Mathematics&Information Science,East China Institute of Technology Fuzhou,Jiangxi 344000,China)
We introduce a novel method for the partial differential equation to solve-Lattice Boltzmann model,The basic theory and basic principle of LBM is analyzed in detail.Two results illustrate that Lattice Boltzmann method is right,effective through numerical simulation on incompressible Navier-Stokes equation and the 2-dimensional diffusion equation with the source term,that shows a wide application prospect to us,which probably provides reference for intensive research and extensive applications later on.
lattice Boltzmann method;equilibrium distribution functions;D2Q9 model;Navier-Stokes equation; convection-diffusion equation
O241.82
A
1672-1454(2011)03-0075-08
2008-08-28
国家自然科学基金项目“复杂流动的格子Boltzmann建模与计算机仿真”(60773195);中国科学院边缘海地质重点实验室开放研究基金课题“孔隙裂隙介质中多相流体逾渗模型及数值模拟”(2010.1—2011.12)
