基于蚁群优化的超声波电动机系统动态模糊辨识建模

吕 琳,史敬灼

(河南科技大学,河南洛阳471003)

0 引 言

建立超声波电动机系统模型可采用不同方法,从适合于控制应用的角度出发,控制建模方法研究日益受到重视。通常,为便于在线实现并尽量减小在线计算量,控制模型应相对简单并能够表征超声波电动机系统控制非线性的主要方面。由于理论建模的局限性,控制建模通常以基于实验数据的辨识方法为主[1-2]。根据模型辨识方法的不同,模型的形式可以是传递函数、差分方程、神经网络等。

近年来,基于模糊逻辑理论的模糊建模方法逐渐兴起,为非线性复杂系统建模提供了另一有效途径。模糊建模方法在电机领域的应用还不多,更多的是采用模糊方法实现转速或位置控制。

本文研究超声波电动机系统动态模型的模糊建模方法。论述了超声波电动机系统的模糊建模方法与过程,给出了采用蚁群优化确定模糊聚类隶属函数的方法,并用最小二乘法辨识模糊规则结论部分的待定参数,建立了能够表征超声波电动机驱动电压幅值、频率与其转速之间非线性动态关系的二输入单输出Takagi-Sugeno(以下简称T-S)模糊模型。

1 建模所需数据的实验测取

实验系统框图如图1所示。实验用电机为Shinsei USR60型两相行波超声波电动机,H桥相移PWM驱动电路。控制部分采用DSP为主控芯片,用于实现控制算法,包含分别用于控制两相驱动电压幅值的A、B相电压闭环控制器,以及通过调节驱动频率实现转速控制的转速闭环控制器。图中,Nref、Uref分别为转速、驱动电压幅值的给定值。设定Nref测取转速阶跃响应,其间调节Uref以改变电机驱动电压的幅值大小;随着驱动电压幅值的变化,在转速闭环控制作用下,频率必然改变以维持电机转速为Nref;同时记录Uref、频率及转速的动态变化过程,得到一组数据。改变Uref调节方式、Nref数值,重复上述过程,测得多组数据用于建模。

图1 转速控制实验系统结构

2 超声波电动机系统模糊建模方法

一般地,T-S模糊模型的基本结构如图2所示,包含输入量化、模糊化(隶属度计算)、基于模糊规则的模糊推理和输出比例运算等基本环节。其模糊规则形式如下,前提条件是模糊的,结论是清晰值。

图2 模糊模型基本结构

Ri:If(x1isAi1)and(x2isAi2)and…and(xrisAir),theny=ai0+ai1x1+ai2x2+…+airxr

规则中,Ri代表第i条模糊规则。xk是模糊模型的第k个输入变量,Ajk是变量xk的第j个模糊子集,yi是第i条规则Ri的输出,aij是结论部分待定参数。

建立超声波电动机系统的T-S模型,需要根据实测输入、输出数据进行结构辨识和参数辨识。参数辨识指规则前提部分和结论部分的参数辨识。参数辨识是在一定的模糊推理结构约束下,确定最优的模型参数,以使模型输出尽量接近实测数据的优化过程。结构辨识是参数辨识的基础。首先要确定输入变量及输入论域空间;然后,可采用模糊网格、模糊聚类、模糊树等算法进行输入空间的模糊划分。其中,模糊聚类算法最为常用,它用隶属度描述向量属于一个聚类的可能性。首先,设定一个聚类数,该聚类数既是隶属函数个数也是规则数;然后对输入空间进行模糊划分,采用蚁群算法确定高斯型隶属函数的中心、宽度等特征值,即可完成超声波电动机系统T-S模型的结构辨识。T-S模型结论部分的待定参数可用最小二乘法辨识得到。模型建立后,进行验证计算,如果模型输出值误差较大,则增加规则数重新进行建模。建模基本步骤如下:

(1)确定输入变量及个数p、聚类数c;

(2)根据实测的建模数据,确定驱动电压幅值、频率和转速对应的论域区间[M-,M+];

(4)计算各数据点xk与聚类中心的距离dik:

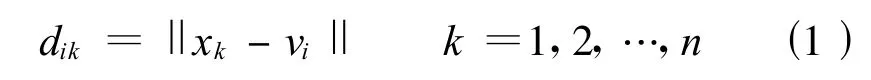
(5)计算建模数据的隶属度μik:

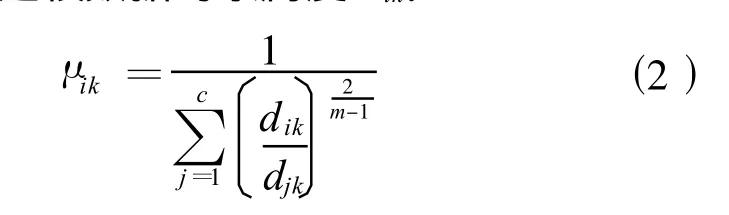
式中:m为常数,通常取m=2。

(6)采用最小二乘法求得T-S模型结论部分的待定参数aij;

(7)进行模型验证。若模型精度不理想,则改变输入变量个数p和/或聚类数c,转步骤(2)。

根据实测数据分析,确定模型输入变量为当前及以前时刻的驱动电压幅值(峰峰值)u(k-3)、u(k-2)、u(k-1)、u(k),频率值f(k-3)、f(k-2)、f(k-1)、f(k)和转速值n(k-2)、n(k-1);输出变量为当前时刻的转速值n(k)。输入变量个数p=10,规则数(亦即聚类数)c=10。u(k-3)、u(k-2)、u(k-1)、u(k)的隶属函数是一样的,各有10个高斯型隶属函数,f(k-3)、f(k-2)、f(k-1)、f(k)和n(k-2)、n(k-1)也各有10个隶属函数,共30个隶属函数。每个隶属函数有宽度和中心等2个待定参数,所以共有60个待定参数需要通过蚁群算法优化获得。

3 用于超声波电动机模糊建模的蚁群算法

所建动态模糊模型中,高斯型隶属函数的中心和宽度等参数共有60个。期望通过基于实测数据的动态优化过程,获取如此多的优化参数值,需要慎重选择适当的优化算法以得到确实有效的优化结果。另一方面,超声波电动机本身的显著非线性,必然使得作为优化目标的模糊模型具有较高的复杂性;这进一步增加了优化过程的复杂度。

蚁群算法是一类内含随机性的群体智能优化算法。因其在解决复杂优化问题方面表现出的良好性能,蚁群算法的应用领域正在不断拓展[3-4]。假定有q个待优化的参数,分别为a1,a2,…,aq。首先,对每一个参数ai(1≤i≤q)将其设置为可能取值范围内的Q个非零随机数,形成集合Wai。蚁群从蚁巢出发去寻找食物,每只蚂蚁都从集合Wa1出发,根据集合中的每个元素的信息素选择一个值,在全部集合中选择一组值,当蚂蚁在所有集合中完成元素选择后,它就到达食物源并按原路返回蚁巢,同时调节集合中元素的信息素。反复进行这一过程,当达到给定的迭代次数或者性能指标时,寻优过程结束。

采用蚁群算法优化超声波电动机T-S动态模糊模型中的隶属函数参数,计算步骤如下。

(1)分别在u、f和n的取值范围内随机产生100个非零数,组成60×100矩阵;

(2)初始化参数。设定蚂蚁个数m,信息素的残留程度ρ(0≤ρ＜1),信息素总量Q,最大循环次数Nm,令每个集合中每个元素的信息素τj(Wai)=C(C为常数),Δτj(Wai)=0,j=1,2,…,100。τj(Wai)表示集合Wai的第j个元素的信息素,Δτj(Wai)=0表示在本次循环中集合Wai上的第j个元素上的信息素的增量;

(3)第k只蚂蚁从集合Wa1出发(k=1,2,…,m),根据移动概率独立随机的从集合Wai中选择第j个元素。移动概率计算如下:

当第k只蚂蚁在所有集合里完成元素的选择后,就到达食物源。

(4)重复步骤(3)。m只蚂蚁在所有集合里完成元素的选择后,按照每只蚂蚁选择的元素,即超声波电动机T-S动态模糊模型中的隶属函数参数,根据输入数据计算模型输出,与实测数据比较得到误差,进而得到每只蚂蚁的性能指标如下:

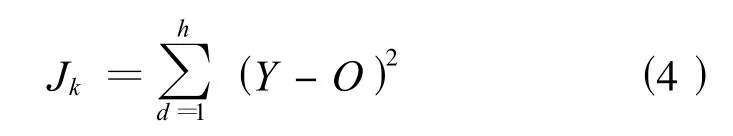
式中:Y为模型输出;O为实验数据;d=1,2,…,h,h为实测数据点个数。记录本次循环中性能指标的最小值,并记录该值对应的蚂蚁所选择的元素;

(5)更新信息素

式中:Δτkj(Wai)表示第k只蚂蚁在本次循环中留在集合Wai上的第j个元素上的信息素;τj(next)(Wai)为更新的信息素,用于下一次循环中;ek是第k只蚂蚁的最大输出误差:

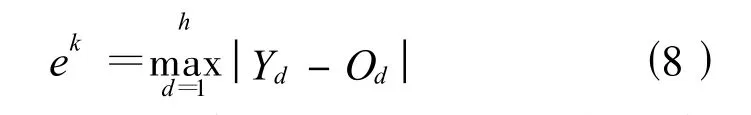
(6)当所有蚂蚁都完成元素的选择,更新信息素后,完成一次循环。重复步骤(3)～(5),直到指定最大循环次数Nm或者达到指定的性能指标值Je,循环结束,并输出最优解。

4 蚁群优化模糊建模

蚁群优化算法中,蚂蚁个数m、信息素残留程度ρ等参数对优化过程具有重要影响,甚至会影响优化算法的有效性。但是这些参数的取值与优化对象密切相关,至今没有明确的方法;通常需要针对特定的优化对象,通过尝试逐步寻求适当的m、ρ等参数取值,以加快优化进程、改善优化结果。

4.1 蚂蚁个数m的确定

设定ρ=0.7,取信息素总量Q=100,m分别取为40、50、60和80,通过比较优化过程及优化结果,寻找合适的m值。优化过程退出条件设定为固定循环次数,即当优化循环次数达到预先设定的最大循环次数Nm时,输出最优解,优化过程结束。此处,取Nm=150。考虑到蚁群优化过程中包含随机因素,对每个m值各进行三次优化计算,每次得到一个最优解及对应的最小性能指标Jmin,同时记录优化过程所用时间。对三次优化计算所得最小性能指标Jmin取平均值,可作为衡量优化效果好坏的依据。

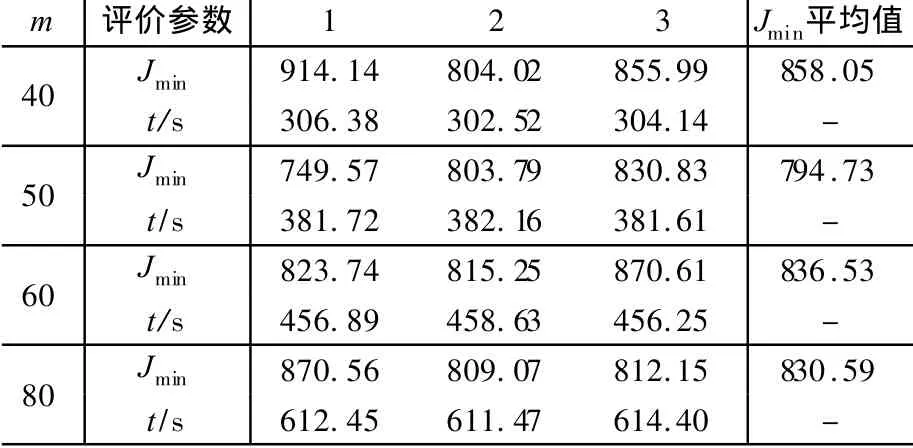
表1 不同m值的优化过程对比

表1给出了上述优化计算的结果。计算所用计算机的CPU为Pentium 4,主频2.93 GHz,内存容量为512 MB。可以看出,随着蚂蚁数的增加,计算时间变长;m=50和m=80情况下的Jmin平均值较小。下面改变优化过程退出条件,比较m=50和m=80的优化效果,确定优化效果较好的蚂蚁数。

表1中,Jmin值通常大于800;因而设定退出条件为Jmin≤800或Nm＞1000。其中,最大循环次数Nm设定为1 000,以限制优化过程时间长度。改变退出条件后,分别在m=50和80的情况下,进行三次优化运算,得到结果如表2所示。可以看出,m=80时,三次优化计算所得最小性能指标Jmin均达到800以下,且计算所用时间明显少于m=50情况。至此可以确定,蚂蚁个数m取为80较为合适。

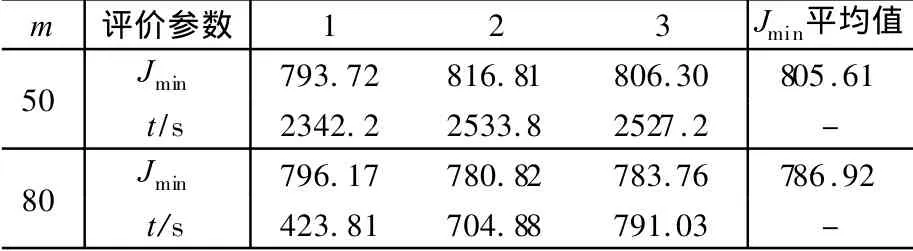
表2 m=50和m=80情况下的优化过程对比

4.2 信息素残留程度ρ的确定

设定m=80,信息素总量Q=100,最大循环次数Nm=200,ρ分别取为0.3﹑0.5﹑0.7和0.9,分别进行三次优化计算,得到结果如表3所示。

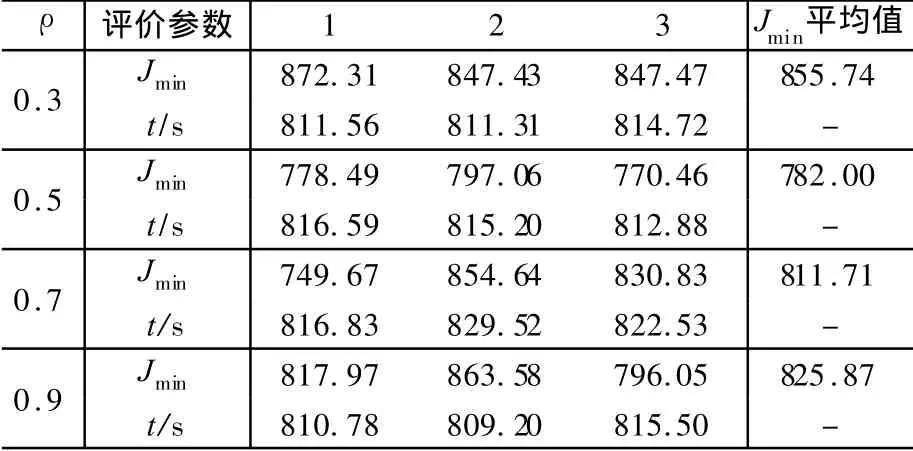
表3 不同ρ值的优化过程对比

表3表明,由于循环次数及m值固定,每次优化过程的计算时间基本相同。在ρ=0.5时,Jmin平均值最小,表明优化效果较好。由此可以确定,在循环次数Nm=200的情况下,取ρ=0.5,可以得到较好的优化效果。可以考虑增大循环次数,看是否能得到一个更小的性能指标,使优化效果更细想。

下面,在m=80、ρ=0.5的情况下,改变退出条件,期望得到更好的优化结果。根据表3的Jmin值情况,将退出条件中的性能指标设定为Jmin≤700。为了避免出现计算时间过长的情况,将最大循环次数设为2 000。故退出条件为Jmin≤700或Nm＞2 000。经过优化计算,得到最优解,对应的Jmin值为662.1,计算过程历时935.55 s。

根据上述最优解,得到超声波电动机动态T-S模糊模型中输入变量u、f和n的高斯型隶属函数参数。模型计算输出与实验数据对比如图3、图4所示。图3、图4中,模型输出的最大相对误差值分别为1.4%、1.2%,平均误差为0.68 r/min、0.65 r/min,较好地反映了超声波电动机的动态特性。

图3 模型输出与实测数据对比(nref=70 r/min)

图4 模型输出与实测数据对比(nref=90 r/min)

5 结 语

蚁群算法可以有效避免局部优化,寻优方法简单高效,鲁棒性强。本文利用蚁群算法对超声波电动机系统T-S动态模糊模型参数进行优化,得到了较为满意的效果。

[1] Tomonobu S,Mitsuru N,Naomitsu U,et al.Mathematical model of ultrasonic motors for speed control[J].Electric Power Components and Systems,2008,36(6):637-648.

[2] Chen T C,Yu C H.Generalized regression neural-networkbased modeling approach for traveling-wave ultrasonic motors[J].Electric Power Components and Systems,2009,37(6):645-657.

[3] 王旭东,刘金凤,张雷.蚁群神经网络算法在电动车用直流电机起动过程中的应用[J].中国电机工程学报,2010,30(24):95-100.

[4] 王志强,刘刚.高速无刷直流电机锁相转速控制器参数蚁群优化[J].微电机,2010,43(6):54-58.