一类非线性二层规划问题的神经网络方法

洪云飞

(长江大学期刊社；长江大学信息与数学学院，湖北 荆州 434023)

吕一兵

(长江大学信息与数学学院，湖北 荆州 434023)

一类非线性二层规划问题的神经网络方法

洪云飞

(长江大学期刊社；长江大学信息与数学学院，湖北 荆州 434023)

吕一兵

(长江大学信息与数学学院，湖北 荆州 434023)

研究了下层为凸规划的一类非线性二层规划问题的神经网络方法。在下层问题为凸规划的情况下,将下层问题用其K-T最优性条件代替，从而把原二层规划转化为单层非线性规划；构造该单层规划的罚函数，提出求解该类规划问题的神经网络方法。数值试验结果表明该方法是可行和有效的。

非线性二层规划；罚函数；K-T最优性条件；神经网络

在对多层规划的研究中，二层规划是一个重要的研究对象。二层规划研究的是具有2个层次系统的规划与管理问题，上层决策者只是通过自己的决策去指导下层决策者，并不直接干涉下层的决策；而下层决策者只需要把上层的决策作为参数，它可以在自己的可能范围内自由决策。二层规划的基本形式为：

式中，x、y分别称为上下层变量；F、f分别称为上下层目标函数；g、G分别称为上下层约束函数。当F、f、G、g全为线性函数, 则称为线性二层规划；否则称为非线性二层规划。

一般来说，求解二层规划问题是非常困难的，文献[1]指出线性二层规划是一个Np-hard问题，文献[2-4]对此结论给出了证明。对于一般的非线性二层规划问题, 文献[5-6]提出了基于下层问题的K-T最优性条件的求解方法。下面笔者主要研究F、f、G、g连续可微且f、G关于变量y是凸函数的一类非线性二层规划问题：鉴于文献[5-6]中的方法，将下层问题用其K-T最优性条件代替，从而将原二层规划化为单层非线性规划, 构造该单层规划的罚函数，进而提出求解该类规划问题的神经网络方法。

1 非线性二层规划问题的转化

考虑如下线性约束的非线性二层规划问题：

其中，x∈Rn，y∈Rm，F:Rn×m→R1，f:Rn×m→R1，P∈R(n+m)×(n+m)，c∈Rn，d∈Rm，Q∈Rm×m，D∈Rm×n，b∈Rm，A∈Rq×n，B∈Rq×m，r∈Rq。

定义1对于线性二层规划问题，称集合：

S={(x,y)|Ax+By-r≤0,x≥0,y≥0}

为其约束域。

对于固定的x，当下层问题满足Slater条件，由凸规划的最优性理论可知，下层规划问题可以转化等价如下Kuhn-Tucker最优性条件稳定点问题：

Qy+Dx+b+λTB=0λT(Ax+By-r)=0λ≥0Ax+By-r≤0

(2)

式中，λ=(λ1,…,λq)T是广义拉格朗日乘子。用式(2)替换式(1)中的下层问题得：

记h(x,y,λ)=(Qy+Dx+b+λTB,λT(Ax+By-r))T，则问题(3)可简写为下格式：

2 非线性二层规划问题的神经网络模型

定义2问题(4)的罚函数[7]定义为：

(5)

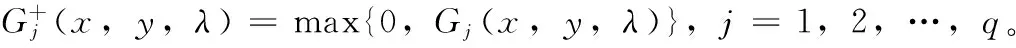
由此问题(4)可以对应转化为如下罚函数优化问题：

记X=(x,y,λ)T，由式(5)则可定义其能量函数[7,8]为：

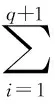
(6)

根据神经网络理论，将优化设计变量与神经元输出相对应，构造神经网络的非线性微分方程(动力系统)为：

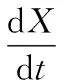
(7)

由式(6)和式(7)可得到能量函数随时间的变化率为：

(8)

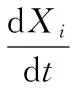
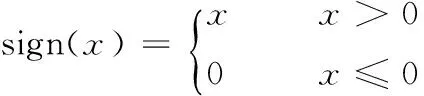
因此，式(7)可以具体化为：

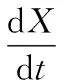
(9)

定理1若X*是网络动力系统(7)或(9)在罚因子M下的平衡点，对于X≠0有E(X)≠0，则X*是网络动力系统(7)或(9)的稳定点，且为罚函数优化问题的局部最优点。若X*是罚函数优化问题的一个最优解，则X*是网络动力系统(7) 或(9)的在罚参数M下的平衡点。

定理1前一部分由式(8)可知是成立的，后一部分显然成立。

3 数值试验

考虑其理论最优解为如下的非线性二层规划问题:

使用定步长四阶龙格库塔法求解上述问题的神经网络动态方程(9)。选取初值为(x,y,λ1,λ2,λ3)=(5，5，1，1，1)，罚因子M=10000，步长为10-5，得到图1。

图1 x、y、λ随时间的变化曲线

从图1中可以看到曲线最终都达到稳定状态，由该方法得到最终的计算结果为(x,y,λ1,λ2,λ3)=(5.104，1.891，0.000，-0.000，5.870)，所以用神经网络方法求得的优化解为(x,y)=(5.104，1.891)。数值试验结果表明，神经网络最终达到稳定状态，可以得到非线性二层规划问题的最优解。

4 结 语

给出了下层为凸规划的一类非线性二层规划问题的神经网络方法，该算法的设计比较简单，易于编程实现，同时值得注意的是利用罚函数构造神经网络模型使得系统变量较少，同时可增大罚因子的值以加快网络的收敛速度。但是在数值试验的过程中，选取不同的初值对神经网络的最终稳定状态有不同的影响，尤其当选取决策变量的初值较小时，将得不到最优解的稳定状态，而且罚因子过小起不到惩罚作用，过大又受机器性能影响。因此，该非线性二层规划问题的神经网络方法的全局稳定性研究方面以及初值有待进一步深入。

[1]Jeroslow R.The polynomial hierarchy and a simple model for competitive analysis[J].Mathematical programming，1985，32(2)：146-164.

[2]Ben-Ayed O，Blair C E.Computational difficulties of bilevel linear programming[J].Operations Research，1990，38(3)：556-560.

[3]Bard J.Some properties of the bilevel programming problem [J].Journal of Optimization Theory and Applications.1991，68(2)：371-378.

[4]Hansen P，Jaumard B，Savard G.New branch and bound rules for linear bilevel progra-mming [J].SIAM Journal scientific and statistical computing，1992，13(5)：1194-1217.

[5] Lv Yibing，Hu Tiesong，Wang Guangmin，et al.A penalty function method based on Kuhn-Tucker condition for solving linear bilevel programming[J].Applied Mathematics and Computation，2007，188(1)：808-813.

[6]吕一兵，陈忠，万仲民，等.非线性-线性规划问题的罚函数方法[J].系统科学与数学，2009，29(5)：630-636.

[7]孟志青，胡奇英，杨晓琪.基于精确罚函数的一类广义非线性神经网络模型[J].自动化学报，2003，29(5)：755-760.

[8]任丽君.基于罚函数法的神经网络优化设计研究[J].绍兴文理学院学报，2006，26(10)：36-39.

[编辑] 李启栋

10.3969/j.issn.1673-1409.2011.12.002

O224

A

1673-1409(2011)12-0004-03