具变指标反应项的抛物和双曲方程的爆破性质

唐树乔

(东南大学数学系，江苏 南京 211100; 亳州师范高等专科学校理化系，安徽 亳州 236800)

具变指标反应项的抛物和双曲方程的爆破性质

唐树乔

(东南大学数学系，江苏 南京 211100; 亳州师范高等专科学校理化系，安徽 亳州 236800)

研究了带有变指标反应项的非线性抛物和双曲方程正解的爆破性质，证明了存在初值使得相应解在有限时刻爆破。

爆破；变指标；非线性抛物方程；非线性双曲方程

对非线性抛物方程:

(1)

有学者对方程(1)解的爆破问题进行了大量深入的研究，如爆破准则、爆破的速率和剖面、最大存在时间、爆破后的连续性等[1-2]。抛物问题(1)出现在应用数学的好几个分支中，并且已经应用到化学反应模型、热传学和群体力学。

考虑下列既带有变指标反应项又带有固定指标反应项的非线性抛物方程：

(2)

其中，Ω⊂RN是带有光滑边界∂Ω的有界区域；k>1；q>1；p(x)和u0(x)是非负连续有界函数且u0(x)不恒等于0。近年来，带有变指标反应项的非线性抛物方程得到了人们的广泛关注[3-6]。对于k=-1时方程(2)的情形，刘云霞[7]也给出了解在有限时刻爆破和整体存在的条件。令：

笔者研究了带有变指标反应项的非线性抛物和双曲方程正解的爆破性质，证明了存在初值使得相应解在有限时刻爆破。

1 非线性抛物方程

1.1有限时刻爆破

引理1设η(t)为连续可导函数且满足不等式：

η′(t)≥-aη(t)+bηq(t)-c

其中，常数q>1,a,b,c>0。若η(0)>0,-aη(0)+bηq(0)-c>0，则η(t)爆破。

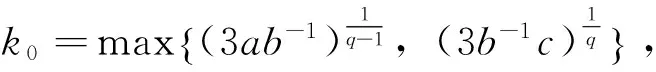
定理1设Ω⊂RN是带有光滑边界∂Ω的有界区域，u(x,t)是方程(2)的正解，p(x)和u0(x)是非负连续有界函数，那么当p->q>1时，对于充分大的初值u0(x)，存在有限时间T>0使得:

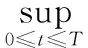
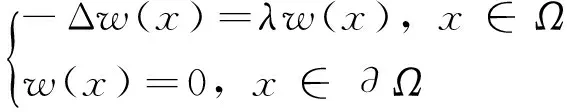
(3)

对于每一个t>0，把Ω分成2个集合：

Ω1={x∈Ω:u(x,t)<1}Ω2={x∈Ω:u(x,t)≥1}

于是：

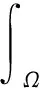
根据Ω2的定义，可以得到：

(4)

其中c2>0。令：

联合不等式(3)和(4)可得：

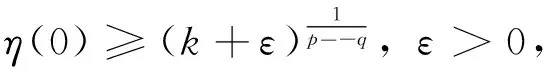
η′(t)≥-λ1η(t)+εηq(t)-c2

于是，由引理1可以知道，方程(2)的正解u(x,t)在有限时刻爆破。

1.2整体存在性

定理2设Ω⊂RN是带有光滑边界∂Ω的有界区域，p(x)是非负连续有界函数，那么当p(x)≤1时，方程(2)的正解u(x,t)对任意初值整体存在。

证明当p(x)≤1时，构造函数v(x,t)=(‖u0‖∞+1)et。则：

vt(x,t)=(‖u0‖∞+1)et≥(‖u0‖∞+1)p(x)etp(x)≥Δv+vp(x)-kuq

且：

v(x,0)=‖u0‖∞+1≥u0v(x,t)=(‖u0‖∞+1)et≥0x∈∂Ω

从而v(x,t)为方程(2)的上解，所以方程(2)的正解u(x,t)对任意初值整体存在。

2 非线性双曲方程

下面，笔者将讨论以下非线性双曲方程：

(5)

的正解在有限时刻爆破的性质。其中，u0(x)≥0,u1(x)≥0,并且它们都不恒等于0。

引理2[8]设y(t)∈C2满足y″≥h(y(t))，y(0)=α>0,y′(0)=β>0,对于所有的s≥α都有h(s)≥0，那么y′(t)>0且：

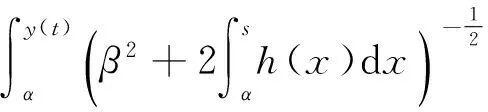
定理3设u(x,t)∈C2是方程(5)的解，p(x)是非负连续有界函数，那么当p->q>1时，对于充分大的初值u0(x)和u1(x)，存在有限时间T>0使得：

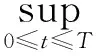
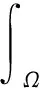
由Höld不等式，可以推知：

(6)

对于每一个t>0，把Ω分成2个集合：

Ω1={x∈Ω:u(x,t)<1}Ω2={x∈Ω:u(x,t)≥1}

根据Ω2的定义，可以得到:

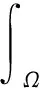
(7)

其中c2>0。由不等式(6)和(7)可得:

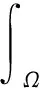
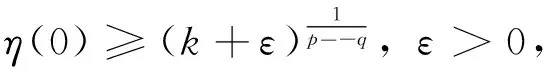
η″(t)≥-λ1η(t)+εηq(t)-c2

当α=η(0)充分大时，应用引理2可得-λ1η(t)+εηq(t)-c2>0，再注意到:

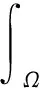
因此:

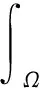
于是定理3得证。

[1]Pao C V.Nonlinear Parabolic and Elliptic Equations[M]. New York：Plenum Press, 1992.

[2] Samarskii A A, Galaktionov V A, Kurdyumov S P，et al. Blow-up in Quasilinear Parabolic Equations[M]. New York:Walter de Gruyter, 1995.

[3] Antontsev S N, Shmarev S I.Existence and uniqueness of solutions of degenerate parabolic equations with variable exponents of nonlinearity[J].J Math Sci, 2008,150:2289-2301.

[4] Antontsev S N, Shmarev S I.A model porous medium equation with variable exponent nonlinearity: existence, uniqueness and localization properties of solutions[J]. Nonlinear Anal,2005,60:515-545.

[5] Pinasco J P.Blow-up for parabolic and hyperbolic problems with variable exponents[J].Nonlinear Anal，2009,71:1094-1099.

[6] Bai Xue-li,Zheng Si-ning. A semilinear parabolic system with coupling variable exponents[J]. Annali di Mathematic Pura ed Application,2011,190 (3): 525-537.

[7] 刘云霞.带有变指标反应项的半线性抛物方程的临界指标[D].大连:大连理工大学,2009.

[8] Glassey R T.Blow-up theorems for nonlinear wave equations[J].Math Z, 1973,132: 183-203.

[编辑] 洪云飞

10.3969/j.issn.1673-1409.2011.12.001

O175.2

A

1673-1409(2011)12-0001-03