基于Merton跳扩散的抵押贷款保险的创新及评价
2011-11-18陈丽萍
陈丽萍
(湖南财政经济学院基础课部,湖南 长沙 410205)
基于Merton跳扩散的抵押贷款保险的创新及评价
陈丽萍
(湖南财政经济学院基础课部,湖南 长沙 410205)
在住房抵押贷款部分担保保证险的基础上进行了创新设计,并假设房价服从Merton跳扩散过程,利用特殊的鞅定价方法,得到了该抵押贷款保险的定价公式。
跳扩散;保险;期权;鞅定价;创新设计
住房抵押贷款这一金融业务现在已经非常普及,数量很大,但其间也存在着巨大的风险。美国次级抵押贷款危机就是一个很好的警示。贷款机构为减少风险,通常要求买房者在申请贷款的同时购买保险[1]。由于风险分析和管理手段的落后,我国住房抵押贷款保险发展较为滞后,并且因地而异。 目前,我国的住房抵押贷款保险主要有3种形式[2]:房屋财产保险、抵押贷款保证保险、住房抵押贷款寿险,其品种单一,保险费用较高,付款方式不够灵活,并且实施的城市很少,远远不能满足我国的实际需要。不同的购房者有不同资信状况和经济实力,多样化的险种有利于银行和购房者做出灵活的决策。因此,有必要推出新的抵押贷款险种,或者在原有险种的基础上进行创新,使之更符合广大购房者的实际情况。
住房抵押贷款保证险是贷款机构要求借款购房者投保的险种,在借款期限内,如果借款人因遭遇意外情况不能如期偿还借款,则由承保人赔付贷款机构的损失。住房抵押贷款保证险包括2种类型:全额担保和部分担保。部分担保指的是保险公司为减少承担的信用风险,只对抵押贷款余额的一定比例实施担保。下面,笔者借鉴国外保险的经验,在部分担保保证险的基础上进行了一定的创新,提出了抵押贷款共同保险的新概念;考虑到重大突发事件对房产价格的影响,引入Merton跳扩散随机过程来模拟房产价格的变动,利用特殊的鞅方法给出了该新保险的评价模型。
1 房屋抵押贷款保险的创新设计
借鉴国外保险经验,基于部分担保保证险,提出了如下抵押贷款共同保险的新概念:若最终的损失额低于保险机构的第一赔付限额k1A0,则由保险公司取得房产权,并向贷款机构支付全部未偿贷款余额,此时,贷款机构所持有的共同保险保单可获得的赔付额为max(UH(T)-αPH(T),0);超过这一赔付限额k1A0的部分,则按照一定的比例k2在保险公司和贷款机构之间分配损失额,不妨称这种保险为房屋抵押贷款共同保险。
贷款机构持有的这种抵押贷款共同保险保单到期收益为:
(1)
式中,A0表示原始贷款本金;UH(T)表示T时刻的未偿付金额;PH(T)表示T时刻的房产价格;α表示保险公司实现房屋抵押权后所得的住房价值比例。
2 数理金融模型的构建
假设市场无套利,所有的随机过程和随机变量都定义在概率空间(Ω,F,P)上,P为风险中性概率测
度,(Ft)0≤t≤T为相应的自然信息流,满足通常条件,Ft=F;到期日用t=T表示,现在时刻用t=0表示,常数r表示无风险利率;UH(t)表示t时刻的未偿付额, 由于它可以通过风险信用评估得到,因此不妨设它为常数UH;房产价格PH(t)是一个随机变量,满足如下随机微分方程:
(2)
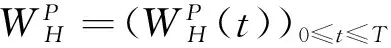

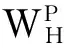
(3)
3 基于Merton跳扩散的抵押贷款保险的特殊鞅评价
目前,无套利定价理论是未定权益定价理论中最为突出的,比偏微分方程式简单,且不会涉及复杂的积分。简单的讲,无套利定价理论的基本前提就是假设市场无套利,即存在鞅测度(即风险中性概率测度)。 更深一层的讲,若市场是完备的,则鞅测度存在且唯一,该完备市场中的任何未定权益都有唯一的无套利价格;若市场是不完备的,则存在许多的鞅测度,此时,对不可复制的未定权益,就无法得到唯一的无套利价格。 实证结果表明,金融市场通常是有套利的,不完备的。而对于这样的市场,等价鞅测度可能不存在,用无套利定价方法就有一定的困难。显然,此处的市场模型是不完备的,因此风险中性概率测度不唯一,要得到与投资者的风险态度无关的唯一定价是不可能的。但是,公平的价格一定等于某个等价鞅测度所确定的风险中性定价,因此,结合投资者的风险态度,从所有等价鞅测度中选择一个恰当的鞅测度就是问题的关键。
由Girsanov定理,定义:
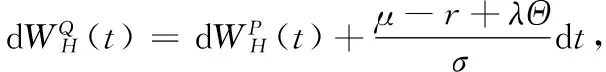
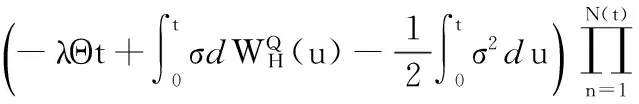
(4)
易知,在概率测度Q下,房产的贴现价格过程YH是鞅。
引理1[3]设φ(·)为标准正态分布的密度函数,σ(R(u);0≤u≤T)为过程R生成的σ-代数,则:

为简便起见,不妨定义集合:
B={UH(T)>αPH(T),UH(T)-αPH(T) 根据未定权益的鞅定价方法[4],抵押贷款共同保险保单在现在时刻的价值为: 式中,EQ(·)代表测度Q下的期望值;IB代表集合B的示性函数。 将上式中的第1、2、3、4项分别记为I1、I2、I3和I4,下面化简集合B和C: 类似地计算化简,得: 根据式(4)及引理1, 得: EQ[YH(T)IB|σ(R(u),0≤u≤T)] I2=-αEQ[YH(T)IB] 类似地计算得: 综上,最后得到如下结论。 定理1设房屋抵押贷款共同保险保单到期收益满足式(1),无风险利率为常数r,未偿付额UH(T()恒为常数UH,房产价格PH(t)满足式(2),则创新的抵押贷款共同保险的特殊鞅定价公式(即保费计算公式)为: 注:定理1中的保费计算公式与参数μ的取值无关。 [1] 侯新华,田策.住房抵押贷款保证险研究[J].中国房地产金融,2002(11):11-13. [2] 钱乃余.发展我国住房抵押贷款保险之构想[J].济南金融,2001(6),37-38. [3] 李晨,陈丽萍, 杨向群. 随机波动率与跳扩散相结合的保证险的鞅定价[J].系统工程,2009,27(3):41-45. [4] 沈明轩,杜雪樵.跳-扩散幂型支付的期权定价公式[J]. 数学的实践与认识,2009,39(6):33-37. [编辑] 洪云飞 10.3969/j.issn.1673-1409.2011.08.001 O211.6;F830.9 A 1673-1409(2011)08-0001-03



