改进了系统差附加条件的半参数回归与模型精化

郑 磊,陈宏玉,张启斌,史永江

(1.天津市市政工程设计研究院,天津 300051;2.江苏省工程物理勘察院,江苏 南京 210008)

改进了系统差附加条件的半参数回归与模型精化

郑 磊1,陈宏玉2,张启斌1,史永江1

(1.天津市市政工程设计研究院,天津 300051;2.江苏省工程物理勘察院,江苏 南京 210008)

系统差之和 ∑si≠0时,利用附加系统差之和 ∑si=0的半参数模型往往得不到较好的数据处理结果,文中从理论上对系统差附加条件进行了改进,并基于改进前、改进后的半参数模型以及经典最小二乘平差模型对系统差之和 ∑si≠0时的算例进行处理。结果表明,改进后的半参数模型大大提高了数据处理精度。

系统差;半参数回归;模型精化

半参数回归模型是20世纪80年代统计学界为了处理系统偏差而提出来的,它主要是将信号视为非随机参数,采用补偿最小二乘法,得到参数与信号的估值。Fischer[1-2]、Hansen[3-4]、孙海燕[5]、丁士俊[6]、王振杰[7]等国内外学者对半参数模型、正则矩阵R的选取、平滑因子的确定等问题进行了研究并给出了一些有益的结论。其中,孙海燕等在系统差之和满足 ∑si=0的条件下,推导了相应的半参数模型计算公式[6];刘忠等在正则矩阵为 R=GTG、系统差之和满足 ∑si=0的条件下对GPS绝对定位中的系统偏差进行了分离研究[8]。但是,关于电离层延迟、对流层延迟等系统差条件的半参数回归与模型精化的研究还很少。为此,文中在选取正则矩阵 R=GTG,利用L-曲线法确定平滑因子的前提下,对系统差之和 ∑si≠0条件下的半参数回归进行了理论上的推导,并对改正后模型的数据处理效果进行了验证。

1 平差模型与解算方法

半参数模型、误差方程、估计准则分别为

式中:L为n维观测向量;X为t维参数向量;B为列满秩设计矩阵;Δ为n维观测误差向量;V为n维残差向量;S为描述模型误差或系统误差的n维向量;P为对称正定方阵,观测值L的权;R为正则矩阵;α为平滑因子。

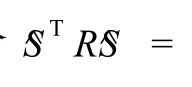
由于rank(R)=n-1＜n,即 R秩亏,还需再增加一个约束条件。本文将系统差之和表示为

式中:n为数据个数;C为系统差均值(C=0只是其中的一个特例)。

平滑因子α可以通过L-曲线法确定[7],这里不再过多介绍。

这样就把平差问题归结为一个条件极值问题,由拉格朗日乘数法,构造函数

2 算例分析

构造一个模拟的平差问题,分别利用经典最小二乘法、改进前半参数模型、改进后半参数模型进行平差求解,以更好地说明改正后的半参数平差模型的数据处理效果。

假设有线性模型 Y1=B X,并取 X=[3,3]T。B(bi,j)为100×2阶矩阵,ti=2＊pi＊(i-1)/100,i=1,2,3,…,n;bi,1=ti;bi,2=(ti/2)2;K=3为系统误差均值,系统误差 Y2=[y1y2…… y100],yi=K+5sin(2＊ti);观测值的真值 L^=Y1+Y2;观测误差Δ是由100个服从 N(0,1)分布的正态随机数组成的列向量;观测值L=Y1+Y2+Δ。

由于系统差之和 ∑si=0,只是本文平差模型的一个特例,因此,可以将系统差均值 C分别设置为0和3,利用上述平差公式分别进行平差,即可对本文改进后的半参数模型数据处理效果进行验证。

经典最小二乘法参数平差结果(X jd)、∑si=0时的半参数模型参数平差结果(Xbc0)、∑si=100＊3时的半参数模型参数平差结果(Xbc1)与参数真值(X)如表格1所示。从表格1给出的数据可以看出,在系统误差相对偶然误差较大时,经典最小二乘平差法得到的参数结果严重偏离了真值,证明半参数平差模型有效性;但是,当系统差 ∑si≠0时,如果还按照 ∑si=0附加条件的半参数模型平差,那么,参数平差结果也将与参数真值出现较大的偏差;而按照本文给出的系统差附加 ∑si=100＊3的半参数模型进行平差则得到了较好的结果。表格1的数据表明,本文给出的半参数数据处理模型对于系统均值不为0时的情况具有很好的处理效果。

表1 3种方案计算的 X估值的比较

系统差真值(s)、∑si=0时的半参数模型系统差估值(sbc0)、∑si=100＊3时的半参数模型系统差估值(sbc1)的对比曲线如图1所示。从图1可以看出,利用 ∑si=0时的半参数模型解算得到的系统差估值明显偏离了系统差真值,而且这种偏离具有斜向下逐步增大的趋势;而利用 ∑si=100＊3时的半参数模型解算得到的系统差估值则与系统差真值具有良好的一致性。图1系统差对比曲线表明,充分考虑系统差均值不为0之后的半参数模型的系统差分离效果得到了很大提高。

图1 两种方案计算的信号估值与信号真值的比较

观测值(Lobj)、经典最小二乘法拟合观测值(L jd)、∑si=0时的半参数模型拟合观测值(Lbc0)、∑si=100＊3时的半参数模型拟合观测值(Lbc1)的对比曲线如图2所示。从图2可以看出,L jd曲线近似一条直线且均匀分布在观测值的中间。L jd曲线的这种特点可能主要与经典最小二乘法模型本身即为线性模型且残差平方和最小有关。Lbc0曲线与Lobj曲线存在明显的偏离,且这种偏离是逐步扩大的;而Lbc1曲线则与Lobj曲线具有很好地一致性。Lbc0曲线的这种现象进一步说明在 ∑si≠0时,如果还按照 ∑si=0时的半参数模型进行平差,那么,拟合观测值将存在较大的模型误差。

图2 3种方案计算的观测值估值与观测值真值的比较

经典最小二乘法观测值残差(V jd)、∑si=0时的半参数模型观测值残差(Vbc0)、∑si=100＊3时的半参数模型观测值残差(Vbc1)的对比曲线如图3所示。V jd、Vbc0、Vbc1曲线变化趋势从残差方面进一步验证了本文改进系统差附加条件后半参数模型数据处理效果的有效性。

图3 3种方案计算的观测值残差的比较

3 结束语

本文从理论上对半参数模型系统差附加条件进行了改进和公式推导,通过模拟算例验证了改进后半参数模型数据处理的有效性,并在一定程度上拓宽了该模型数据处理的有效范围。

然而,本文给出的只是模拟算例的数据处理结果。如何将本文给出的模型用在消除诸如电离层、对流层延迟等实际问题当中以及在实际数据处理过程中如何精确确定诸如电离层、对流层等系统差均值等问题还需要进一步的研究和探讨。

[1]FISCHER B.Collocation,Filtering and Nonparametric Regression(Part I).ZfV,1999,1(1):17-24.

[2]FISCHER B.Collocation,Filtering and Nonparametric Regression(Part II).ZfV,1999,1(2):46-52.

[3]HANSEN PC.Analysis of Distance Ill-posed Prolem s by meansof the L-curve.SIAM Rev.,1992,34(4):561-580.

[4]HANSEN PC,O’LEARY D P.The Use of the Lcurve in the Regularization of Discrete Ill-posed Prolems.SIAM J.Sci.Comp.,1993,14(6):1487-1503.

[5]孙海燕,吴云.半参数回归与模型精化[J].武汉大学学报:自然科学版,2002,27(2):172-174.

[6]丁士俊,陶本藻.自然样条半参数模型与系统误差估计[J].武汉大学学报:自然科学版,2004,29(11):964-967.

[7]王振杰,欧吉坤.用L-曲线法确定半参数模型中的平滑因子[J].武汉大学学报:自然科学版,2004,29(7):651-652.

[8]刘忠,瞿伟.利用半参数模型精化 GPS绝对定位中残余的系统偏差[J].测绘工程,2007,16(5):28-30

Sem i-parametric regression and model refin ing using modified additional conditions of systematic error

ZHENG Lei1,CHEN Hong-yu2,ZHANG Qi-bin1,SH I Yong-jiang1
(1.Tianjin M unicipal Engineering Design&Research Institute,Tianjin 300051,China;2.Engineering Geophysical Exploration Institute of Jiangsu Provience,Nanjing 210008,China)

The accuracy of the estimated value of the parameters acquired using semi-parametric model w ith the additional condition of the sum of the estimated value of systematic error∑si≠0,w hile the sum of the estimated value of systematic error∑si=0 in fact,was always not good.So the additional condition of the sum of the estimated value of systematic erro r w asmodified theo retically in this paper and the effective of themodified modelw as p roved using the data w hich the sum of the estimated value of systematic error∑si≠0.The result of the data p rocessed show s that the accuracy of the estimated value of the parameters was imp roved effectively.

systematic error;semi-parametric regression;model refine

P228

A

1006-7949(2011)02-0015-03

2010-07-28

国家863计划资助项目(2009AA 12Z301)

郑 磊(1983-),男,硕士研究生.

[责任编辑张德福]