基于神经网络的DEM趋势面逼近与分析

陈再辉,江丽钧,徐洪波,吴 刚

(丽水市建设局城建测量队,浙江 丽水 323000)

基于神经网络的DEM趋势面逼近与分析

陈再辉,江丽钧,徐洪波,吴 刚

(丽水市建设局城建测量队,浙江 丽水 323000)

趋势面从宏观上揭示研究对象的特性,在各领域发挥着重要作用。神经网络可以对复杂系统进行无限逼近,进而进行预测。基于贝叶斯正则化BP神经网络和RBF神经网络对DEM趋势面进行逼近,并与二次多项式建立的DEM趋势面进行比较分析,证明该方法的可行性和有效性。

BP神经网络;RBF神经网络;DEM;趋势面

趋势面从宏观上揭示了在二维空间上连续变化的地物特征。趋势面在各领域有着重要的作用,文献[1]采用趋势面对水深数据进行了分析,识别水深测量中的水深误差。文献[2-3]建立了地价趋势模型,对城市基准地价进行了分析,采用移动趋势面分析法测算城市基准地价。文献[4]采用趋势面建立了地面沉降模型,对地面沉降进行了分析。文献[5]采用趋势面建立了已知站点降雨量逼近模型,对降雨量的变化趋势进行了研究。此外趋势面还可以用于电磁辐射、海洋重力场和气温等领域的进一步研究。

多项式是建立趋势面的常用方法,多项式次数较低时,对地形的描述不够详细;多项式次数较高时,对地形的模拟又会产生突变,同时误差的传播也比较快。神经网络可以对复杂系统进行无限逼近,并在此基础上进行有效的预测。本文使用贝叶斯正则化BP神经网络和RBF神经网络对DEM趋势面进行逼近,并与二次多项式建立的DEM趋势面进行比较分析。

1 方法介绍

1.1 二次多项式拟合DEM趋势面

趋势面拟合多采用多项式,其中二次多项式是最为常用的一种,方程为

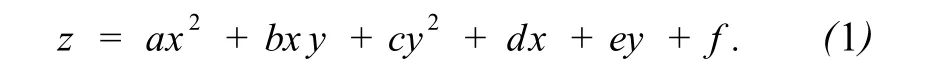
误差方程式可表示为

其中方程式系数矩阵

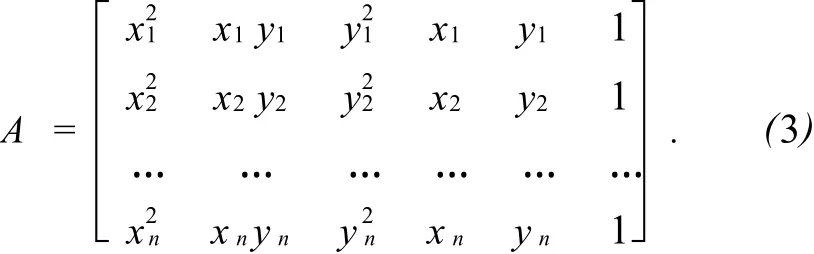
X和L分别为参数矩阵和高程观测值矩阵,分别表示为

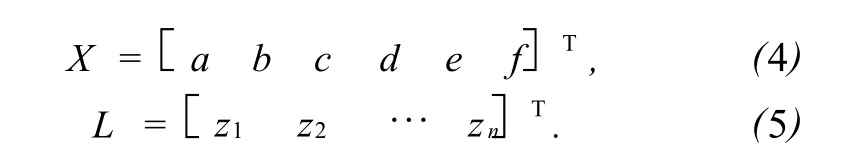
根据参数平差原理解算,可得

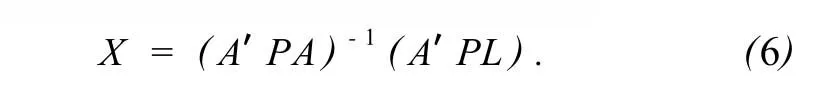
1.2 B P神经网络逼近D EM趋势面

1.2.1 BP神经网络原理

BP神经网络包括输入层、中间层和输出层。上下层之间全连接,每层神经元之间无连接。网络通过学习样本激活神经元从输入层经中间层向输出层传播,输出层各神经元得到网络的输入响应。接着按照减小目标输出与实际输出之间误差的方向,从输出层经中间层回到输入层。

常用的传递函数有Sigmoid型的对数、正切和线性函数。传递函数处处可微,是一个非线性超平面组成的区域,分类比较精细,容错性比较好[6]。采用梯度下降法学习,权值修正解析式十分明确,学习效率比较高。

输入层与中间层的传输公式为

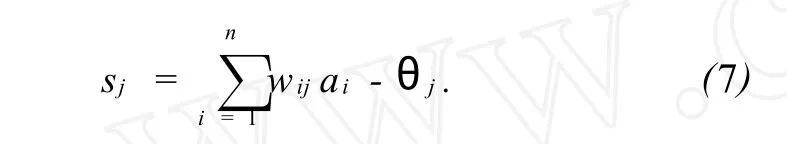
式中:sj为中间层各单元的输入,wij和θj分别为连接权和阈值。

式中:bj为中间层通过输入层与中间层的传递函数以后各单元的输出。

中间层与输出层的传输公式为

式中:st为输出层各单元的输出,vjt和γt分别为连接权和阈值。

bt=g(st). (10)

式中:bt为通过中间层与输出层的传递函数以后各单元的输出。

关于BP神经网络的学习过程和公式推导文献[6]中有详细阐述。

1.2.2 贝叶斯正则化

贝叶斯正则化是利用贝叶斯的统计方法自动决定正则化参数。网络训练误差函数为

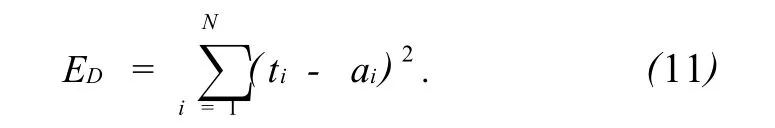
式中:ti为实际输出,ai为期望输出,网络权重平方和为

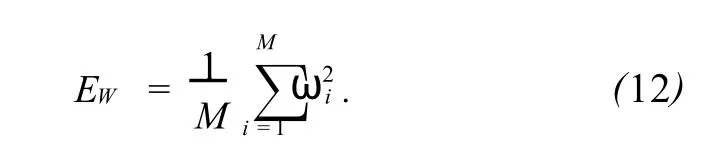
其中ωi是神经网络连接权,网络性能函数为

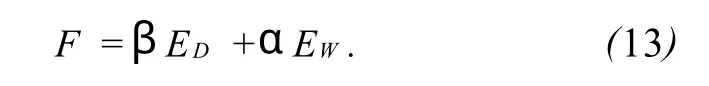
贝叶斯正则化方法在训练过程中自动调节超参数α和β的大小,使其达到最优。有关贝叶斯正则化方法的详细叙述参见文献[7-10]。

1.3 RB F神经网络逼近D EM趋势面

1.3.1 RBF神经网络原理

RBF神经网络是由输入层、隐含层和输出层构成的三层前向网络,隐含层采用径向基函数作为激励函数。隐含层每个神经元与输入层相连的权值向量和输入矢量之间的距离乘以阈值作为输入,输入层与中间层的传输公式为

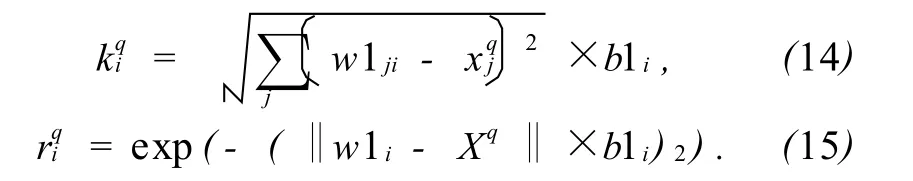
式中:kqi和rqi分别是中间层各单元的输入和输出,w1ji和b1i分别是连接权和阈值。

中间层与输出层的传输公式为

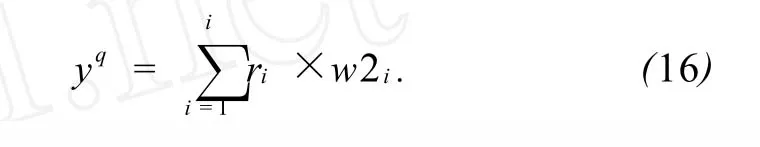
式中:yq是输出层各单元的输出,ri和w 2i分别是输入和连接权。

公众号粉丝数量多且覆盖范围广，影响力大。便于公众号整合行业内资源，使信息传达更加便捷，集中管理更加容易。

1.3.2 SPREAD参数的确定

SPREAD为径向基函数的分布密度,SPREAD值越大,函数越平滑。RBF神经网络的关键在于SPREAD参数的确定。网络的建立过程就是训练过程,实际上就是SPREAD参数的确定过程。给定参数区间,绘制训练的误差曲线,观察曲线确定参数的取值区间,在区间内再进行训练并观察误差曲线,直到参数的取值能够满足需要的精度。

2 实例分析

分别使用常规二次多项式、贝叶斯正则化BP神经网络和RBF神经网络3种方法建立DEM趋势面。使用均匀分布在420 m×420 m范围内的441个格网点进行趋势面逼近,高程位于1 450 m到1 550 m之间。将441个点分为两组,第1组401个,作为训练数据,第2组40个,作为检验数据。

2.1 BP神经网络逼近DEM趋势面过程

设计3层的网络结构,输入单元数为2个,输出单元数1个,通过训练过程绘制训练误差与隐含层单元数的关系图,如图1所示。从图1中可以看出,中间单元数为23个时训练误差最小,所以隐含单元数确定为23个。

BP神经网络逼近DEM趋势面时,将 x和y坐标作为输入向量,z坐标作为目标向量,对设计的网络进行训练,然后用训练好的网络对新的输入向量进行预测,并分析预测结果。

计算步骤:

图1 网络训练误差

（犔犲狏犲狀犺犲狉犵2犕犪狉狇狌犪狉犱狋）算法。

2)对训练数据的输入向量和目标向量进行归一化。

数据归一化采用线性转换函数,公式为

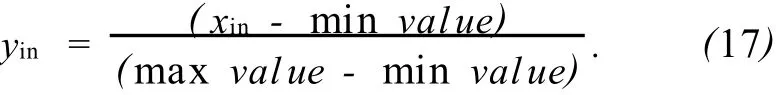
式中:x和y分别为转换前后的值。

3)将归一化的数据提供给设计好的网络进行训练。

4)将结果进行反归一化输出,公式为

5)将第2组检测数据作为输入向量,用上面训练好的网络模式对输入向量的目标向量进行预测,用实际值和预测值进行比较,检验网络的精度。

2.2 RBF神经网络逼近DEM趋势面过程

设计3层的网络结构,输入单元数为2个,输出单元数1个。通过训练绘制预报误差曲线如图2所示,通过观察,确定 SPREAD=3.5。

图2 网络预报误差

2.3 结果与分析

二次多项式、贝叶斯正则化BP神经网络和RBF神经网络的拟合残差分别如图3、图4和图5所示,3种方法的检验残差分别如图6、图7和图8所示,拟合精度和检验精度如表1所示。

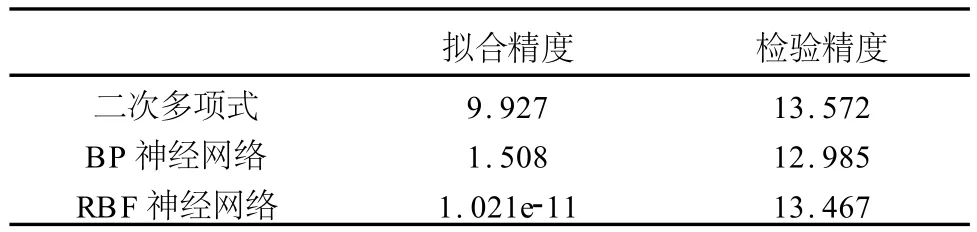
表1 拟合和检验统计表

?

从图3和图4可以看出神经网络的拟合残差比二次多项式的拟合残差小得多,BP神经网络的拟合残差基本上小于6 m,RBF神经网络的拟合残差基本上小于0.1 m,拟合效果最好。从图3～图8可以看出对于大部分格网点,神经网络的检测残差比二次多项式的检测残差要小,图中残差比较大的点是位于测区边缘的高程点,其中BP神经网络的检验精度最高。从表1可以看出神经网络的拟合精度和检验精度都比二次多项式要小,这两种方法可以用于DEM趋势面拟合。

3 结 论

1)使用贝叶斯正则化自动调整超参数,逼近DEM趋势面的泛化效果比较好。

2)基于神经网络建立的DEM趋势面,也可用于对最小二乘配置法中的趋势部分进行有效逼近,从而提高最小二乘配置法建立DEM的精度。

3)针对BP神经网络会陷入局部极小值的问题,可考虑采用粒子群理论对其进行改正,以达到全局最优。

4)对于 RBF神经网络中参数 SPREAD的确定,通过训练并绘制训练的误差曲线,不断缩小测试区间进行训练,确定参数的取值。

[1]胡光海,周兴华.趋势面分析在水深测量数据处理中的应用[J].测绘工程,2004,13(3):25-27.

[2]焦利民,刘耀林,叶宗达.基于神经网络趋势面分析的地价样点检验方法研究[J].测绘信息与工程,2007,32(6):29-31.

[3]段滔,刘耀林.基于移动趋势面分析法的城市基准地价评估研究[J].武汉大学学报:信息科学版,2004,29(6):529-532.

[4]高玉山.济宁市地面沉降的趋势面分析[J].济宁学院学报,2007,28(6):33-35.

[5]张渭军,王文科,孔金玲,等.基于移动趋势面的降水面雨量分析[J].水土保持研究,2006,13(2):99-101.

[7]李旭军.贝叶斯正则化的BP神经网络在经济预测中的应用[J].科技信息,2008(4):67-69.

[8]葛哲学,孙志强.神经网络理论与MATLAB R2007实现[M].北京:电子工业出版社,2007.

[9]缪宁,邓小珍,刘文远,等.基于贝叶斯正则化神经网络虚拟企业敏捷性评价[J].计算机工程与应用,2008,44(8):223-225.

[10]MACKA Y,D.J.C.Bayesian interpolation[J],Neural Computation.1992,4(3):415-447.

[11]FORESEE FD,HAGAN FD.Gauss-New ton App roximation to Bayesian Regularization[A].Proceeding of the IEEE International Joint Conference on Neural Netwo rks[C].1997(6):1930-1935.

Approximation and analysis of DEM trend based on neutral network

CHEN Zai-hui,JIANG Li-jun,XU Hong-bo,WU Gang
(Surveying Union of City Construction,Bureau of Construction in Lishui,Lishui 323000,China)

Trend can open out the characteristic of research object,and exert important effect in many domains.BP neutral network can app roach comp lex system infinitum,and p rocess forecast.In the paper,DEM trend based on Bayesian Regularization BP neutral network and RBF neural network is constructed.Compared w ith DEM trend using quadratic polynom ial,the feasibility and validity are p roved.

BP neutral netwo rk;RBF neutral netwo rk;DEM;trend

TP183

A

1006-7949(2011)02-0066-04

2010-03-14

陈再辉(1981-),女,工程师,硕士.

[责任编辑刘文霞]