滚动轴承的实调制细化包络谱诊断方法研究

黄国樑，周玉彬，郭 华，时献江

（1.哈尔滨大东人造板设备制造有限公司，黑龙江 哈尔滨 150040；2.哈尔滨理工大学机械动力工程学院，黑龙江 哈尔滨 150080）

0 引 言

滚动轴承的振动信号往往具有调制信号特征，此时，轴承的部件共振频率成分为信号的载波频率，故障频率为调制频率。通常载波信号频率较高，且远离一般零部件的故障振动频率范围，可以利用高频段提取轴承的故障信息，避开低频段其他振动能量较大信号的干扰，这就是常见的滚动轴承故障诊断的共振解调法。

共振解调法的主要思想是去掉信号中无用的部件共振频率成分，仅提取有用的调制故障频率成分，这可以用Hilbert变换求包络谱的方法来实现。但是，由于轴承部件本身的共振频率较高，通常需要采用较高的采样频率，因此直接对原始信号进行包络分析往往会由于频谱的分辨率过低而无法识别故障特征。为此，很多学者提出了细化包络谱的概念，常见的有采用Hilbert变换+细化谱实现的数字细化包络方法[1-3]，采用小波变换的细化包络算法等[4]。该文根据通信信号中的调制与解调原理，参照复调制细化谱的复调制移频原理，并利用Hilbert变换求包络谱技术，实现了一种实数调制+Hilbert变换求包络的新细化包络谱算法，并在Matlab环境下实现，最后给出了该算法在滚动轴承故障诊断中的应用。

1 复调制移频原理

采用复调制的移频过程如图1所示。其基本原理是先将感兴趣的某一高频频段平移至低频段，这相当于对原始信号x（t）进行复调制，即

式中：f0——欲细化频段的中心频率。

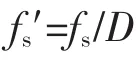
2 实调制移频算法原理

时域离散化会引起信号频谱的周期性变化，即一个待分析的频段应是一个正负频率对称的，采用复调制法的结果却会破坏这种对称结构（如图1所示）。当欲细化分析频段的中心频率为f0，宽度为B时，可以采用图2所示的移频过程，即正频率部分左移f0-B/2，负频率部分右移f0-B/2，这个移动过程在频域的数学表达式为

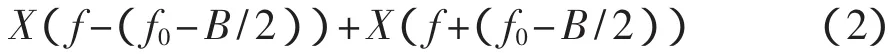
其在时域中的表达式为

也就是说，对原始信号x（t）乘以2cos（2π（f0-B/2）t）就可以实现图2所示的移频过程，相对于复调制，称为实调制，其移频计算流程如图3所示。由于实调制后的信号频谱保持了原来的正负频率成分对称关系，所以调制结果仍为实信号，这为后续采用Hilbert变换求包络谱提供了可能。

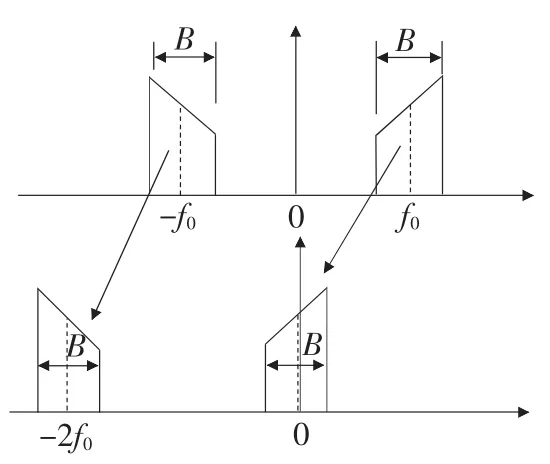
图1 复调制方式下的移频过程示意图

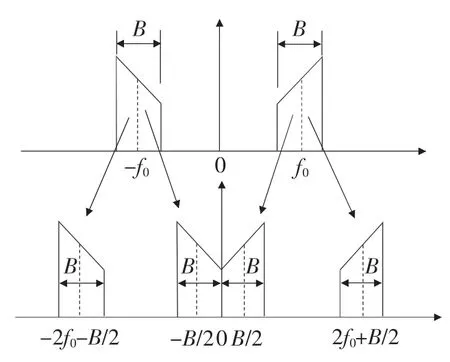
图2 实调制方式下的移频过程示意图

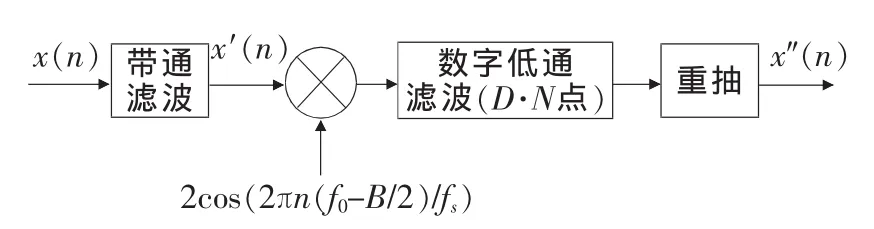
图3 实调制移频算法流程图

3 Hilbert变换及包络谱算法

3.1 基本原理

设x（t）为一个实时域信号，其Hilbert变换定义为

则原始信号 x（t）和它的 Hilbert变换信号 h（t）可以构成一个新的解析信号xa（t）

其幅值

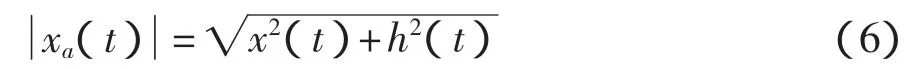
便为原始信号x（t）的幅值解调信号[6]。

根据傅里叶变换原理，信号x（t）的Hilbert变换在频域中的表达式为

可见，Hilbert变换相当于一个幅频特性为1的全通滤波器，信号x（t）通过Hilbert变换后，幅值不变，仅仅是负频率做了+90°相移，正频率做了-90°相移。

3.2 采用Hilbert变换的信号解调计算流程

（1）将待分析信号x（n）通过傅里叶变换得到它的频域函数X（k）。

（2）根据式（7），将正频率相移-90°，负频率相移90°，得到经过相移的频域函数X′（k）。

（3）对X′（k）进行傅里叶逆变换得到时域信号x′（n），它即是x（n）的Hilbert变换h（n）。

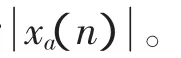
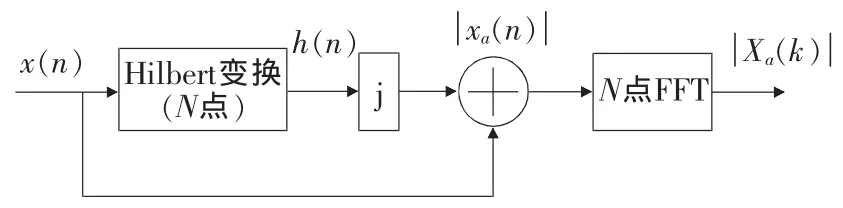
图4 采用Hilbert变换的包络谱算法流程图

4 实调制细化包络谱求解方法

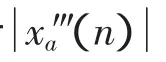
图5 实调制细化包络谱算法流程图

根据3.2知，采用Hilbert求包络谱过程需要进行3次FFT运算，计算量较大。实调制移频方法是将Hilbert变换求包络谱过程放在了实调制和重新采样之后，这样，Hilbert变换过程仅针对重抽后的N点信号进行计算，而不是原始的D·N点信号，所以计算量大大减少，提高了细化包络谱的计算速度。这是和其他细化包络谱求解方法的显著区别点之一。

5 实调制细化包络谱在滚动故障诊断中应用

将该方法应用在滚动轴承故障诊断中，进行了滚动轴承故障诊断的实验验证。实验选用308轴承，通过在轴承外圈滚道上人工钻坑模拟滚动轴承的外圈故障，采用加速度传感器测取轴承的径向振动信号。试验时轴承转速为1000r/min，信号采样频率为20 kHz，基本采样点数N=1 024，细化分析时采样点数为5 120，细化倍数D=5，采样时模拟抗混滤波器的截止频率为3kHz，包络分析时带通滤波器的带通范围为4~10 kHz。分别应用普通分辨率的FFT频谱、Hilbert包络谱及实调制细化包络算法对实验结果进行了分析与比较。

图6为轴承外圈故障时的振动加速度时域波形，图7为带通滤波后的普通分辨率幅值谱，可见在7kHz左右有一个共振峰，且有明显的等频率间隔的边带成分。由于频谱分辨率较低，难于精确地识别边带成份。

图6 外圈故障时的振动加速度时域波形

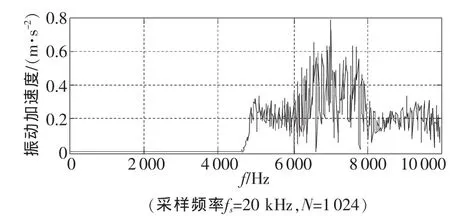
图7 带通滤波后的原始信号频谱

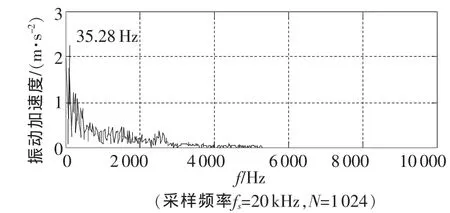
图8 外圈故障时的普通分辨率Hilbert包络谱

图8为轴承外圈故障，采样点数N=1 024时的Hilbert变换包络谱。可见，由于频率分辨率较低，解调后故障特征频率信号均集中于低频处，谱图中实际计算的故障特征频率为35.28 Hz，与理论计算故障频率49.23Hz（308轴承，转速为 1000r/min）相差较大。图9为细化倍数D=5时的实调制细化包络谱，已经可以清晰地分辨出滚动轴承外圈故障的特征频率（实测为47.38 Hz）及其倍频，而且与理论计算值非常接近。另外，与图8比较，图9中除故障特征频率外，其他干扰成分也大大减少，主要原因在于调制移频过程实际上又相当增加了一次共振解调过程。即用一个和部件共振频率成分接近的信号与原始信号相乘，会由于共振作用放大共振频率及其调制的故障特征频率，压缩其他无关的频率成分，能够提高信号分析的信噪比，这也是实调制移频细化谱应用于滚动轴承故障诊断的优点之一。

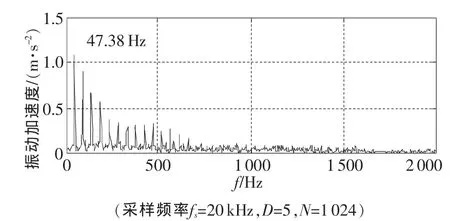
图9 外圈故障时的实调制细化包络谱

6 结束语

采用实调制频移技术结合Hilbert变换，可以使细化包络谱的计算效率大大提高，而且由于实调制过程本身的二次共振解调作用，还可以放大部件的共振频率及其调制的故障频率成分，压缩其他无关的频率成分，提高信号分析的信噪比。

在滚动轴承的细化包络谱中，由于将2个边带（故障频率）合为一根谱线，有信息凝合的作用，克服了原始信号频谱中边带不对称问题。由于能够剔除无用的部件共振频率成分，得到的细化包络谱能更精细、准确地反映故障特征频率的变化，说明该方法具有实际应用价值。

[1]何景光，吴雅，皮钧，等.一种包络谱细化的新方法及其在故障诊断中的应用[J].华中理工大学学报，1993，21（1）：95-99.

[2]皮钧，王建军.包络谱细化的新方法及其在齿轮故障诊断中的应用[J].拖拉机与农用运输车，2003（5）：10-12.

[3]杜秋华，杨曙年.细化包络分析在滚动轴承缺陷诊断中的应用[J].轴承，2004（3）：31-34.

[4]万书亭，吕路勇.基于小波包和细化包络分析的滚动轴承故障诊断方法研究[J].中国工程机械学报，2008，6（3）：349-353.