经纬仪交会测量系统的图形结构评价
2011-11-14王耀华陈继华
王耀华,陈继华
(1.信息工程大学测绘学院,河南郑州450052;2.北京航空航天大学仪器与光电工程学院,北京100083)
或表示为
经纬仪交会测量系统的图形结构评价
王耀华1,陈继华2
(1.信息工程大学测绘学院,河南郑州450052;2.北京航空航天大学仪器与光电工程学院,北京100083)
以两台或多台电子经纬仪为主的交会测量系统是进行工业产品尺寸检测的重要系统设备之一,但其测量精度会受到环境条件、仪器精度、测站与被测对象的空间分布状况等的影响,尤其是测站与待测点形成的交会图形结构是影响其精度的重要因素。提出采用图形结构衰减因子(GDOP)来评价交会图形结构优劣,给出GDOP的计算方法及空间分布。通过仿真分析及对比测试表明,GDOP的大小能有效地反映交会测点的误差大小,并能通过GDOP量化评价图形结构的优劣。
工业测量;GDOP;空间前方交会;经纬仪
经纬仪交会测量系统以空间前方交会原理[1]为基础,首先通过两台经纬仪互瞄及测量基准尺,采用相应的系统标定算法[2-4]获取两测站的坐标及方位;然后将两台仪器同时瞄准待测点测角,通过交会解算目标点的空间三维坐标[5]。经纬仪交会测量系统主要用于大型工业产品、部件以及生产、实验设备的空间大尺寸几何测量或安装调试[6-8]。其检测精度受检测环境条件、仪器的精度等级、被检测产品的尺寸大小、仪器与被检对象的空间分布状况等多种因素的影响。这些因素中部分可以人为控制,对这些可控制因素的影响,须采取一定的措施进行改善或限制。如交会图形结构会对测量精度产生较大影响,则可以选择合理的设站方式及测点分布保证良好的交会图形[9-10]。
针对交会图形结构优劣的评价,许多文献采用空间交会角的方式[5,11],但分析研究表明,交会角与测点误差并不具备一致的规律,不能完全准确地代表交会图形,不便对交会图形结构进行量化评价。借鉴GPS对交会图形的评价方法[12-14],本文提出一种称为“几何图形衰减因子”的量,来定量评价交会图形结构。仿真分析及对比测试表明,GDOP与交会测点误差具有明显的规律,能有效地反映交会测点的误差大小。
一、交会图形结构对测点误差的影响
当采用由两台电子经纬仪构成的测量系统对空间点进行交会测量时,两测站对点观测形成的空间直线相交而成的角度称为交会角;两个测站点与待测点形成的空间三角形称为交会图形。由于交会图形的不同,相同的观测值误差会导致点坐标具有不同的测量误差,如图1所示。图中,Δα为角度测量真误差;ΔP为角度测量误差引起的实际点位真误差;1、2两点表示两个交会测站。
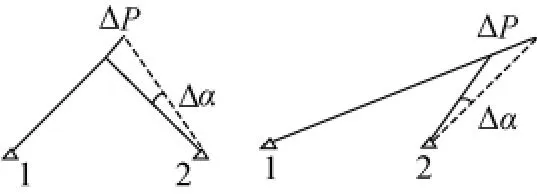
图1 交会图形对测点误差的影响
由图1可知,交会图形结构不同,测点误差有很大差异。显然,当交会角接近于90°时观测值误差引起的测点误差小;同时,待测点距离测站的远近也会引起不同的测点误差。以下针对两台经纬仪的观测角进行前方交会,并采用GDOP来评价空间交会图形结构。
二、GDOP的定义及计算
两站角度交会时,由于存在角度观测误差,使得空间交会点位于如图2所示的两个圆锥相交的空间区域内。图2中,S1为测站1到标定点的距离;S2为测站2到标定点的距离;S为两测站间距离;γ为交会角;α1为测站1到标定点的空间直线与两测站连线的空间夹角,α2与 α1含义类似;在交会测点时,Δα为每站角度测量真误差上限。

图2 两站角度交会的交会区域
将图2中两个空间圆锥相交的区域投影到测站1、2及交会点形成的交会平面上,如图3所示。

图3 交会点空间分布区域在平面上的投影
该投影区域可以近似为一个平行四边形,其中

显然,两个圆锥相交的空间区域越大,投影区域越大,交会测点的误差也越大。投影区域面积的大小直接决定测点误差的大小,这里取投影区域面积之平方根作为点位误差的等效评价指标,称为等效点位误差,用A表示
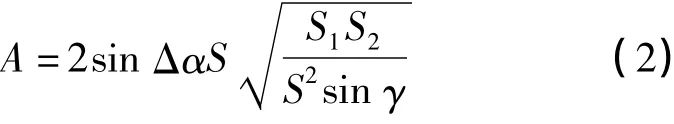
从式(2)可以看出,待测点的点位误差与角度观测误差、两测站间的距离、待测点到两测站间的距离、交会角等有关,其中A与两测站间距离成正比。当设站方式及角度观测误差一定时,A只与有关,将其定义为图形结构衰减因子,经变换后表达为
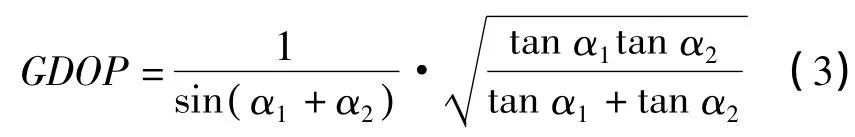
或表示为

式中,γ=π-α1-α2。由式(3)可知GDOP只与α1、α2有关,图2所示的空间交会三角形的图形结构可由α1、α2唯一确定,因此GDOP可综合代表交会图形结构。此时有

对于两站角度交会,当观测误差及设站方式一定时,等效点位误差A与GDOP呈线性关系,因此GDOP可作为评价测点误差大小的一个基本参数。GDOP中包含了交会角及点位的空间分布状况,从式(4)看出,交会角γ接近90°时,GDOP相对较小,因此,交会角越接近90°,图形结构越好[1,5,11]。
图4绘制出了GDOP与交会角γ间的关系。从图4中可以看出,GDOP与交会角γ间的关系在趋势上出现了多个分支,表明交会角与GDOP没有严格的规律趋势。但总的来说,交会角等于或接近于90°时,GDOP较小;交会角小于30°时,GDOP较大。
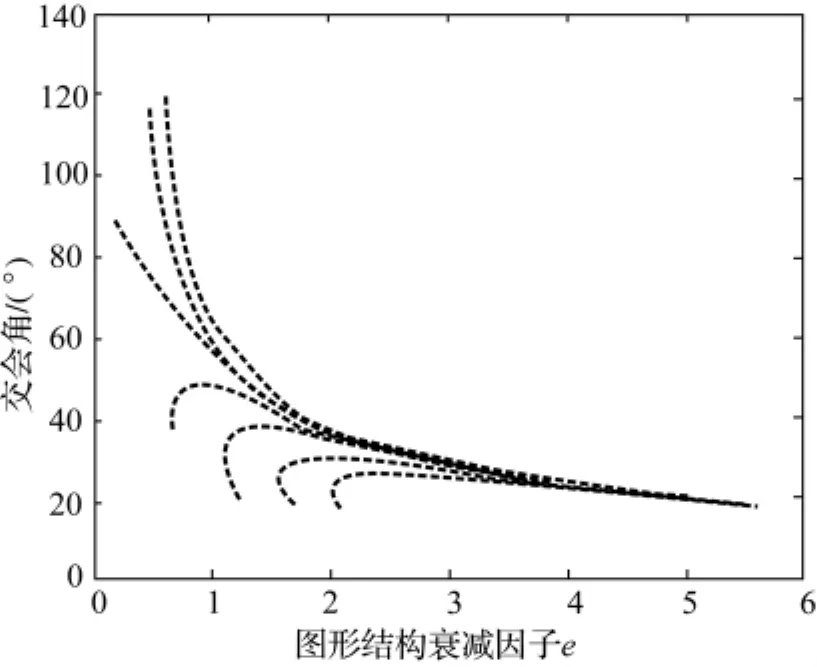
图4 图形结构衰减因子与交会角的关系
图5绘制出了GDOP的空间分布,图中两台经纬仪分别设置在X轴线0 mm及3 000 mm处。从图中看出,距离两经纬仪连线距离相同的点,GDOP两边偏大,中部较小;距离两经纬仪连线越远的点GDOP越大。依据GDOP的空间分布状况,在实际测量中应合理设置两台仪器的位置,使得大部分测点位于两台仪器的中部位置,以提高交会测量精度。

图5 图形结构衰减因子的空间分布
针对两台经纬仪交会测量系统,表1列出了部分典型测点位置的图形结构衰减因子。
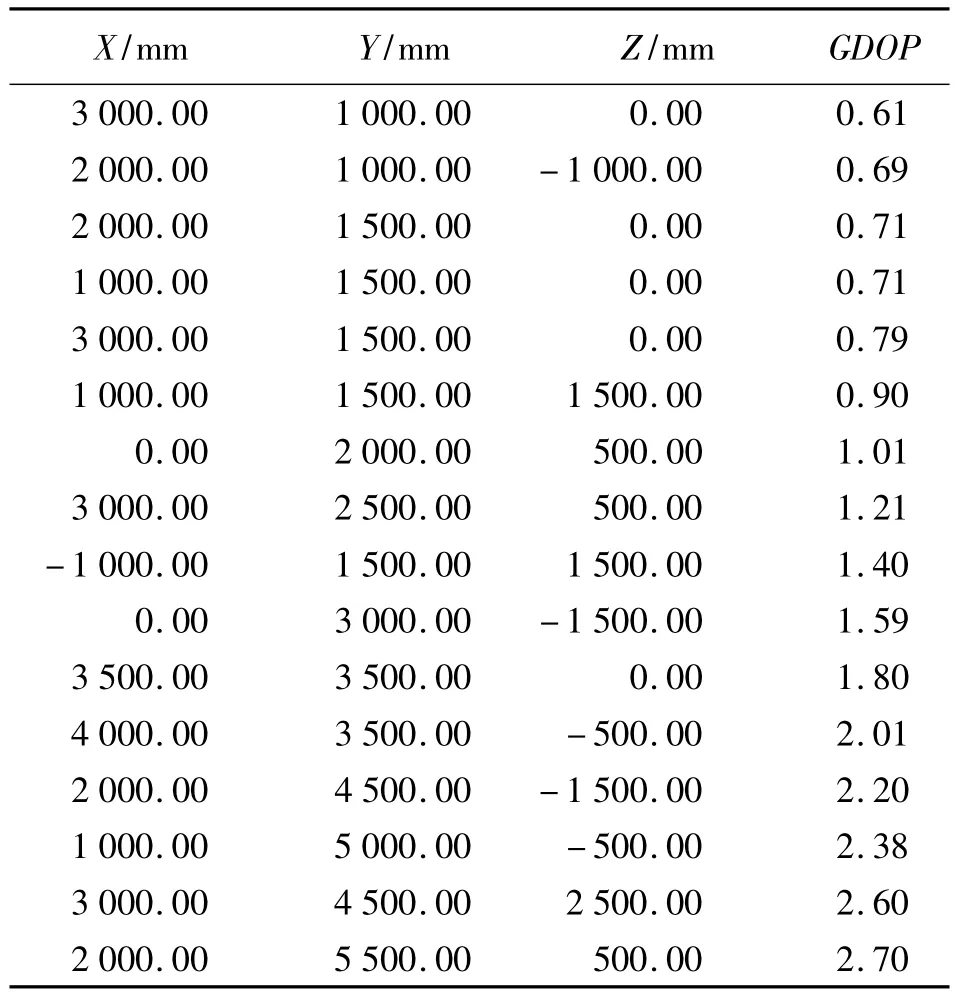
表1 部分典型测点位置的GDOP
三、交会测点误差与GDOP的关系仿真
经纬仪交会测量系统的原始观测值为水平方向值及垂直方向值,其误差源主要为角度观测误差。依据大量的试验表明,采用T3000、TM5100等类型的经纬仪,综合各项因素后的测角误差约为1.5″~2.0″[11,15]。
仿真分析的过程为:①模拟一套测站及交会测点的三维坐标;②依据测站及点的三维坐标反算出观测值,这些观测值为模拟真值,不存在误差;③依据正态分布产生一系列角度误差,将所产生的随机误差加在模拟的观测值真值上,形成一组具有误差的观测值,其误差的大小与实际测量中可能出现的误差大小一致;④依据模拟观测值交会解算点的坐标,与已知的点坐标进行比较求出差值,可认为该差值是由于加入随机误差而产生的交会测点误差,以此作为实际交会测点的误差。仿真中,采用了表1列出的点,并考虑不同测量人员的仪器操作水平,分别取水平角仿真误差的标准差为1.0″、1.5″、2.0″、2.5″、3.0″,对应的垂直角仿真误差的标准差为1.5″、2.0″、2.5″、3.0″、3.5″;将统计出的测点误差与GDOP绘制成如图6所示的关系趋势图。
由图6可以看出,交会测点误差大小与图形结构衰减因子有非常明显的规律趋势,测点误差随GDOP的增加而增大。仿真分析表明,所定义的图形结构衰减因子能较好地反映交会图形结构优劣,是反映交会测点精度的重要指标。
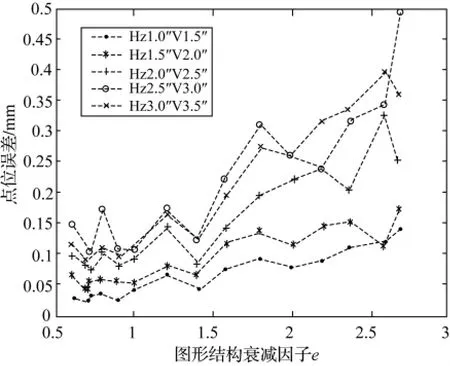
图6 交会测点仿真误差与GDOP的关系
四、实测数据
为进一步验证GDOP与交会测点误差间的规律,笔者在某试验场进行了实测试验。在该试验场中有28个已知三维坐标的点,均匀分别在约11 m× 30 m的范围内,这些点采用激光跟踪仪设置多站进行测量,平均点位误差约为0.05 mm,相对于经纬仪交会测量,这些已知坐标可作为真值。在该试验场内设置两台徕卡TM5100电子经纬仪,构成交会测量系统对这28个点进行交会测量,得出28点的测量坐标。将交会测量坐标与已知坐标比对求出差值,作为交会测点的实际误差,表2列出了这28个点的坐标差值。
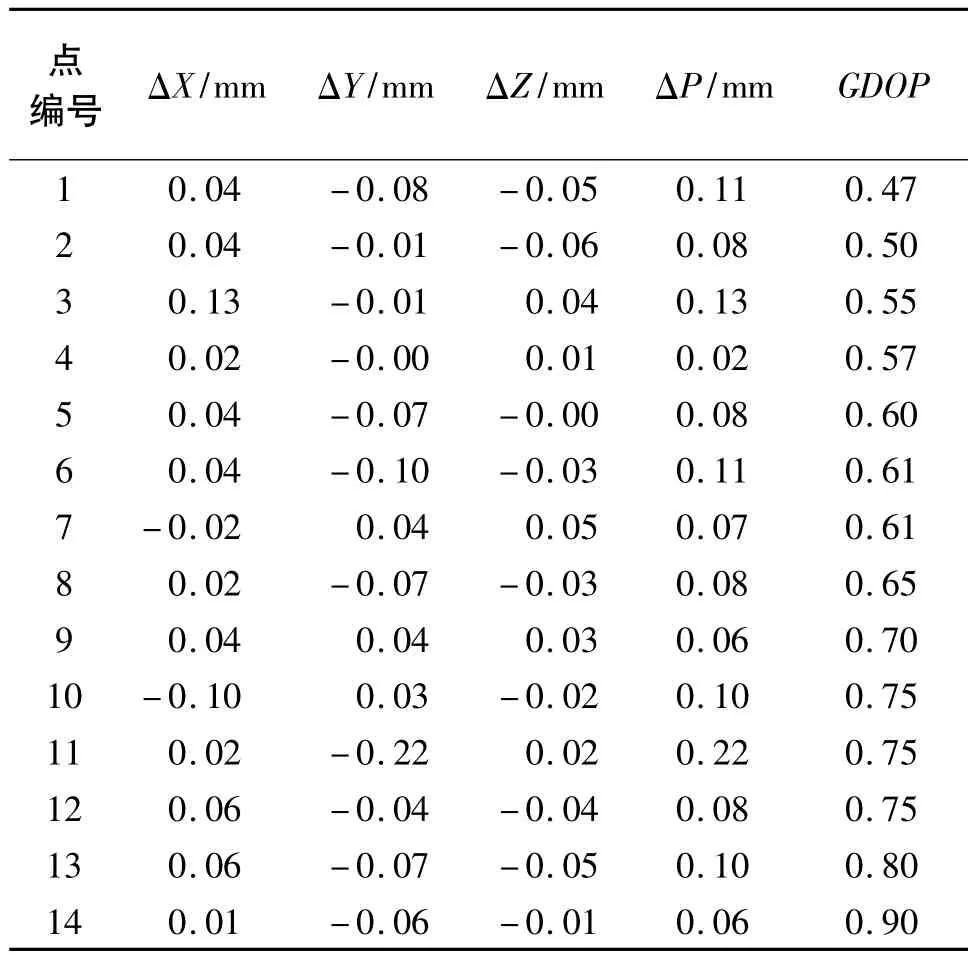
表2 交会测点坐标与已知坐标的差值
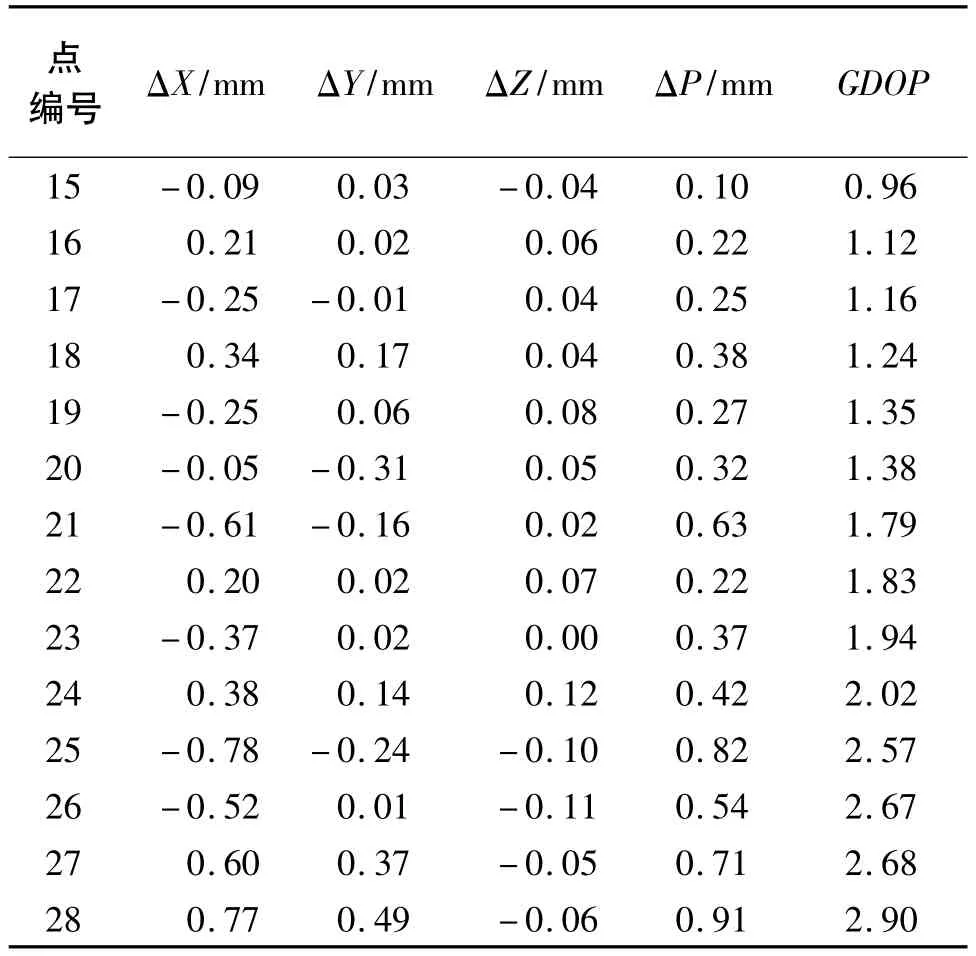
续表2
表2中,ΔX、ΔY、ΔZ分别为三维坐标差值;ΔP为ΔX、ΔY、ΔZ的平方和根。从表2中数据可以看出,当GDOP增加时,实际的交会测点误差随之增加。将GDOP作为横轴,实际交会测点误差为纵轴,绘制出如图7所示的关系趋势图。

图7 实际交会测点误差与衰减因子关系趋势
五、结束语
对于两台经纬仪构成的交会测量系统,其交会测点精度受图形结构优劣影响很大,如何评价图形结构是控制测点误差大小的重要途径。仿真分析及实测数据结果均表明,文中所定义的图形结构衰减因子与交会测点误差间具有显著的规律趋势,是图形结构优劣评价的量化指标。系统操作人员可依据图形结构衰减因子e合理布置测站,并指定相应的限制条件,保证图形结构处于良好的状态,从而达到控制交会测点误差的目的。
[1] 李广云,倪涵,徐忠阳.工业测量系统[M].北京:解放军出版社,1994.43-44.
[2] 陈继华,黄桂平,李广云.一种新的经纬仪/全站仪工业测量系统标定算法[J].测绘通报,2006(8):19-23.
[3] 熊春宝,叶声华.经纬仪工业测量系统的模型研究[J].武汉测绘科技大学学报,1998,23(3):232-237.
[4] 周富强,张广军,江洁,等.现场双经纬仪三维坐标测量系统[J].机械工程学报,2004,40(1):165-169.
[5] 黄桂平.多台电子经纬仪/全站仪构成混合测量系统的研究与开发[D].郑州:信息工程大学,1999:36-41.
[6] 李广云.工业测量系统最新进展及应用[J].测绘工程,2001,10(2):36-40.
[7] 李宗春,李广云,汤廷松,等.电子经纬仪交会测量系统在大型天线精密安装测量中的应用[J].海洋测绘,2005,25(1):26-30.
[8] 王晋疆,金素坤,邸旭,等.经纬仪测量系统在工业测量中的应用[J].光电工程,2003,30(1):53-55.
[9] 潘延玲,常国全.电子经纬仪三坐标精密测量[J].测绘信息与工程,2002,27(4):16-18.
[10] 王晋疆,刘文耀,蔡怀宇,等.电子经纬仪工业测量系统的布设[J].天津大学学报:自然科学与工程技术版,2003,36(6):757-760.
[11] 高宏.非正交系坐标测量系统的原理、检定及应用[D].郑州:信息工程大学,2003:34-36.
[12] 许其凤.GPS卫星导航与精密定位[M].北京:解放军出版社,1994:124-126.
[13] 马岩,谢京稳.改善导航系统GDOP的一种途径[J].装备指挥技术学院学报,2002,13(3):52-54.
[14] 文富忠,孙克宇,徐定杰.基于GDOP的导航定位误差和最优岸台设计算法的研究[J].哈尔滨工程大学学报,2002,23(2):47-50.
[15] KINSTON A A.Electronic Theodolites Distinguishing Features and Sources of Error,and Their Impact on Field Performance and Observational Procedures[D].Toronto:University of Toronto,1991:130-141.
A Measure for Geometrical Figure of Bino-theodolites Based Space Intersection System
WANG Yaohua,CHEN Jihua
0494-0911(2011)06-0011-04
P213
B
2011-04-15
王耀华(1972—),男,甘肃庄浪人,硕士生,工程师,主要研究方向为工程测量与卫星导航定位理论。
