几种常用分布的总体均值方差的经验似然比置信区间估计

崔恩华, 孙 坤

(中国矿业大学 理学院, 江苏 徐州 221116)

几种常用分布的总体均值方差的经验似然比置信区间估计

崔恩华, 孙 坤

(中国矿业大学 理学院, 江苏 徐州 221116)

总体; 均值; 方差; 经验似然

0 引言

经验似然是Owen1988年提出的一种非参数统计推断方法,它与传统的统计方法比较有突出的优点,如用经验似然方法构造的置信区间具有域保持性、变换不变性及置信域的形状由数据自行决定,还有Bartlett纠偏性和无需构造轴统计量等优点.正因为如此,这一方法引起了许多统计学家的兴趣,将这一方法应用到各种领域,得到很大的发展!本文针对几种常见分布的总体,在更一般条件下给出总体均值、方差的经验似然比估计的置信区间.

1 几种常见分布的总体均值方差的经验似然

对几种常见分布的总体我们可以在更一般条件下,得到它们参数的经验似然估计,主要结果如下:

在均值未知的情形下,利用经验似然方法,同时给出总体均值方差的经验似然置信域.

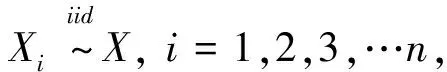
2 主要结果的证明

为了证明定理1、定理2,我们给出下面的引理.

引理1、引理2的证明见文献[3].

下面我们证明定理1,定理2.

证明首先,分四种情况来证明定理1成立.

情况1: 当随机变量X～E(λ)时

情况2: 当随机变量X～P(λ)时

类似于求解A2,A3,A4的方法易知

A1=λ4+3λ3+λ2.

故E(X4)=λ4+6λ3+7λ2+λ

情况3: 当随机变量X～B(n,p)时

J1+J2+J3+J4.

3n(n-1)p2,

类似于求J4,J3的方法易知

J2=3n(n-1)(n-2)p3+3n(n-1)p2，

类似于求J4,J3,J2的方法易知

J1=n(n-1)(n-2)(n-3)p4+3n(n-1)(n-2)p3+n(n-1)p2.

E(X4)=n(n-1)(n-2)(n-3)p4+6n(n-1)(n-2)p3+7n(n-1)p2+np.

情况4: 当随机变量X～Γ(α,β)时

[1] 段智力, 倪志坤. 正态总体均值方差的经验似然比置信区间估计?[J].白城师范学院学报, 2009(12):7-8.

[2] Owen A. B Empirical likelihood?[M].Chapman amp; Hall, New York, 2001.

[3] 王启华. 经验似然统计推断方法发展综述?[J].数学进展, 2004 (2): 141-151.

[4] 李朝阳，王伯成. 方差的经验似然比置信区间估计?[J].工科数学, 1996 (1): 48-56.

[责任编辑：李春红]

EmpiricalLikelihoodRatioConfidenceIntervalEstimationforsomePopulationParameters

CUI En-hua, SUN-Kun

(College of Science China University of Mining And Technology, Xuzhou Jiangsu 221116, China)

This paper discusses the joint maximum likelihood estimation of general mean-variance according to the unknowing of some population mean, as well as give the confidence interval of empirical likelihood about variance in the situation of unbiased estimators instead of mean.

population; mean; variance; empirical likelihood

O212.7

A

1671-6876(2011)02-0106-04

2011-01-16

崔恩华(1984-), 男, 江苏连云港人, 硕士研究生, 研究方向为数理统计.