量子力学双语教学实践

凌东波 明 燚

（安徽大学物理与材料科学学院，安徽 合肥 230039）

量子力学双语教学实践

凌东波 明 燚

（安徽大学物理与材料科学学院，安徽 合肥 230039）

量子力学是物理专业本科阶段重要的课程之一。双语讲授量子力学在安徽大学是一次有益的尝试，在这一教学过程中，有相当多的实践经验值得总结。

束缚态；经典类比；狄拉克符号

1 采用的教材

我们采用 Griffiths的著作 “Introduction to Quantum Mechanics”[1]。这一著作写法上适合初学者，是很有特色的一本教材。兼顾了详细的计算和清晰的物理概念，注重阐述物理理论产生的背景和动机。具体体现在以下方面

1.1 直接引入薛定谔方程。这种讲法很直接，相比较流形的国内教科书的引进方式[2]，这是容易讲授的方式。我们知道薛定谔方程的获得是通过和经典力学的类比猜得的，所有的推导都是辅助性的，而不是真正的。从这个意义上讲，直接的引入该方程可以减少很多概念上的困惑。另外，这也是实验要求的。关于线性叠加，去年有一个实验方面的工作[5]。

这本教科书里引入动量算符的方式是通过位置平均值对时间的求导的方法，这种方式或许可以改成直接的定义动量算符更加合适。因为动量算符的是从经典力学中的Poisson括号类比获得的，这可以参考狄拉克的著作[4]。

1.2 对束缚态有很直观而准确的定义。经典力学中的粒子具有的动能如果低于两侧势垒的高度，那么该粒子处于束缚态。束缚态的本意在于该粒子所处位置是局域的，也就是在无穷远处不会出现该粒子。在量子力学中，则需要对应于波函数在无限远处为0。考虑到量子力学中波动性，经典禁区依然有可能出现粒子，所以束缚态的定义为，粒子具有的能量低于无限远处的势能。这一关于束缚态的准确定义非常直观，而且体现了量子力学和经典力学的对比。

1.3 对现代的热点问题有追踪。比如几何相位问题。这里采用了Berry的原始文献中的方式解释AB效应。Berry相位和AB效应背后都隐藏了深刻的物理内容，和参数空间的拓扑性质有关，同时也显示，经典力学中完全不可观测的规范，在量子力学中是可以间接的观测。 这里采用了直观的方式，通过与经典力学中傅科摆问题的比较，引入量子力学中的不可积相位。一个本科生完全可以重复这些计算。

1.4 氢原子模型中的计算采用渐近分析的方法，避免了合流超几何方程的直接求解。这一方法借鉴于狄拉克的教材[4]。采用渐近分析，可以把原来有正则奇点的微分方程变形为没。

1.5 在散射的波恩近似中，关于传播子的计算方法，有一点疏忽。本书的计算没有考虑到边界条件，认为绕过pole的方法是确定的。但是事实上，绕过pole的方式由边界条件决定的。教科书忽略了边界条件的作用，而这一影响是至关重要的。

1.6 在处理不确定度关系中，采用了严格的方法。不确定度关系（旧称测不准原理）中，关于时间和能量的不确定关系

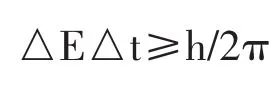
这一表达式有一个问题，时间并不是力学量，如何定义其不确定度？我们通常的解释是，时间的不确定度是状态的寿命。但是在单粒子量子力学中，寿命没有良好定义。严格的方式是定义

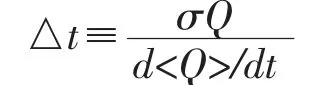
这里的σQ是某一力学量Q的不确定度。根据这个定义，我们发现时间的不确定度并不唯一，随我们选取的力学量的不同而不同。这样就解决了前面的矛盾。

1.7 本书对谐振子和角动量的处理都是以代数方法为主，微分方程的方法作为辅助。代数方法处理角动量问题才能计算CG系数。虽然CG系数的计算不属于本科生必须掌握的内容，但是这种代数方法往往反映更深刻的物理含义，实际上这和SU（2）代数直接相关，为将来深入的学习角动量理论准备了基础。

值得注意的是，电磁场中的带电粒子的运动方程没有详细的讨论，这个和国内教学大纲上有差异，如果讲授这一内容需要讲授者自己增加。

2 教学的特色

2.1 强调经典和量子的对比

强调量子和经典的对比。量子力学中采用波函数描述粒子的运动状态，这一方式和经典力学中采用质点完全不同。质点的概念符合人类的直观，而波函数是反直觉的。

尽管如此，量子力学中又有很多概念和经典力学是不可分割的。比如束缚态的定义，力学量算符的写法，力学量的对易关系和经典力学中的泊松括号。

我们初学者往往关心一些非常根本的问题，比如“为什么用波函数表示状态？”我们对波函数的出现非常的不适应。这里我有一个比较哲学化的观点，如果我们问问自己，为什么经典力学中的运动的物体可以抽象成一个点？为什么刚体可以看作是连续的质量分布？如果我们追问这样的为什么，我们发现，我们自己也无法回答这样的问题。经典力学中关于质点的假定更加直观，所以容易被我们“接受”，注意是“接受”。当我们学习量子力学的时候，我们的问题是试图去“理解”波函数。如果我们用同样的态度对待波函数，我们应该是接受波函数而已。虽然波函数是违背直观的概念，但是物理学不断发展的过程实际上就是不断违背直观的过程。

2.2 注重数学推导

量子力学中采用的数学技巧主要是线性代数，用狄拉克的话说，量子力学和相对论都是变换的理论。所以熟练的掌握线性变换以及变换所具有的直观的物理和几何含义/是非常有必要的。比如在角动量理论的部分，讲述CG系数是比较艰难的。其困难来源于学生对线性代数的理解不够深刻，所以要强调不变子空间和简并的关系。而不变子空间的概念在简并微扰论当中起了重要的作用。从这一例子可以看出，只有不回避复杂的数学推导和提升数学概念，才能进一步深入的理解物理概念。

2.3 强调微扰论的价值

量子力学中的微扰论对应的可观测的效应。如果没有微扰论，我们就无法检验量子力学的正确。比如光谱学实验得到的氢原子能谱，这个过程本身就是微扰的结果，因为物理学中的观测总是和微扰相对应的。

同时，本科阶段学习的固体物理学中，弱周期的势能可以导致能谱中的禁带这一结果，恰恰是简并微扰论的结果。所以克服微扰论的计算的复杂，抽取其中物理的思想和实用价值是非常必要的。

2.4 强调狄拉克符号的使用

狄拉克符号在计算上可以简化运算。尤其在代数解法当中，我们并不需要明确的表象，此时狄拉克符号的使用几乎是不可避免的。

另外狄拉克符号有助于澄清理解波函数。事实上量子态不仅仅是不可观测的，而且本身是需要表示的。只有清楚的理解了狄拉克符号，我们才能更好的理解位置表象中的波函数是量子态的表示，也更好的理解位置表象中的动量算符的形式。狄拉克符号的讲授我们借鉴了Sakurai的著作[3]。

2.5 教学效果

我们经常的和学生讨论他们遇到的困难，了解他们对课程的掌握情况。

从效果上看，选修该课程的同学几乎都能跟上进度，有部分学生对量子力学有比较学生经过认真的计算，发现了教科书上的一些问题，比如前面所提到的波恩近似中的传播子的计算问题。从他们后来参加研究生入学考试成绩来看，他们对该课程的掌握是相当好的。

3 致谢

感谢安徽大学物理与材料科学学院李刚老师的有益讨论。师的有益讨论。

[1]David J.Griffiths,Introductiont to Quantum Mechanics[M].机械工业出版社,2007.

[2]曾谨言著,量子力学教程[M].第二版,科学出版社,2008.

[3]J.J.Sakurai,Modern Quantum Mechanics[M].Addison-Wesley Publishing Company,1994.世界图书出版公司影印

[4]P.A.M.Dirac,the Principles of Quantum Mechanics[M].Oxford University Press,1958.科学出版社2008年影印

[5]Urbasi Sinha,Ruling out Multi-Order Interference in Quantum Mechanics[J].Science 2010，329：418

BILINGUAL TEACHING PRACTICE OF QUANTUM MECHANICS

LING Dong-bo MING Yi
（School of physics and material science,Anhui University,Hefei Anhui 230039）

Quantum mechanics is one of the kernel courses for undergraduate students majoring in physics. The bilingual teaching of this course in Anhui University was a useful attempt.Consequently there are many practical experiences worthy of summarizing in the teaching process.

bound states;classical analogy;Dirac notation

A

1672－2868（2011）03－0132－03

2011-2-28

安徽大学质量工程项目（项目编号：2304005）

凌东波（1978-），男，安徽巢湖人。安徽大学物理与材料科学学院讲师，研究方向：凝聚态理论

责任编辑：陈 凤