一种过程支持向量机模型及其若干理论性质

许少华， 庞跃武， 王 兵

( 东北石油大学 计算机与信息技术学院，黑龙江 大庆 163318 )

0 引言

支持向量机(Support Vector Machines，简称SVM)是一种建立在统计学习理论结构风险最小化原则上的模式分类方法[1-2]，具有数学理论完备、算法复杂度与特征空间维数无关、易于实际应用等优点，在很多领域获得成功应用[3-7].在科学研究和工程领域中，存在大量时变信号的模式分类与识别问题，如抽油机井动态平衡状况诊断[8]、地震信号实时监测与辨识[9]、运动图像特征分析[10]等.在SVM模型中，系统的输入一般为与时间无关的常量，即输入/输出之间是几何点式的对应关系，从信息处理机制上无法反映时变输入信号的过程特征和输入过程中的累积效应[11-12]，难以直接分类判别时变信号.

笔者将SVM的分类机制扩展至时域空间，提出一种过程支持向量机(Process Support Vector Machines，简称PSVM)模型.PSVM的输入为时变过程信号，通过核函数变换将动态模式映射到高维特征空间，经过学习训练集中函数样本的类别特性，自适应提取动态模式的过程特征，实现对动态模式的判别；给出PSVM的一般模型，证明PSVM与单隐层前馈过程神经元网络[13]的二分类能力等价；将复杂的动态模式集合非线性地映射到高维特征空间，提高动态模式的可分性；非时变SVM是PSVM的一种特例等理论问题.PSVM放宽传统SVM模型对输入的同步瞬时限制，拓宽支持向量机的应用领域.

图1 PSVM模型

1 PSVM模型

PSVM的输入为时变过程信号，输出为模式类别，其结构由时变信号输入层、核函数变换层和输出层组成(见图1).其中：xi(t)为时变输入信号，x(t)=(x1(t),x2(t),…,xn(t))∈(C[0,T])n,[0,T]为信号输入过程区间；Xj(t)为过程支持向量，Xj(t)∈(C[0,T])n(j=1,2,…,m)；K(·,·)为PSVM的核函数；αj(j=1,2,…,m)为隐层节点到输出节点的连接权；d(X(t))为PSVM的输出.

PSVM模型的动态模式分类规则为

(1)

由图1中PSVM的输入、输出之间的动态信号变换关系，构建3种过程核函数.

(1)多项式核函数：

(2)

式中：(Y(t))T为函数向量Y(t)的转置，Y(t)∈(C[0,T])n.

(2)径向基核函数：

(3)

式中：‖·‖为函数空间(C[0,T])n中的范数；σ为均方差参数.

(3)两层过程感知机核函数：

(4)

式中：βj为性质参数.

2 PSVM性质

PSVM的性质是其对动态模式分类问题应用有效性的基础.

定理1PSVM与单隐层前馈过程神经元网络的二分类能力等价.

证明由PSVM构建1个单隐层前馈过程神经元网络(Process Neural Network，简称PNN)，该PNN可与PSVM实现相同的动态模式二分类.

(1)定义1个结构为n-m-1的PNN.设该PNN的输入层有n个时变函数输入节点，隐层有m个过程神经元节点，其激励函数为PSVM的核函数Kj，时空聚合运算[1,14]由过程支持向量机的核函数变换确定；输出层为1个非时变神经元，该神经元与PSVM输出节点的信息变换机制相同.输入层节点到隐层各节点的连接权设为1，隐层各节点到输出节点的连接权为αj(j=1,2,…,m).显然，所构建的PNN与PSVM具有相同的信息处理机制，可实现对时变函数样本集S相同的二分类.

(2)设PNN为由n个输入节点、m个过程神经元隐层节点和1个非时变神经元输出节点组成的多输入单输出系统，二分类训练样本集为S.PNN隐层m个过程神经元节点对应的激励函数为Kj(j=1,2,…,m).当m>n时，K=(K1,K2,…,Km)将S中的样本映射到高维特征空间.设PNN输入层节点与过程神经元隐层节点的连接权为wij(t)(i=1,2,…,n;j=1,2,…,m)，隐层各节点到输出节点的连接权为αj(j=1,2,…,m).定义PSVM的核函数变换为过程神经元在过程区间[0,T]上的时空加权聚合运算的激励输出，过程支持向量取为Wj(t)=(w1j(t),w2j(t),…,wnj(t))(j=1,2,…,m)，输出单元为PNN的输出神经元，输入层节点到核函数变换层各节点的连接权为1，核函数变换层各节点到输出层节点的连接权为αj(j=1,2,…,m)，则定义一个结构为n-m-1的PSVM(见图1)，且该PSVM与PNN关于训练样本集S具有相同的二分性.

单隐层前馈过程神经元网络具有连续性，以及对满足Lipschitz条件泛函和连续泛函的可逼近能力[14-15]，因此PSVM对复杂动态模式具有很强的分类能力.

定理2传统支持向量机是过程支持向量机的一种特例.

证明在过程支持向量机模型中(见图1)，令系统输入为与时间无关的常量，即X(t)=(x1,x2,…,xn)∈Rn.此时系统输入由时变函数变为非时变数值(或数值向量).将过程核函数替换为非时变核函数，即取核函数K(X(t),Xj(t))=K(X,Xj)，则PSVM模型简化为一般SVM模型.

定理3将复杂的动态模式集合非线性地映射到高维特征空间，提高动态模式的可分性.

证明设S为包含N个时变模式向量Xi(t)(i=1,2,…,N)的集合，其中Xi(t)∈(C[0,T])n，且Xi(t)属于2个模式类χ1和χ2之一.若存在非线性函数K(X(t))=(K1(X(t)),K2(X(t)),…,Km(X(t)))，可将S中的点一一映射到1个新的m维特征空间(m>n)，记映射点的全体为H(H为由泛函K生成的集合S的特征空间).H中的点表示为

K(Xi(t))={K1(Xi(t)),K2(Xi(t)),…,Km(Xi(t))},Xi(t)∈S,i=1,2,…,N.

(5)

如果存在一个m维向量ω，使得

(6)

则称1个关于S的二分{χ1,χ2}是φ可分的.其中，由方程K(X(t))·ω=0定义的超平面描述特征空间H中2类样本的分离曲面.

从概率角度分析，1个动态模式集合的二分问题可被看作是1个依赖于所选择的分类原则，以及样本函数空间中动态模式分布的随机事件.假设动态模式向量X(t)=(X1(t),X2(t),…,XN(t))，根据动态系统的概率特性独立选取，同时所有关于S的二分为等可能.令P(N,m)表示某一随机选取的二分是K可分的概率，则根据Cover定理[16]，P(N,m)表示为

(7)

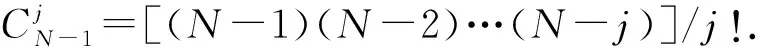
式(7)表明特征空间H的维数m越高，则概率P(N,m)越趋向于1.这证明,通过将复杂的动态模式分类问题非线性地映射到高维数特征空间，比在低维数特征空间中更可能使模式可分.

3 结束语

针对时变信号的分类问题，建立一种过程支持向量机PSVM模型，对其分类能力、模式可分性、传统SVM是PSVM的一种特例等性质进行证明.PSVM将传统SVM的信息处理域扩展为时变空间，可直接将时变过程信号作为SVM模型的输入，简化传统动态分类方法需要预先提取时变信号形态特征的过程，扩大SVM的应用领域，对于时变对象的模式分类等问题的解决具有重要意义.