风力机远尾流的计算研究

田琳琳，赵 宁，钟 伟，胡 偶

(南京航空航天大学航空宇航学院，江苏南京 210016)

0 引言

风力机是将自然界的风能转化为机械能并获得电能的装置。由于能量的转移，风经过旋转的风力机之后，流动情况发生了很大的变化:风速减小、湍流强度增加、出现了明显的风剪切层。风速减小会使下游风力机的输出功率降低，尾迹附加的风剪切和强湍流会影响下游风力机的疲劳载荷、使用寿命和结构性能。经过一段距离之后，在周围气流的作用下，风速逐渐得到恢复。这就是风力机的尾流效应［1］。为了使有限面积的风场产生最大的经济效益，风电场开发商尽可能多在风场内布置风力机，这样上游机组会对下游机组产生较大的尾流效应，导致下游机组发电量减少，进而降低整个风场的总输出功率。因此，开展尾流效应对风力机性能影响的研究对合理布置风力机，减小尾流对下游的影响，提高风能资源的利用效率，减小风电场的占地面积，最终使风电场的经济性达到最佳起着重要的作用。

风力机的尾流区分为近尾流区和远尾流区。近尾流区的研究着眼于功率提取的物理过程和风机性能，而远尾流区的研究重点是尾流模型、地形影响、湍流模型的恰当选取，更着重于研究风电场机组间的相互干扰［1］。

许多专家学者对风力机的尾流效应开展了广泛的计算研究。可以将这些研究大致分为两类:一类是尾流模型研究，这些模型是由学者提出的简化的尾流模型，然后利用实验数据检验模型并进行修正，主要用来解决工程问题。如风资源分析软件WAsP采用的Park模型［2］以及Ainslie提出的涡粘性尾流模型［3］等等。另一类是流动机理研究，该部分主要是回归基础研究，旨在揭示流动的内在规律和本质。如早期的动量－叶素理论［4］和涡尾迹方法［5］。之后随着计算机的发展，又出现了很多基于CFD的方法，例如Ivanell等学者［6］使用了制动线(ACL)方法研究了单个风力机的近尾迹区的流动状况，Sankar等学者构造了N－S方程、全势能方程与自由涡尾迹相混合的方法用于求解水平轴风力机周围的非定常粘性流场［7］。Sørense［8］等使用 RANS 方程进行流场的全三维数值模拟。

本文提出了两种方法用来研究单个风力机的远尾迹特征。第一种方法为修正的Park模型，由初始的一维Park模型进行三角函数修正得到。Park模型由于计算量小且相对准确［9］，在工程上得到了广泛的应用，经过修正的Park模型计算量也很小，且在径向方向的速度型更接近于真实的流场分布情况。第二种方法是结合制动盘理论和CFD［10］，将风力机简化成为一个无限薄的产生压力跃升的制动盘，采用FLUENT商用软件提供的Fan边界对流场进行数值模拟。该方法较之建立真实的风力机模型并进行模拟来说，降低了计算量和计算复杂度，为风力机的微观选址提供很好的理论支持。最后将本文的两种数值方法的结果与风洞实验结果以及Park模型的预估结果进行对比分析，发现这两种方法都能够很好地预测风力机的尾流流场。

1 研究模型

1989年 Garrad Hassan在 Marchwood工程实验室(MEL)开展了一系列的风力机尾流的实验研究［11］，所选用的实验对象为模型缩比尺度为1/160的水平轴风力机。对于真实尺度的风力机来说，能反映其性能的重要的参数就是推力系数，所以在风洞试验中，观察了风力机在三个不同尖速比下的气动性能。三个不同尖速比 λ =2.9，λ =4.0 ，λ =5.1 对应的轴向推力系数分别为 CT=0.62，CT=0.79 ，CT=0.85 。

本文选用的计算模型为Hassan实验的缩比模型所对应的真实模型，即风轮直径为43.2m，轮毂高度为50m，地表粗糙度为0.075m，相当于风力机树立于短的农作物覆盖的真实地形之上。

2 计算方法

2.1 Park模型的修正

Park模型是由学者Jensen于1986年提出的一维尾流模型［2］，该模型假设在风力机下游，尾流是线性膨胀的，Park模型的原理图如图1所示。根据质量守恒定理推导出在风力机下游x位置处速度为:

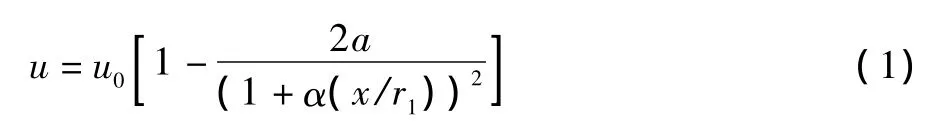
其中u0为来流风速，a为轴流诱导因子，与推力系数CT有关，r1为下游x位置处尾流区域的半径，α为尾流扩散系数，表示尾流的膨胀速率。a、r1和α的公式如下:

其中，rr为风轮半径，z为风力机轮毂高度，z0为地表粗糙度。

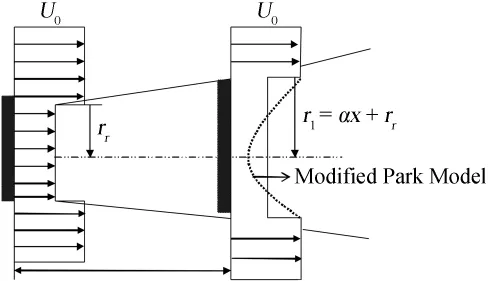
图1 尾流模型原理图Fig.1 Schematic of wake model

大量的实验结果以及数值模拟表明，在真实的尾流流场中，沿风力机径向的速度分布应该为抛物型的［12］，这与三角函数的图形有着很大的相似性，故在此使用三角函数对一维的Park模型进行修正，使其为二维模型，保证修正后的径向速度型为抛物型。修正后的Park模型示意图如图1所示。

令y方向为径向方向，假设修正后的速度分布符合标准的三角函数关系式:

下面将分别求解A，k以及b。根据余弦函数周期的定义可得:

假设余弦函数取最大值时所对应的径向位置为r1即膨胀尾流的半径，则有:

基于修正前后动量守恒的原则，也就是说修正后的总动量与Park模型推导出的总动量相等，即速度型下所包含的面积相等，有:

联立(6)～(8)式分别得到:

可得u*的表达式为:

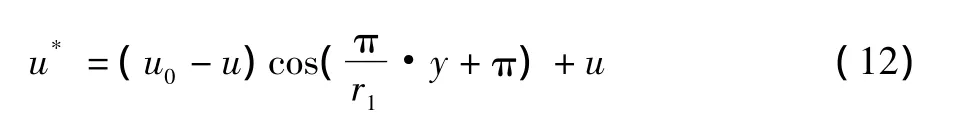
所以经过修正的Park模型分为两步:

2.2 制动盘理论结合CFD方法

当空气经过风轮盘时，由于风力机的阻塞作用，使得流管内的风速降低，根据质量守恒原理，流管的横截面积就会膨胀以适应减速的空气，我们将风轮所在平面称为制动盘［12］。

由经典的Rankine－Froude原理可知，风经过制动盘时，会在制动盘前后产生压差，压差的表达式如下:

其中为△P空气经过制动盘时产生的压力降，ρ为空气密度，U0为来流速度5.3m/s，a为轴流诱导因子，见式(2)。

把风力机简化为产生压力降的制动盘，这与商用软件FLUENT提供的Fan的物理模型具有相似性，所以可借助Fan边界来模拟风轮，计算Fan对整个流场的影响。在FLUNT中，把Fan假设为一个无限薄的面，流体经过这个面时出现压力跃降，而跃降的大小是速度的多项式函数，压强跃降函数的表达式为:

在式(13)中△P为压强跃降量，fn为多项式系数，v为速度。这样做的目的是把Fan前后的速度变化转化成压差项反映到流动方程中。

在本文的计算中，将风力机简称为一个无限薄的制动盘，并根据风力机的推力系数与风速关系的特征曲线设定制动盘前后的压差。然后在全流场内求解带湍流模型的N－S方程。

3 计算结果与分析

3.1 风轮中心轴向速度分布

能否准确地计算尾流轴向动量亏损是判断一个模型是否能够很好地预测尾流发展情况的一个重要指标。图2给出了在三个不同尖速比下，制动盘结合CFD方法、Park模型以及风洞实验这三种方法分别得到的沿风轮中心的速度轮廓图。在图中，x方向是来流速度方向，D为风轮直径，U是尾流的当地速度，U0是无穷远处的来流速度。由于Park模型在风轮下游的两倍风轮直径之后才有效，所以本文选择从风力机下游的2D距离之后对三种方法进行分析比较。图中很明显地反映了风力机的下游速度会下降，经过一段距离之后，逐步恢复到来流速度。且随着尖速比的增加，推力系数就会增加，尾流效应就越明显。在下游6D之前，Park模型和本文的制动盘结合CFD方法都偏大很多，是因为这两种方法都没有考虑到风力机的旋转效应，而真实的风洞试验中，风力机是旋转的，旋转会引起风力机的下游产生很强的湍流以及尾涡，尾涡通过发展、破碎等过程会耗散掉空气中很多的能量，导致下游的速度进一步降低。Helmis等学者［13］指出风洞实验过高预估了近尾迹区的尾流效应，使分析得出的风轮中心的速度亏损较大。这也是本文方法的结果与风洞试验结果在近尾流区相差较大的原因之一。

开展尾流效应研究的目的是在风电场内合理布置风力机，风力机的安装间距要满足风场总体效益最大化的目标。通过对国内外风场多年的建设经验分析，风力发电机组安装间距在盛行风向上选择为6～10倍风轮直径，在垂直盛行风向上选择为3～5倍的风轮直径较为合适。在下游距离为6～15倍风轮直径之间，本文的制动盘结合CFD方法的计算结果与实验值吻合的很好，而Park模型的计算结果偏高。这说明本文的计算方法可以为风电场的微观选址提供很好的理论依据。

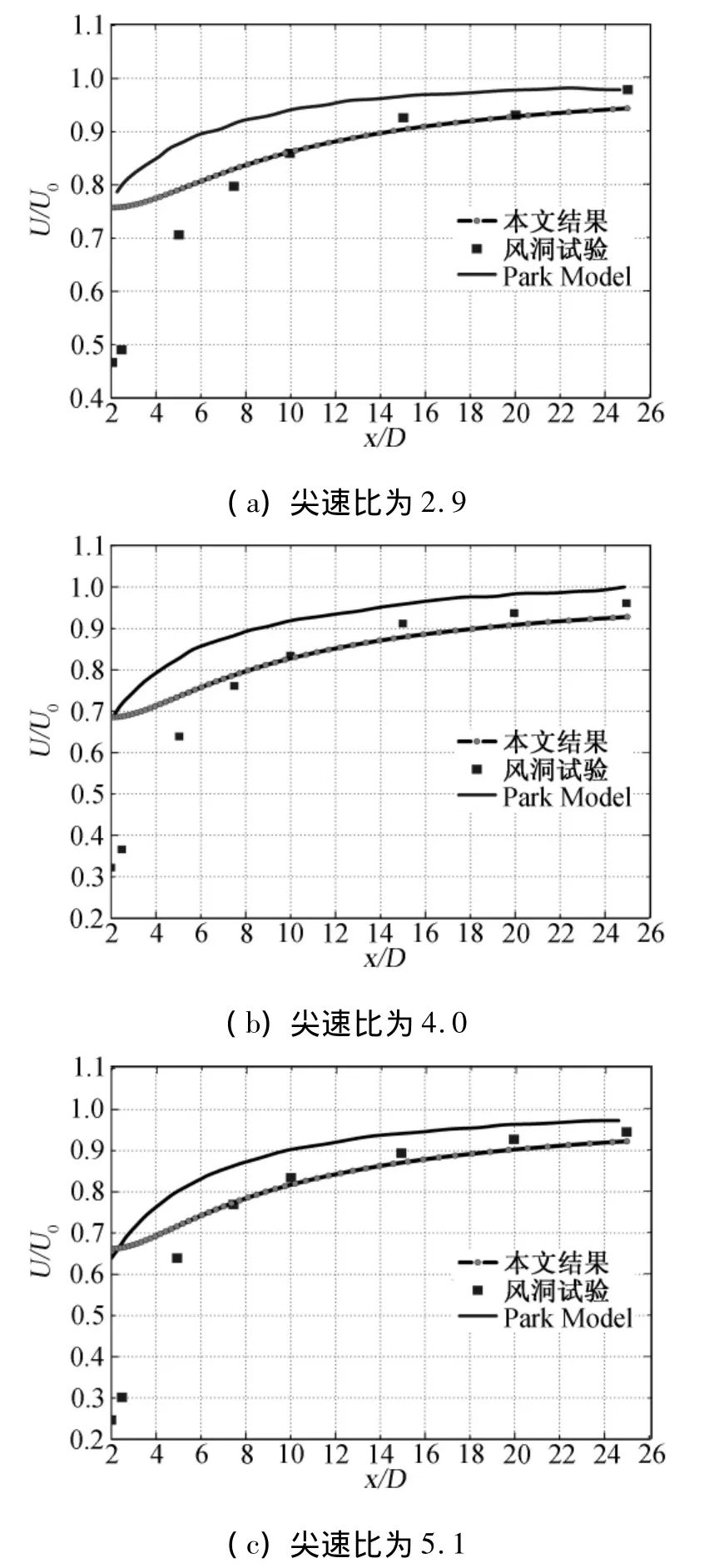
图2 风轮中心轴向速度分布Fig.2 Velocity deficit on the wake centerline

在风力机下游15倍风轮直径之后，Park模型的计算值比实验值偏大，本文的计算结果偏小，说明尾流还没有来得及完全恢复。

3.2 下游位置的径向速度分布

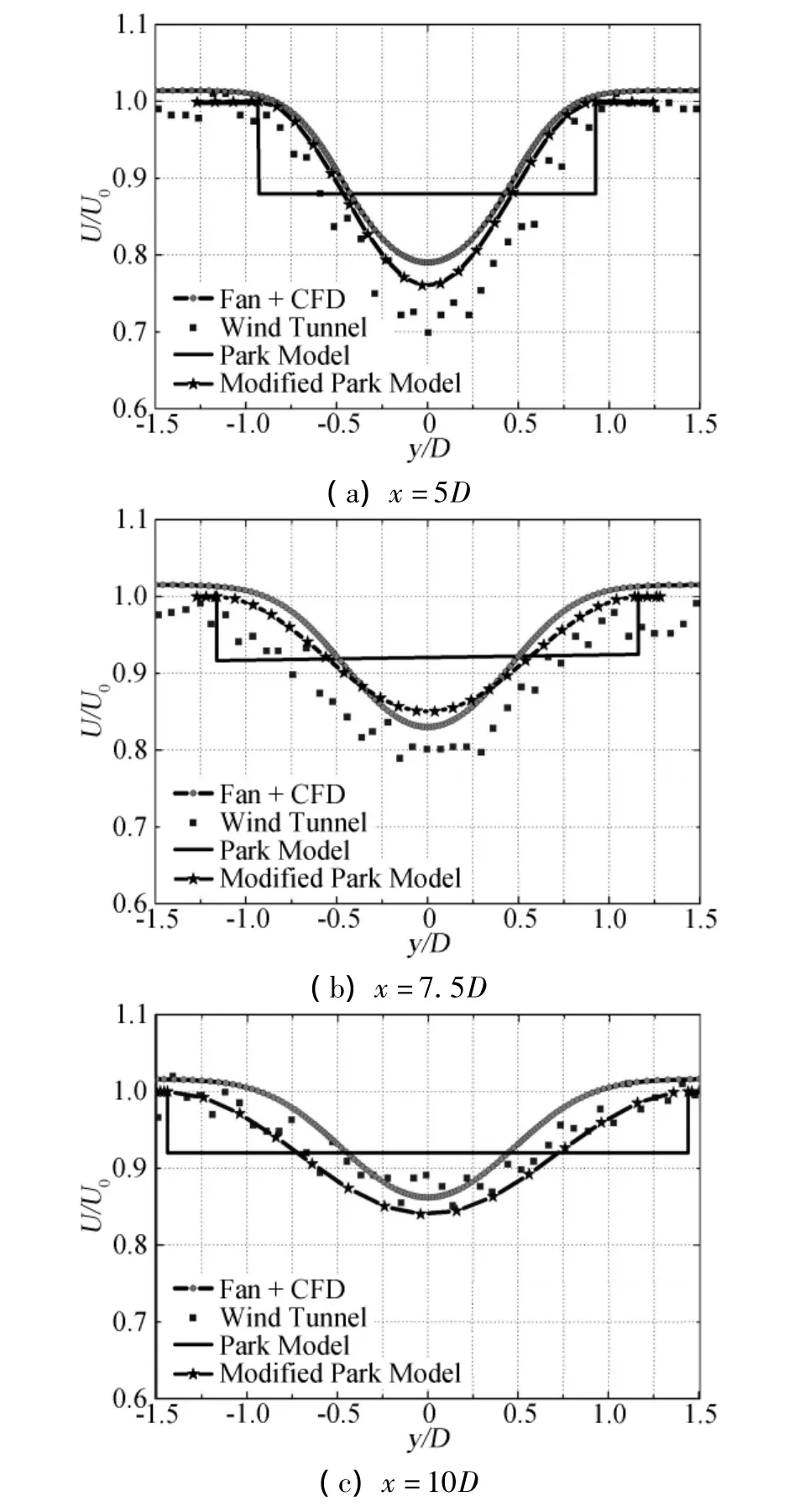
图3 尖速比2.9时，风力机下游的不同位置处的径向速度分布Fig.3 The crosswind profiles of mean velocity at hub height for the tip speed ratio of 2.9

图3和图4分别给出了不同尖速比下风力机下游的不同横截面在风轮高度处的径向速度分布。该图明显的显示了尾流效应，且尖速比越大，尾流效应越明显。从整体来看，Park模型以及本文的制动盘结合CFD方法的计算结果都大于实验结果，这是因为在风力机下游的一段距离之后，压差不再在整个流动中起主导作用，而是湍流强度以及尾涡的变化主导着整个流场的能量变化，在真实情况中，风力机下游的尾涡会逐渐耗散掉，导致能量的降低，进而速度会降低。在越靠近下游的地方，制动盘结合CFD方法以及Park模型结果会更接近风洞试验值，尤其是在尖速比为2.9时，风力机下游10倍风轮直径的地方，本文结果与风洞试验值几乎吻合。从图中还可以看出经过修正的Park模型与风洞试验结果和制动盘理论结合CDF方法计算结果吻合的较好，尤其是在风轮中心两侧，与实验值更加接近。由于其计算量小，计算复杂度低，因此在今后可作为一项计算工具应用于工程实际。图3和图4还反映了制动盘结合CFD方法计算处的尾流宽度略大于Park模型的尾流宽度，更接近于实验值。一个比较有趣的现象是在流管边缘的地方，制动盘结合CFD方法计算的结果比实验值和Park模型的值偏大2%，风出现了稍微的加速现象，这是因为在制动盘的周围拖出来的尾涡从周围流体中吸收了能量，导致速度的稍微上升。

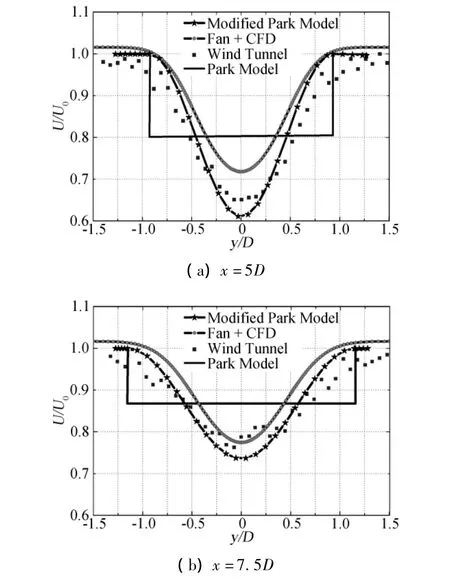
图4 尖速比5.1时，风力机下游的不同位置处的径向速度分布Fig 4 The crosswind profiles of mean velocity at hub height for the tip speed ratio of 5.1

4 总结

本文根据GH公司提供的风力机数据，通过两种方法对单个风力机的尾流进行了计算模拟。一种方法是构造新的尾流模型计算流场速度分布，另一种方法是结合制动盘理论和CFD，在全流场进行数值模拟。当风吹过风力机时，风速会下降，经过下游一段距离慢慢恢复到来流速度，且尖速比越大，尾流效应越明显。从风轮中心轴向速度分布图来看，在下游6倍风轮直径之后，本文结果与风洞试验值的最大误差约为4%。径向速度分布显示了尾流的膨胀系数大概为0.08，越靠近下游，本文计算方法的精度就越高。虽然Park模型没有精确预测尾涡的形状，但是它近似给出了尾涡的发展过程，而本文构造的新尾流计算模型与风洞实验值吻合较好。

将本文两种计算方法的结果与风洞实验以及Park尾流模型进行分析比较，显示了本文能够定性反映风力机周围的物理流动现象。以上结果表明，本文的两种计算方法适用于风力机的流场模拟，可作为工程应用的工具，用于风电场的流场模拟，为风力机的微观选址提供一定的参考依据。

［1］VERMEER L J，SØRENSEN J N，CRESPO A.Wind turbine wake aerodynamics［J］.Progress in Aerospace(Sciences)，2003，39(6 －7):467 －510.

［2］JENSEN N O.A note on wind generator interaction［R］//RisØNational Laboratory，1983.

［3］AINSLIE J F.Development of an eddy viscosity model for wind turbine wakes［A］.Proceeding of 7 th BWEA Wind Energy Conference［C］，Oxford，1985.

［4］GLAUERT H.Airplane propellers［A］.In Aerodynamics theory.Dover Publication Inc:New York［M］，1963，4(Division L):169－360.

［5］BAREISS R，GUIDATI G，WAGNER S.Wake simulation for wind turbines with a free，prescribed and hybrid wake method［A］.Proc.10th IEA Symp.On the Aerodynamics of Wind Turbines［C］，Edinburgh，1996:23－28.

［6］IVANELL S，MIKKELSEN R，SØRENSEN J，HENNINGSON D.A stability analysis of the tip vortices of a wind turbine［J］.Wind Energy，2009.

［7］XU G，SANKER L N.Computational study of horizontal axis wind turbines［R］.AIAA Paper 99－0042，1999.

［8］GLAUERT H.Airplane propellers［A］.In Aerodynamics theory［M］.Dover Publication Inc:New York，1963，4(Division L):169－360.

［9］BARTHELMIE R，FOLKERTS，LARSEN G C，et al.Comparison of wake model simulation with offshore wind turbine wake profiles measured by sodar［J］.Journal of Atmospheric and Oceanic Technology，23(7):888-901.

［10］DZUIBINSKI Z，WIENZYSLAW S.Vortex ring state simulation using actuator disc［EB/OL］.http://www.scs－europe.net/conf/ecms2007/ecms2007－cd/ecms2007/ecms2007%20pdf/ese_0121.pdf.

［11］SCHLEZ W，TINDAL A，QUARTON D.GH windfarmer validation report［R］.Bristol:Garrad Hassan and Partners Ltd，2003.

［12］EBERLE W R.Wind flow characteristics in the wake of large wind turbines，Vol I，analytical development［R］.DOE/NASA CR－165380.

［13］贺德馨，等.风工程与工业空气动力学［M］.北京:国防工业出版社，2006.

［14］HELMIS C G，PAPADOPOULOS K H，ASIMAKOPOULOS D N，PAPAGEORGAS P G，SOILEMES A T.An experimental study of the near wake structure of a wind turbine operating over complex terrain［J］.Solar Energy，1995，54(6):413-28.