大迎角非定常气动力建模方法研究

孙海生，张海酉，刘志涛

(1.西北工业大学，陕西西安 710072;2.中国空气动力研究与发展中心低速所，四川绵阳 622662)

0 引言

飞机过失速机动时产生的流动分离和旋涡破碎，使得气动力和气动力矩呈现高度的非线性和非定常特性，过失速机动引起的气动力迟滞效应突出。如何精确地确定非定常气动力，对分析飞机的飞行品质和飞行控制系统设计有着极其重要的意义。

风洞试验仍是研究飞机过失速机动非定常气动力的主要手段，但由于条件限制，风洞试验并不能完全模拟飞机大迎角机动飞行中的运动状态。因此，基于风洞试验获得典型机动飞行状态的非定常气动力，通过辨识方法建立非定常气动力数学模型，将气动力和飞行状态直接结合起来，对于飞机过失速机动能力评估和飞行控制律设计具有重要的意义。

经过国内外研究人员几十年的努力，非定常气动力建模取得了重要进展，建立了各种各样的模型，具有代表性的有代数多项式模型、微积分模型和基于现代人工智能的模糊逻辑模型等。这些模型各有优缺点，也有在特殊条件下的成功应用，但是到目前为止仍然没有一种被普遍接受具有较强工程应用价值的非定常建模方法。

本文以SDM标模大振幅俯仰振荡风洞试验数据为基础，建立了几种典型的非定常气动力数学模型，包括基于Fourier变换法的非定常气动力模型、非线性代数模型、基于微分方法的状态空间模型和差分方程模型以及基于人工智能的模糊逻辑数学模型。利用风洞试验数据开展了模型结构辨识和参数辨识，对所建立的几种非定常气动力数学模型进行了比较研究。

1 非定常气动力建模

1.1 代数多项式数学模型

lIN G F等人建立了一种基于线性代数模型的非定常气动力数学模型:非线性代数模型［1］。该模型本质上是利用Taylor级数将气动力和力矩系数表示为飞行状态变量的高阶多项式，模型结构简单，参数辨识容易。以俯仰振荡为例:将纵向气动力和力矩表示成迎角α及其变化率的多项式:

式中Ca表示气动力和力矩系数，例如CL、CD和Cm。一般情况下常数项和只含有α的项的系数取为:

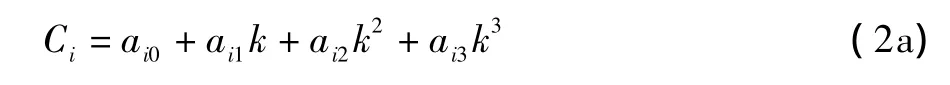
式中，k为减缩频率。利用SDM标模俯仰振荡风洞试验数据进行模型参数辨识。减缩频率范围为0.02667、0.04016、0.05355、0.0667，平衡迎角 α0=40°，振幅 αm=20°。图1给出了建模结果与试验结果的比较。

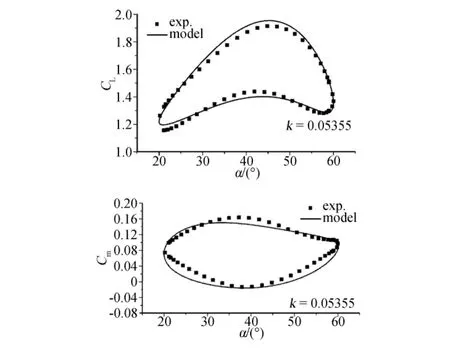
图1 代数多项式模型建模结果与试验数据的比较Fig.1 Comparison of polynomial modeling and test results

1.2 Fourier函数分析模型

C.Edward Lan等人在Tobak和Schiff建立的积分形式的气动力系数表达式基础上利用Fourier分析原理建立了非定常气动力响应模型［2］，以升力为例:

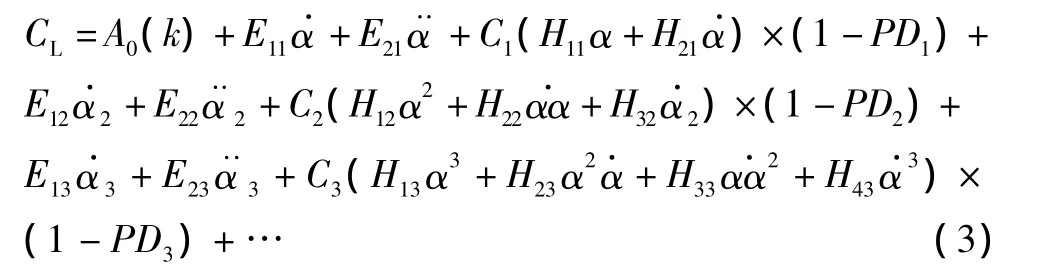
其中，PDj为2阶Padé近似，定义为:

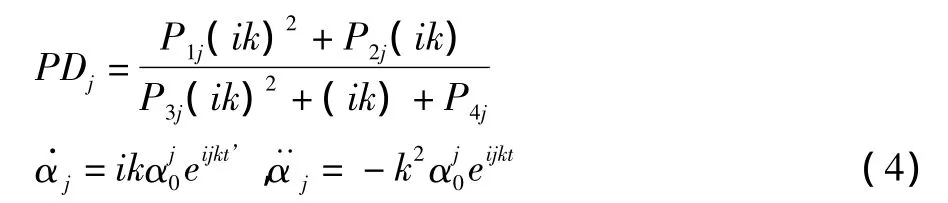
式中，(Eij+Emn)等表示的是附加质量的影响，而(Hijα+Hmn)等为幅值函数，代表的是准定常气动力响应，(1－PDj)为相位函数，表示非定常气动力迟滞，t'为无量纲时间变量。阻力气动力响应模型和俯仰力矩气动力响应模型与式(3)的表达式相同。

首先利用最小二乘法确定系数 P1j、P2j、P3j、P4j，再利用共轭梯度法优化系数E、H。建模结果见图2。

从图2中可以看出，在曲线两端无试验数据处，建模结果出现了振荡。原因是Fourier分析针对数据总体进行分析，在局部区域内基本上无精度可言，针对该问题文献［3］发展了用于局部分析的小波分析建模法。

1.3 状态空间模型

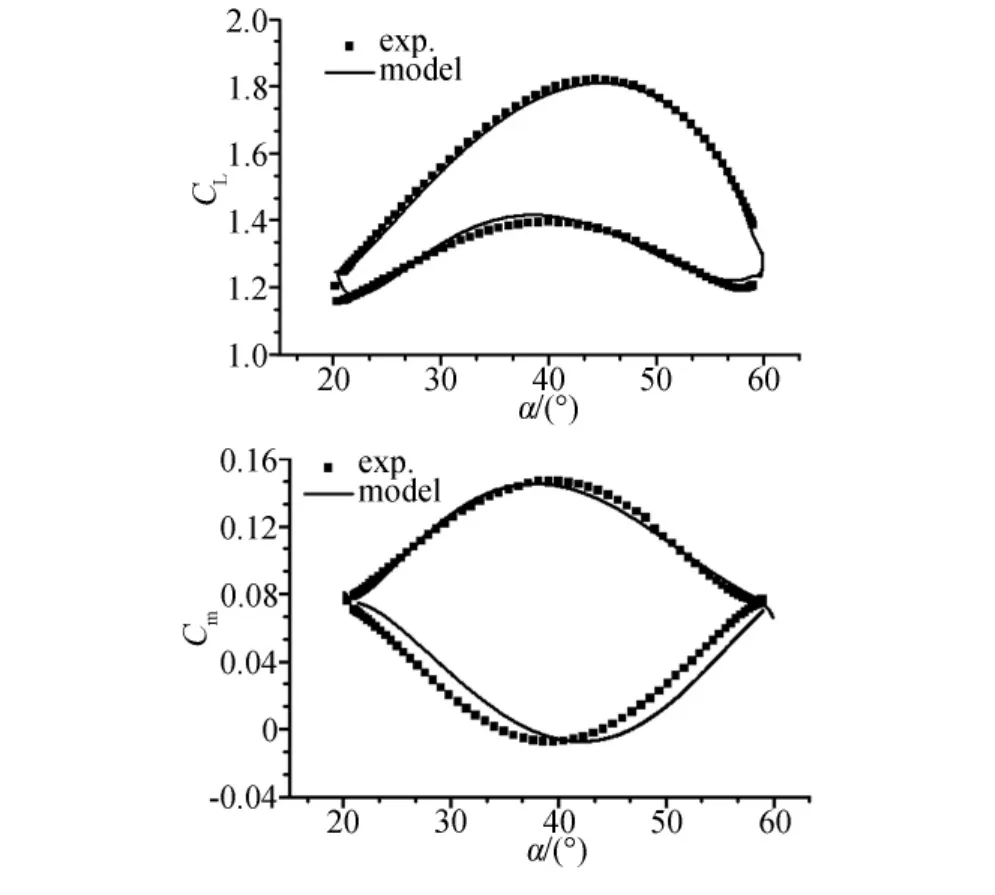
图2 Fourier模型建模结果与试验数据的比较(k=0.04016)Fig.2 Comparison of Fourier modeling and test results(k=0.04016)

状态空间模型是近年来广泛使用的一种非定常气动力模型，它利用微分方程将空气动力载荷和物理流动现象结合在一起，在非定常气动载荷研究方面具有巨大的优势。该方法首先由Goman等人在其1994年发表的著作中将其应用于大迎角非定常气动特性研究。其基本假设是:飞行器大迎角气动力的迟滞效应主要是由流动分离和涡破碎引起的，因此可用与流动分离和涡破碎位置相关的状态变量来描述。引入无量纲量=x/c∈［0，1］描述机翼上表面气流分离点的位置，x表示分离点位置到机翼前缘的距离，c表示翼型的弦长［4］。=1对应于附着流=0对应于分离点在机翼前缘的流动。

典型的大迎角非定常气动力的状态空间数学模型为:

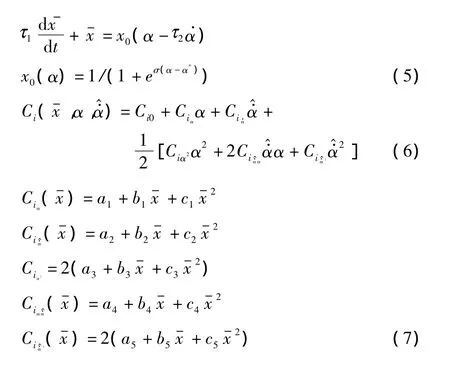
式中，Ci0为常数表征非定常分离过程的时间常数表征分离滞后的时间常数，函数x0(α)表征定常流动状态下分离点坐标和迎角之间的关系;α*对应于分离点位置到达翼型弦线中点时的迎角，σ代表斜率因子=是无量纲化的俯仰角速率，t*=c/2v代表流动的特征时间。

未知参数σ、α*可利用静态试验数据辨识得到、通过非定常试验数据辨识得到。建模结果见图3。

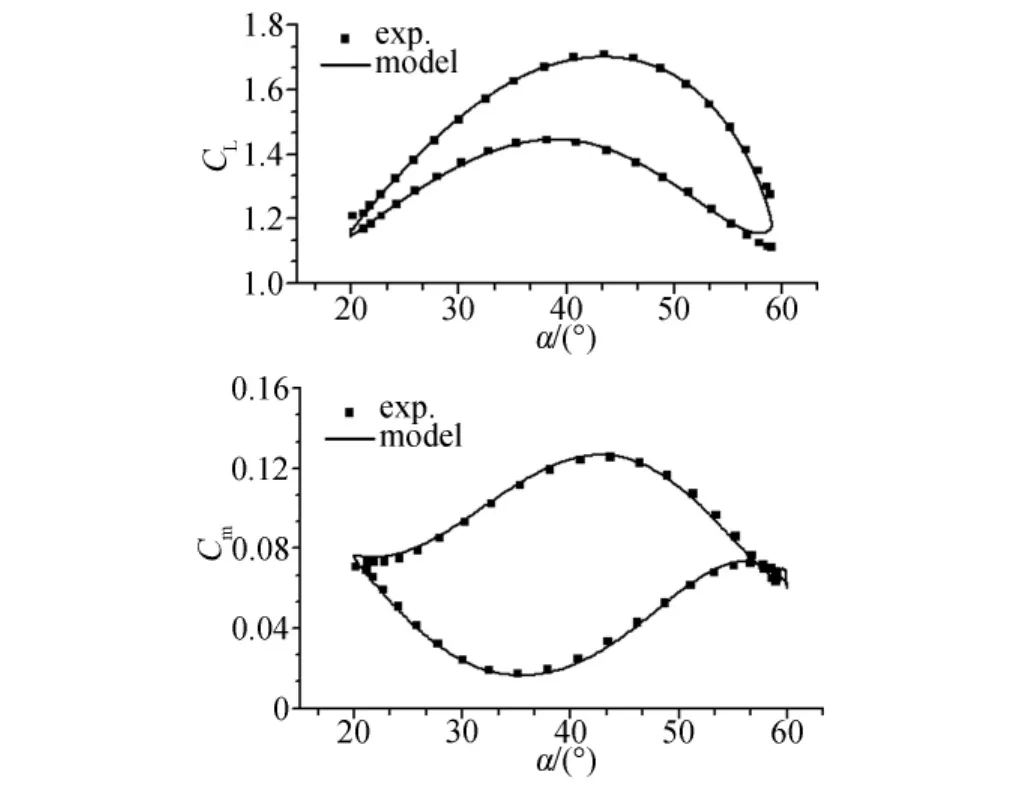
图3 状态空间模型建模结果与试验数据的比较(k=0.02066)Fig.3 Comparison of state space modeling and test results(k=0.02066)

1.4 差分方程模型

在利用状态空间模型建模过程中，状态方程关于分离点位置参数是非线性的，且气动力是状态变量的非线性函数，给模型结构辨识和参数辨识带来很大困难。为克服该问题，汪清等人在文献［5］中提出了一种对气动力系数直接微分的数学模型，模型中各个参数有比较明确的物理意义。

在大迎角条件下，将气动力分解为三部分:静态气动力分量Cist(t)、由定常旋转和下洗迟滞产生的准定常气动力增量Ciqst(t)、由旋涡破裂和恢复迟滞引起的非定常气动力增量Ciunst(t)，其中Ciunst(t)由微分方程表达。用向前差分求解微分方程得到如下结果:

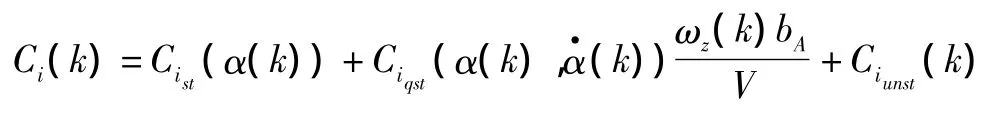
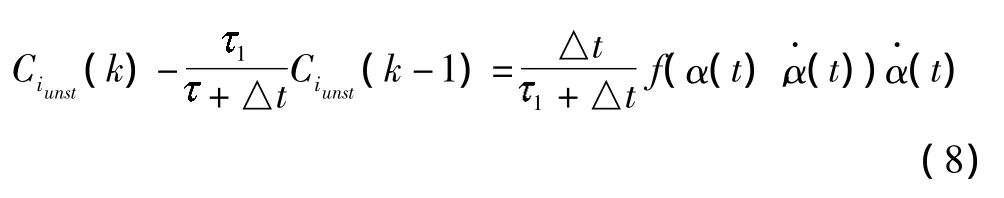
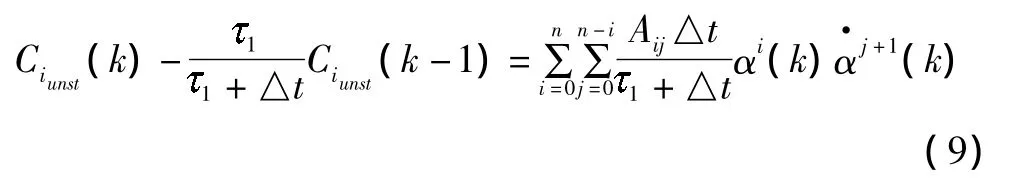
式中，Ci(k)表示非定常试验数据，Cist(k)表示静态气动力系数，可以从风洞静态试验获得，α(k)、(k)通过试验给出;Ciqst(t)可从动导数风洞试验等强迫振动试验中获得。方程(9)变为仅关于2、Aij的线性函数，可利用风洞试验数据通过最小二乘法参数辨识给出估计值。

由式(8)可得，当前时刻的非定常气动力增量Cyunst取决于前一时刻的Ciunst(k－1)和当前时刻的迎角α(k)及其变化率(k)。Ciunst(k)通过Ciunst(k－1)与之前的运动发生联系，明确了该模型的物理意义。

结合式(8)和式(9)可知，每一步计算得到的非定常气动力Ciunst(k)的误差都将传递到下一步，误差的累积最终将影响建模结果的准确性，因此需要对计算结果进行误差修正，本文在建模过程中采用了变系数的高斯白噪声修正。图4给出了微分方程建模结果。

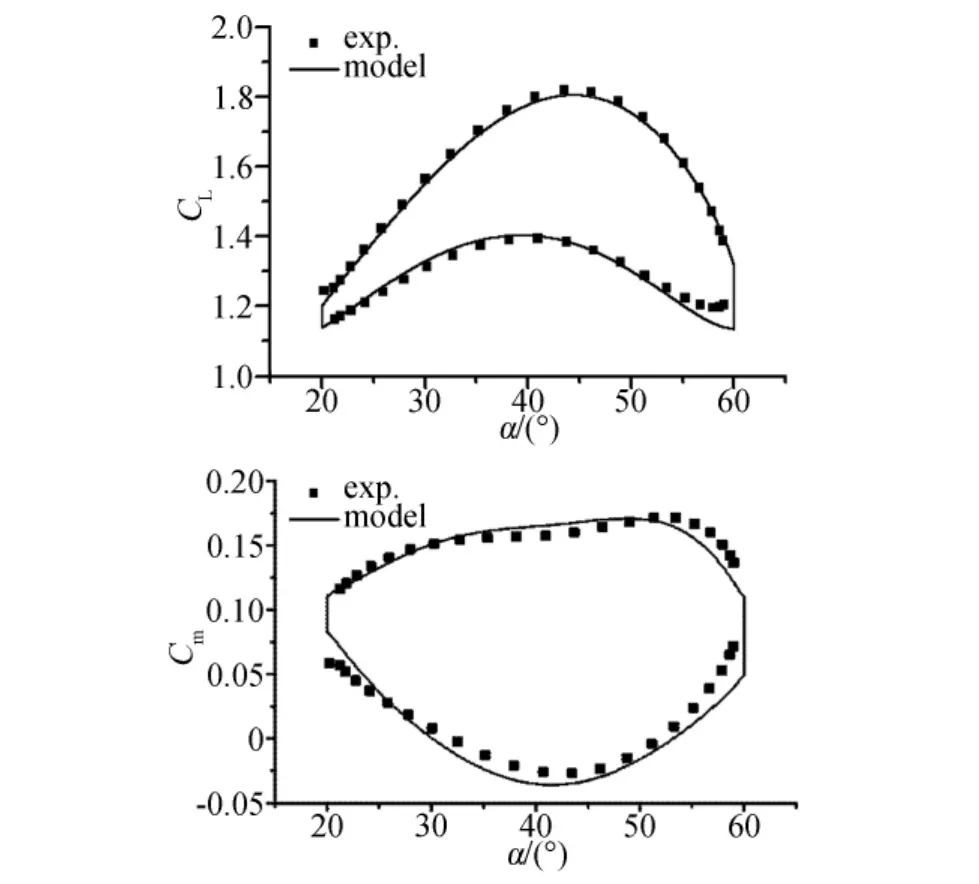
图4 差分方程模型建模结果与试验数据的比较(k=0.02066)Fig.4 Comparison of difference equation modeling and test results(k=0.02066)

1.5 模糊逻辑模型

基于人工智能的模型逻辑和神经网络建模法具有变量多、自学习能力强、精度高等优点，近年来在飞行器非定常气动力建模方面得到广泛应用。

模糊逻辑模型主要包含四个元素:隶属函数、内部函数、模糊规则和输出函数。隶属函数的确定有多种方式，本文采用分析推理法中的三角型隶属函数。

隶属函数把输入空间分成若干个模糊子空间，对每一个变量子空间取一个隶属函数就构成一个模糊单元，内部函数即为模糊单元的输出:

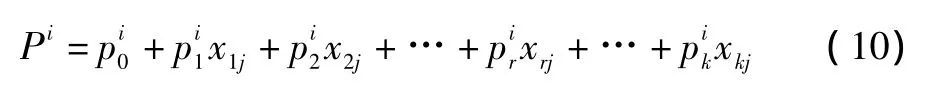
其中，Pi是内部函数)是内部函数的系数，k 为输入变量的个数，(x1j，…，xrj，…，xkj)为第 j个输入样本。

模糊逻辑模型的输出函数为:

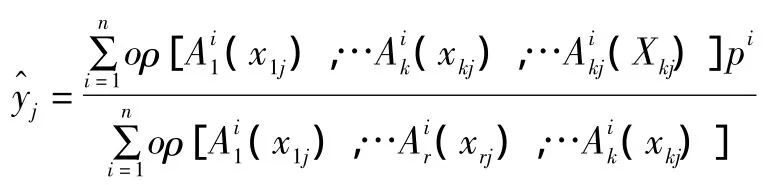
式中，xrj(r=1，…，k)是模型的输入是模型的输出，)是 xrj的隶属函数;(xkj)］表示对第i个内部函数的加权，可以采用隶属函数的乘积运算或取最小运算，本文采用的是取乘积运算;下标j表示第j个输入样本。

图5分别给出了k=0.04016时CL、Cm的模型输出与试验样本的比较。由图可知，二者具有较好的一致性。

图6给出了模糊逻辑模型预测结果与试验结果的比较。由图可知，模糊逻辑模型能较好地预测非定常气动力。

2 建模结果对比

图7为Fourier模型、代数多项式模型、差分方程模型、状态空间模型和模糊逻辑模型辨识得到的SDM标模大振幅振荡时的升力和阻力响应。由图可知在迎角较大时，Fourier模型和差分方程模型的误差较大，建模精度较其它模型差。

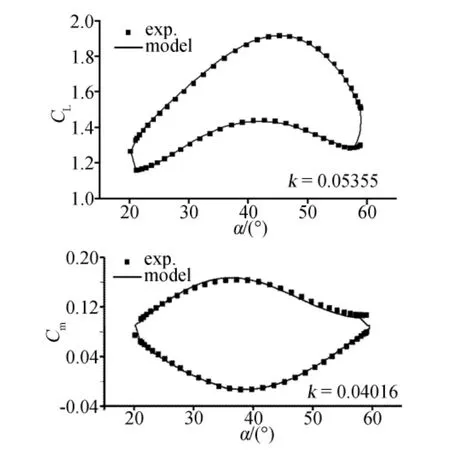
图6 模糊逻辑模型预测结果与试验结果的比较(k=0.05355)Fig.6 Comparison of fuzzy logic predicting and training data(k=0.05355)

从建模过程可知，Fourier模型有明确的表达式，表达式中各项物理意义明确，但模型待辨识参数较多，参数辨识困难，常用于定速率或简谐振荡风洞试验数据建模中。

非线性代数多项式模型表达式简洁，便于应用，但对于不同的试验模型必须建立不同的表达式，多用于运动方式简单，影响参数较少的非定常气动力建模中。

图7 五种不同模型建模结果对比Fig.7 Comparison of the five approaches modeling results

差分方程模型在实际应用中比较方便，但是其累积误差的修正比较困难，对其建模精度有较大影响，该模型多用于静、动态风洞试验数据比较完整的气动力建模中，对飞机的气动性能研究和流动机理研究具有重大意义。

状态空间模型物理意义明确，通用性较强，精度也较高，是近年来应用较多的模型，特别适用于翼型动态特性建模。

模糊逻辑模型虽然没有明确的表达式，辨识出的参数也没有明确的物理意义，但其建模精度最高，可满足多变量气动力的建模需要，具有广泛的应用价值，特别适用于耦合运动、影响参数较多的非定常气动力建模中，对各参数影响程度的研究具有重大意义。

3 结论

通过以上分析，可以得出以下结论:

(1)不同的建模方法各有优缺点，在应用过程中，应根据实际需求进行取舍。

(2)加强对大迎角非定常流动机理研究对于建立物理意义明确、变量多、预测精度高的非定常气动力模型具有重要的意义。

［1］LIN G F，LAN C E.A generalized aerodynamic coefficient model for fight dynamics application［R］.AIAA-97-3643，1997.

［2］CHIN C S，LAN C E.Fourier function analysis for unsteady aerodynamic modeling［R］.N91-18064/6/XAD，1991.

［3］彭小刚.飞行器气动力系数小波网络建模研究［D］.哈尔滨工业大学，2006.

［4］GOMAN M，KHRABROV A.State-space representation of aerodynamic characteristic of an aircraft at high angle of attack［R］.AIAA 92-4651，1992.

［5］汪清.飞机大迎角非定常气动力建模及应用研究［D］.西北工业大学，1994.

［6］孔轶男.气动力建模的模糊逻辑方法［D］.中国空气动力研究与发展中心研究生部，2005.