钝后缘翼型的后缘减阻装置研究

宋 科，李 栋

(翼型、叶栅空气动力学国防科技重点实验室，西北工业大学，西安 710072)

0 引言

关于钝后缘翼型的早期研究发现，其底部附近存在定常或周期性低压流动，带来相当大的底部阻力，所以亚声速翼型设计通常会避免钝后缘的出现［1］。然而近年来，在国外的风电新能源领域中，大厚度钝后缘翼型［2－3］被用于风力发电机叶片。此类翼型相对厚度通常在25%～40%之间，后缘底部相对厚度非常大，通常在10%以上，有的甚至超过20%。它们具有以下特点:

1)结构效率高(结构容积大，容易加工制造);

2)升力特性好(最大升力高，失速迎角大);

3)对表面污染不敏感

其中关于第三点，现有的研究表明［4－5］，通过加厚后缘，将最大相对厚度与后缘相对厚度之差限制在25%以内，有助于降低升力特性对转捩的敏感度。这样风机在运转过程中即使受到灰尘、鸟粪、雨水的沾染，转捩位置和气动特性也不会出现剧烈变化。

气动与结构特性方面的优点使钝后缘翼型非常适合用于大型、超大型风力机叶片。然而钝后缘翼型存在底阻大这一固有缺点，过高的阻力对扭矩和功率输出均有不可忽视的负面影响，探索一种简单实用的钝后缘翼型减阻方法对高性能风机翼型与叶片设计有重要意义。

1 后缘减阻装置

产生底部阻力的主要机理是:流动在底部台阶转角处加速，使压力下降并生成低压旋涡结构，从而产生较大压力差。最近几年国外文献提出［6－7］，在钝后缘风机翼型或叶片后缘安装隔板、锯齿板、空腔等装置，可以削弱后缘的低压旋涡结构，从而实现减小底部阻力的目的。其中隔板是结构最简单的一种装置，为贯通展向的平板(见图1)，其作用是在后缘分隔翼型上下表面的剪切层，抑制低压旋涡的生成，起到减小底阻的作用。

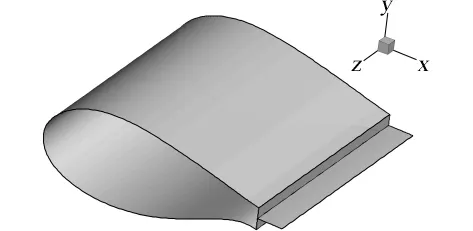
图1 后缘隔板Fig.1 The splitter at trailing edge

2 计算模型

本文研究了FB系列新概念风机翼型［5］中的两个翼型FB-4000-1000与 FBv4000v2000(图2)，最大相对厚度同为40%，后缘厚度分别为10%与20%。该系列翼型主要通过对尖锐后缘基准翼型的后部修形而得到。

本文对比了三种减阻隔板(图3)，分别位于后缘台阶中部、上部与下部，记为“mid”、“up”、“down”。隔板长度等于后缘厚度(本文第4节会解释其原因)，对FB-4000-1000翼型，长度为10%翼型弦长;而对FB-4000-2000翼型，长度为20%翼型弦长。

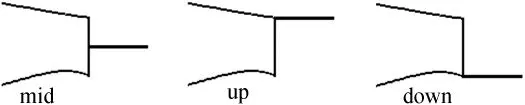
图3 三种隔板布局Fig.3 Three types of splitters

3 数值方法与计算网格

本文求解非定常RANS方程，数值模拟了翼型的粘性绕流。数值方法采用成熟可靠的技术:有限体积离散，二阶精度ROE-FDS格式，双时间推进，LU-SGS子迭代，S-A湍流模型。计算网格采用O型，无隔板网格为401×113，有隔板网格为569×113。附面层第一层网格平均高度约为弦长的0.7×10－5倍，在基于弦长雷诺数为1×106的情况下，y+≤1。图4为FB-4000-1000翼型无隔板情况与带有中部隔板时的后缘附近网格对比示意图。

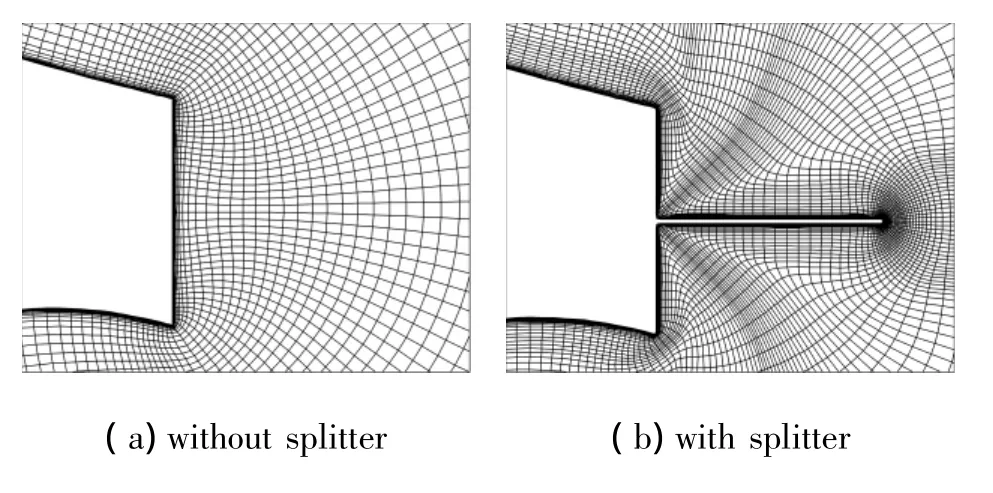
图4 后缘处计算网格Fig.4 The grid at trailing edge

4 计算与分析

FB-4000-1000与FB-4000-2000翼型的计算状态同为 Re=1 ×106(基于弦长)，Ma=0.1405，翼型上下表面固定转捩位置均为5%弦长。首先计算了翼型未安装隔板时的升阻特性，考虑到钝后缘附近因旋涡脱落而出现周期性流动，本文所有算例均采用非定常计算，力系数为平均值。计算结果与文献［5］中的两组计算数据符合良好(图5，其中MSES与ARC2D为参考文献计算值)，验证了本文所使用数值方法的适用性。

图5 FB-4000-1000翼型力系数(无隔板)Fig.5 Force coefficient of FB-4000-1000 airfoil without splitter

后缘减阻隔板安装在台阶中部的情况，已有文献进行了研究，而安装在上部与下部的情况暂未发现相关报导。为了便于对比，本文研究以中部隔板为重点，其数值计算结果(图6、图7)说明，后缘台阶中部安装隔板对两个翼型的影响规律基本一致，并且与文献［6］等的结论相符合:

1)线性段(迎角 －2.5°～5°)升力小幅度下降;

2)失速迎角稍有减小;

3)非线性段(迎角5°～15°)升力与最大升力减小;

4)极曲线低阻区的等升力对应阻力明显降低。

图6 FB-4000-1000翼型力系数(三类隔板)Fig.6 Force coefficient of FB-4000-1000 airfoil with three types of splitter

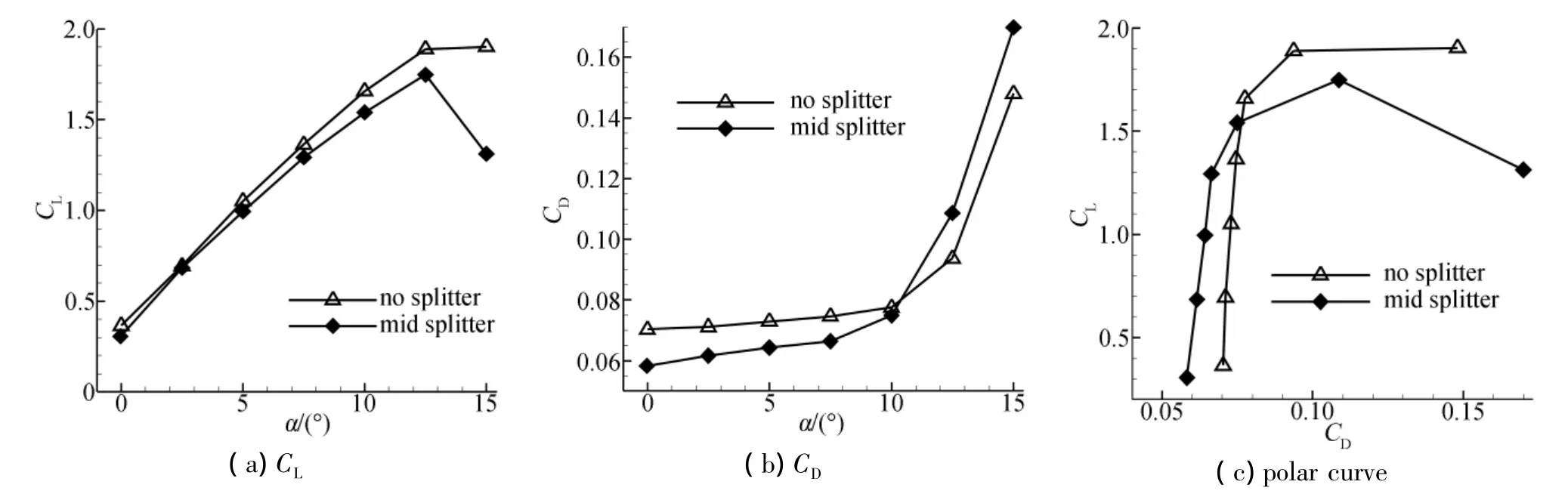
图7 FB-4000-2000翼型力系数(中部隔板)Fig.7 Force coefficient of FB-4000-2000 airfoil with“mid”splitter

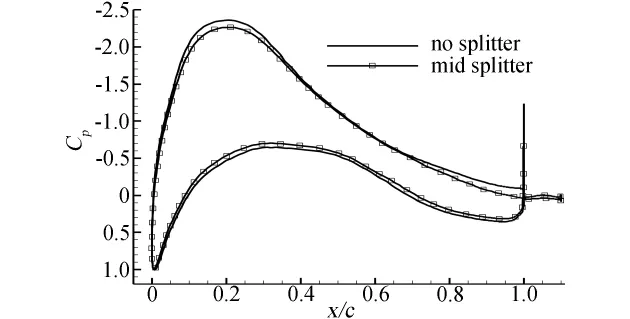
图8 FB-4000-1000翼型压力系数，迎角5°Fig.8 Cpof FB-4000-1000 airfoil，attack angle 5°

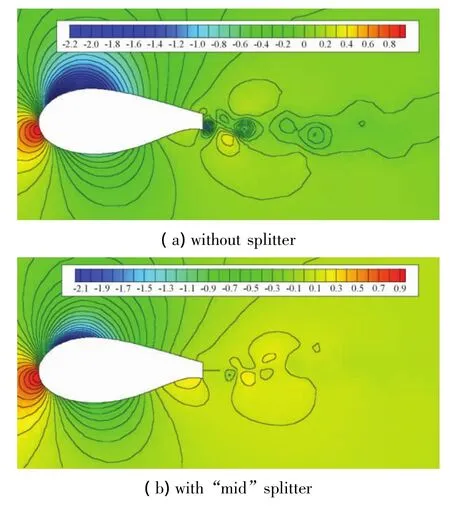
图9 FB-4000-1000翼型压力系数等值线，迎角5°Fig.9 Cpcontour of FB-4000-1000 airfoil，attack angle 5°

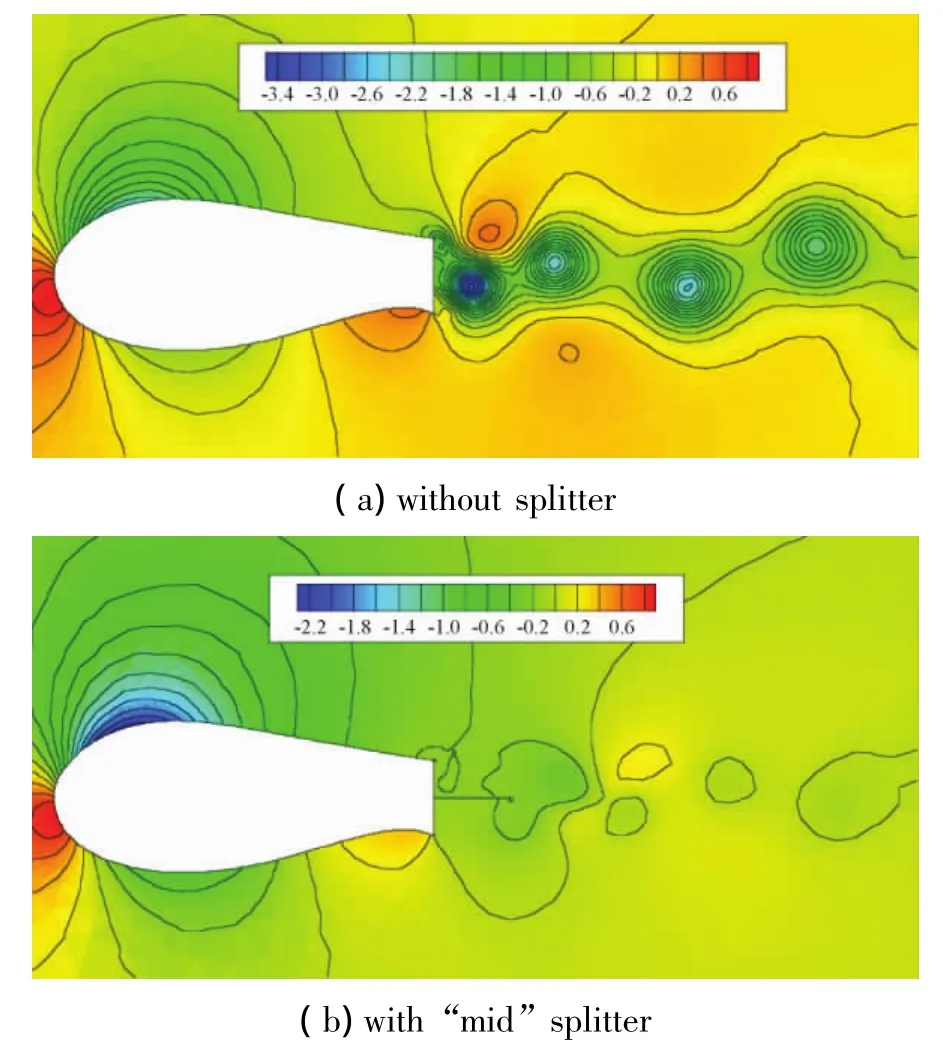
图10 FB-4000-2000翼型压力系数等值线，迎角5°Fig.10 Cpcontour of FB-4000-2000 airfoil，attack angle 5°

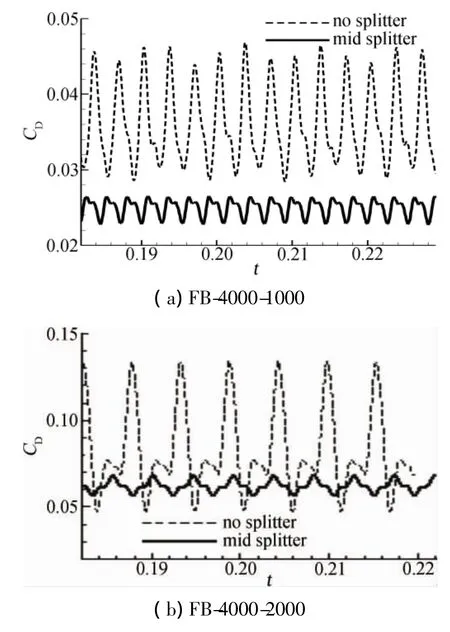
图11 阻力系数脉动曲线，迎角5°Fig.11 The periodic CD，attack angle 5°

关于隔板安装位置的影响，本文进行了对比分析。对于FB-4000-1000翼型(图6)，上下两种隔板都在升力线性段有减阻作用，但效果弱于中部隔板。上部隔板使升力线整体向下移动，升力损失严重，不是合理可行的减阻方式。下部隔板使线性段升力略有提高，而非线性段升力基本不变。表1显示了各迎角对应的减阻百分比，中部隔板的效果最好，在中小迎角范围内减阻29%～36%，平均约35%;大迎角时平均也超过20%。

以上研究中，隔板长度选取为等于后缘厚度，是由于以下原因:(1)隔板等后缘减阻装置通过改变后缘台阶处的旋涡流动，减小负压值，从而实现减阻。后缘的大尺度旋涡流动，受制于几何外形边界条件，其特征长度与后缘厚度相当。本文认为如果要对后缘大尺度流动产生显著影响，隔板长度应达到此特征长度，即后缘厚度。隔板长度太小则不足以产生足够影响作用。例如FB-4000-1000翼型中部隔板布局，通过数值计算(图12)验证了隔板长度等于50%后缘厚度时，其减阻效果较差。

(2)后缘隔板需要通过收放机构实现打开与闭合，如图13，上部隔板紧贴翼型后缘端面，以铰链A为转轴打开;而中部隔板由两段折叠而成，每段长度均等于后缘厚度的一半，先以铰链A为转轴打开90°，再将外段隔板以B为转轴打开180°。对于中部隔板的情况，如果长度超过后缘厚度，隔板就需要3段以上折叠结构，如果长度超过2倍后缘厚度，则上部与下部隔板也将不得不采用3段结构，结构重量增加，结构刚性难以保证。

综合气动与结构两方面因素，本文认为隔板长度益取为等于后缘厚度。

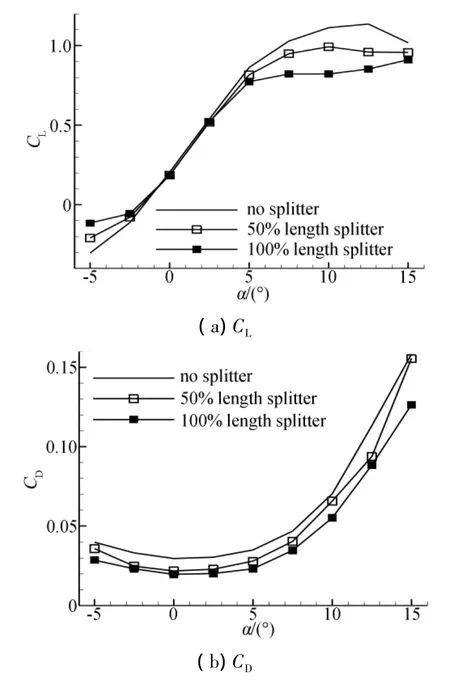
图12 FB-4000-1000翼型力系数(不同长度的中部隔板)Fig.12 Force coefficient of FB-4000-1000 airfoil with“mid”splitter of different length

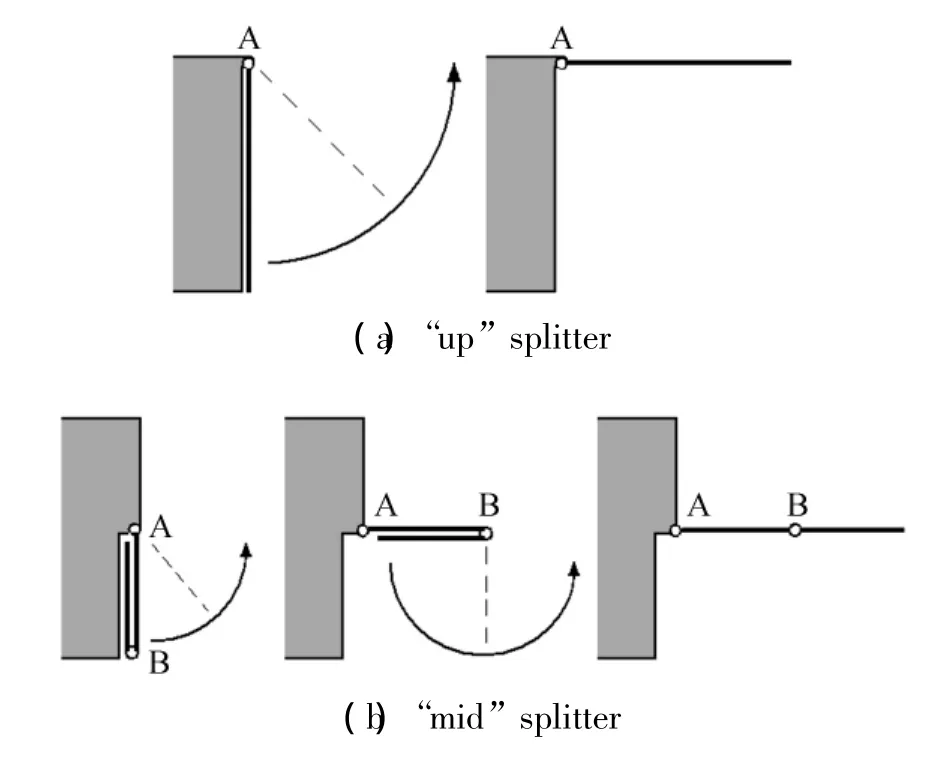
图13 隔板收放机构示意图Fig.13 Opening/closing device of splitters

5 总结

后缘隔板三种布局中，上部隔板布局因升力损失严重而使综合气动性能恶化;下部隔板布局虽然减阻效果稍弱，但因其升力几乎没有损失而具有一定实用价值;中部隔板布局以一定程度升力损失为代价减阻20%以上，特别是中小迎角线性段升力损失较少，如果只考虑此迎角范围，减阻效果相当显著，平均约35%。综合分析可知，中部与下部隔板是具有发展潜力的两个减阻方案，两者的对比也给出一种提示:隔板安装在后缘台阶中部偏下的位置，有可能获得更好的综合减阻效果。今后将尝试通过数值优化方法找出给定工况下最优的减阻隔板安装位置，并进一步探索其他形式后缘减阻装置。

［1］NASH J.A review of research on two-dimensional base flow［J］.Aeronautical Research Council，1963，3323.

［2］TPI Composites.Innovative design approaches for large wind turbine blades［R］.SANDIA Report 2003-0723.

［3］TPI Composites.Innovative design approaches for large wind turbine blades final report［R］.SANDIA Report 2004-0074.

［4］STANDISH K J，VAN DAM C P.Aerodynamic analysis of blunt trailing edge airfoils［J］.Journal of Solar Energy Engineering，2003，125:479-487.

［5］VAN DAM C P，MAYDA E A，CHAO D D，BERG D E.Computational design and analysis of flatback airfoil wind tunnel experiment［R］.SANDIA Report 2008-1782.

［6］JONATHON P B ，VAN DAM C P.Drag reduction of blunt trailing-edge airfoils［A］.International Colloquium on:Bluff Bodies Aerodynamics ＆ Applications［C］.Italy，July，2008.

［7］VAN DAM C P，KAHN D L，BERG D E.Trailing edge modifications for flatback airfoils［R］.SANDIA Report 2008-1781.