高前进比旋翼气动特性分析方法研究

孔卫红，陈仁良

(南京航空航天大学 直升机旋翼动力学国家级重点实验室，江苏南京 210016)

0 引言

常规直升机由于前行桨叶的激波和后行桨叶的气流分离，速度受到很大限制。由常规直升机加装机翼并用推进装置替代尾桨所形成的复合式直升机(如图1)被认为是未来提高直升机飞行速度的有效途径之一。这种直升机在悬停和低速时以直升机模式工作，随着飞行速度的增加，旋翼转速逐渐降低，旋翼载荷逐渐减小，升力逐步由机翼承载，而推力则由相应的推力装置来提供，当速度提高到一定值后，固定翼飞机的飞行模式成为复合式高速直升机的主要飞行模式，使飞行速度得到大幅度提高［1－6］。

图1 复合式高速直升机Fig.1 Compound helicopter

复合式直升机在高速飞行时，旋翼的前进比可高达0.8［7］，远高于常规直升机旋翼的前进比，后行桨叶大部分处于反流区内，气流分离现象更严重，前行桨叶的压缩效应更突出，偏流作用很显著。上述现象使桨叶剖面的迎角变化范围很大，引起桨叶和旋翼的气动力在旋转一周的过程中发生很大的变化，直接导致桨叶非定常挥舞运动及随时间变化的旋翼诱导速度，这种非定常的挥舞运动和诱导速度反过来又影响到桨叶剖面的迎角变化及桨叶和旋翼气动力的变化，形成复杂的耦合关系，常规直升机旋翼的理论不适用。

准确预测高前进比的旋翼气动特性是当前复合式高速直升机面临的技术难题之一。McCloud J L和Charles B D对高前进比旋翼的气动特性进行了风洞试验研究，得到了H－34旋翼和UH－1D旋翼在前进比高达0.86 时的旋翼气动特性风洞试验数据［8－9］。Wayne Johnson和Prouty对常规直升机旋翼后行桨叶的反流区问题进行了探讨［10－11］，其中仍然沿用了小迎角范围的翼型升力线理论和叶素积分法，并采用均匀诱导速度假设，由于常规直升机的反流区面积比很小，用这种方法分析得到的气动特性对计算结果的影响很小，但高前进比旋翼的反流区面积比例很大，用此方法来分析其气动特性与实际情况出入较大。Hyeonsoo Yeo和Wayne Johnson［7］用CAMRAD II软件分析了复合式高速直升机高前进比旋翼的气动特性，并用风洞试验数据进行对比验证，但对反流区内的桨叶阻力系数采取人为添加常数的方法，限制了方法的通用性。

本文根据高前进比旋翼前行桨叶压缩性、后行桨叶失速效应严重以及桨叶偏流作用和反流区显著增大的特点，提出了高前进比旋翼气动特性的分析方法以及与之相适应的桨叶剖面阻力系数随前进比和桨叶气动载荷的变化规律。建立了高前进比旋翼的桨叶非定常挥舞运动模型与诱导速度时变非均布模型。然后根据旋翼气动力、桨叶挥舞运动和旋翼诱导速度三者之间的内在耦合关系提出了高前进比旋翼气动特性的动态响应计算方法，最后以H－34旋翼为例，分析计算了高前进比状态的气动特性，并用风洞试验数据［8］验证计算结果的合理性。

1 高前进比旋翼的气动特性分析方法

1.1 高前进比旋翼气动力模型

为了细致描述高前进比旋翼桨叶不同位置的迎角，本文首先对桨叶进行离散，然后根据桨叶微段安装角和气流速度确定桨叶各剖面的迎角。对高前进比旋翼，桨叶上的偏流效应很大，对实际迎角有影响，考虑偏流效应的桨叶微段迎角为:

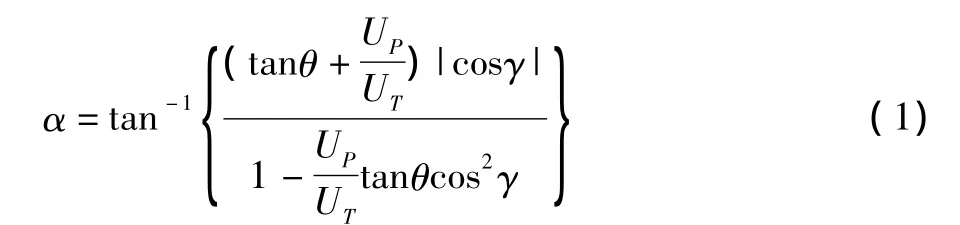
其中

γ为偏流角。

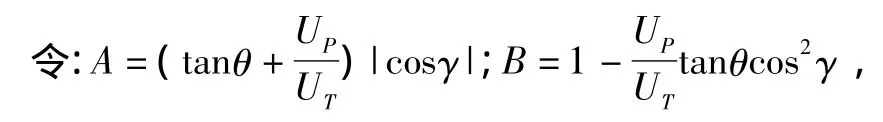
则根据A、B的不同取值，桨叶剖面迎角存在以下几种情况:

1)B=0，A=0，则 α =0°

2)B=0，A ＞0，则 α =90°

3)B=0，A ＜0，则 α = －90°

4)B ＞0，则 α =tan－1(A/B)

5)B ＜0，A ＞0，则 α =tan－1(A/B)+180°

6)B ＜0，A ＜0，则 α =tan－1(A/B)－180°

其中当迎角是5)或者6)的情况时，表明桨叶微段处在反流区内。

式(1)中的θ由自动倾斜器运动引起的操纵量(总距、纵横向周期变距)、变距挥舞耦合、桨叶几何负扭转以及桨叶动态扭转变形引起的桨距变化量来确定，即:

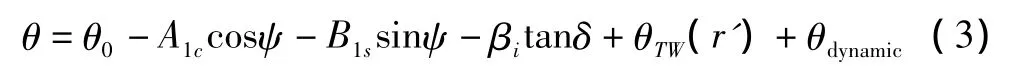
其中θdynamic为桨叶动态扭转变形引起的桨距变化量，由经验公式［12］得到:

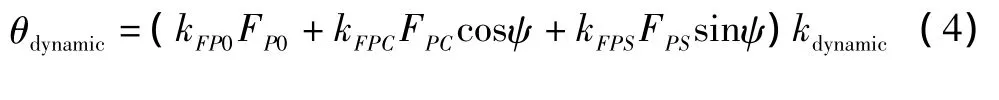
式中，kFP0、kFPC、kFPS、kdynamic为经验系数，FP0、FPC、FPS由下式确定:

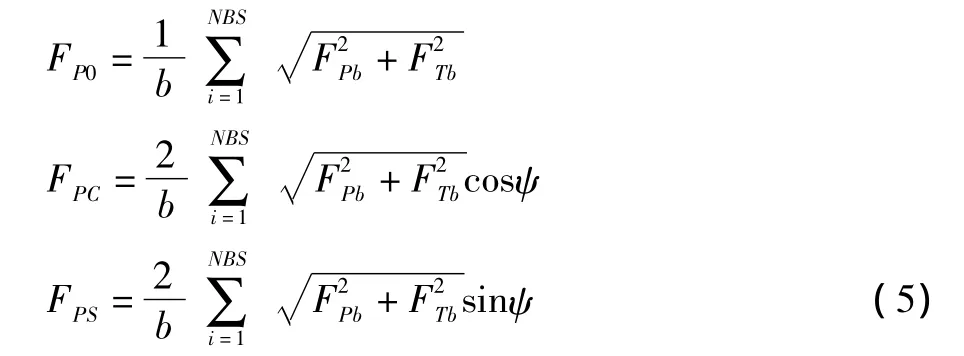
FPb、FTb为水平铰处的垂向和切向力，NBS为桨叶片数。

桨叶上任一点的速度不仅取决于来流旋翼速度μxs、μzs(μxs为旋翼桨毂平面处的来流速度，μzs为垂直旋翼桨毂平面的来流速度)、桨叶挥舞速度、旋翼旋转速度Ω、同时还与旋翼尾迹在桨盘处的诱导速度v有关，其沿桨叶展向和垂向分别为 － vsinβi、－ vcosβi，其中βi为第i片桨叶的挥舞角。

桨叶微段气流速度的无量纲形式为:

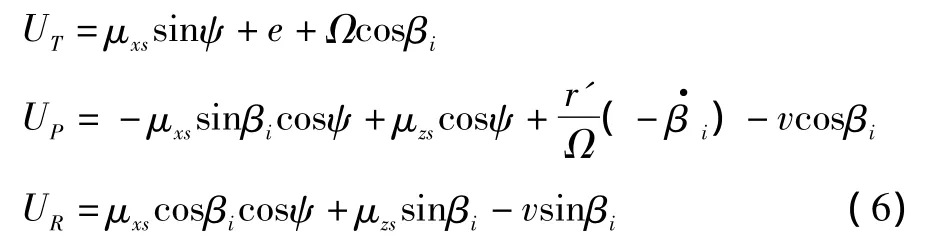
根据桨叶剖面的实际迎角，结合翼型风洞试验数据(0～1.0的马赫数及±180°迎角所对应的升力和阻力系数)可得到桨叶微段的升力和阻力系数:

式中:

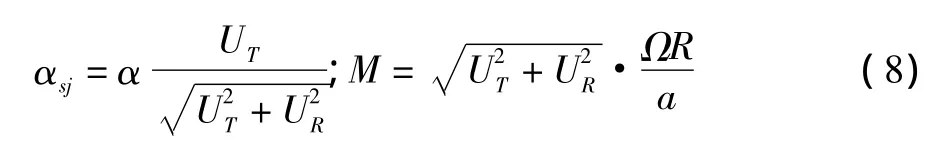
由于实际桨叶的偏流会延缓失速期间附面层的分离，能提高翼型的最大升力系数，故在桨叶剖面的升力系数也应考虑偏流效应，这样桨叶微段上垂向、切向、和展向的气动力分别为:

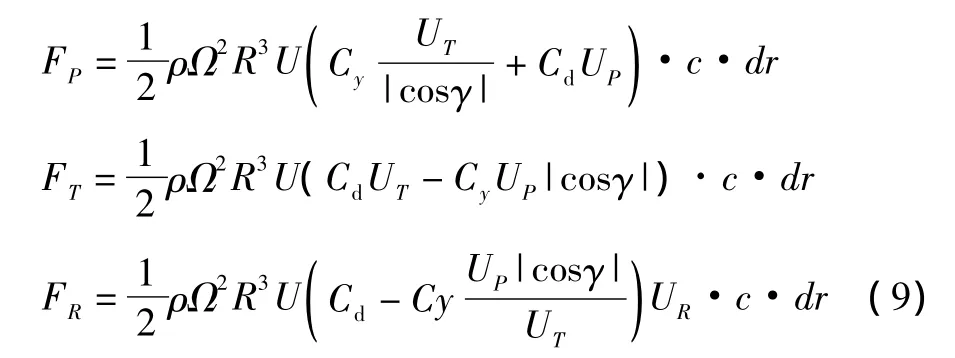
对桨叶各微段气动力求和，可得桨叶垂向、切向和展向的气动力:

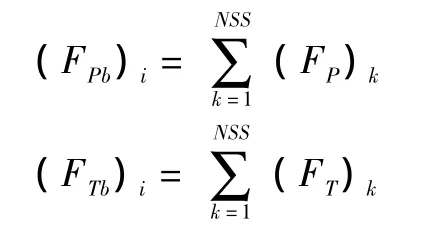
上述气动力模型能反映桨叶不同剖面和方位处的压缩性、失速特性、偏流效应及处在反流区内的桨叶非线性气动力。

将各片桨叶气动力转换到旋转轴系，并考虑桨叶非定常运动引起的惯性载荷，可得各片桨叶在旋转轴系下的载荷为:

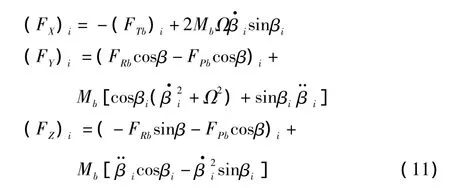
由此可得旋翼非定常载荷为:

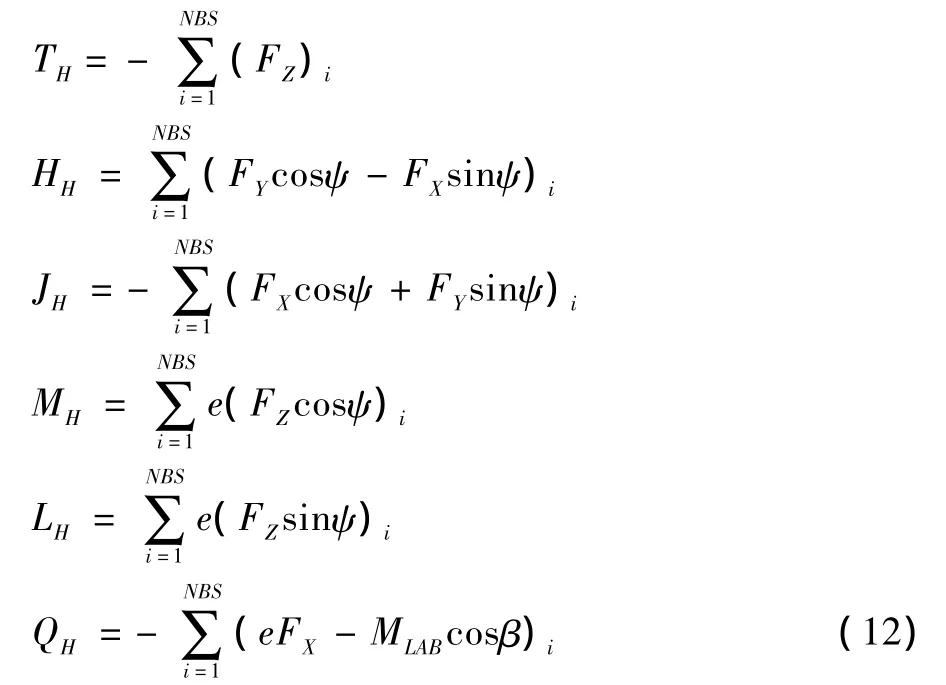
式中(MLAB)i为桨叶气动力对摆振铰力矩之和。

高前进比旋翼的后行桨叶迎角很大，有的部位严重失速，在旋转一周的过程中是一种动态失速过程，动态失速会使旋翼桨叶剖面的阻力显著增加。由于目前尚缺少有关高前进比旋翼动态失速的风洞试验数据，理论分析方法也不成熟，本文通过修正式(7)中的旋翼桨叶剖面阻力系数来反映高前进比旋翼的动态失速。即:

其中k为考虑动态失速对阻力系数的修正因子，很显然，该因子与旋翼前进比和桨叶载荷有关，经过大量试算和分析，最终得到:

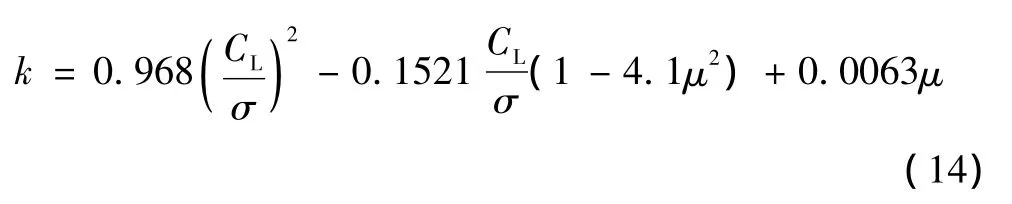
至此，可得高前进比旋翼的拉力系数和功率系数分别为:

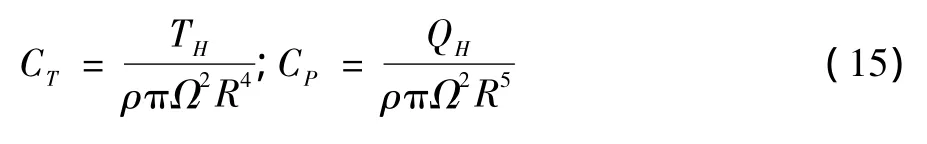
1.2 桨叶非定常挥舞运动模型

桨叶的挥舞运动，与桨叶气动力之间的关系十分密切，当桨叶气动力变化时，桨叶的挥舞运动经历动态响应过程，而桨叶挥舞运动反过来又会影响到各片桨叶的气动力及旋翼诱导速度。

对常规直升机的旋翼来说，桨叶的挥舞运动采用桨盘平面法获得，即用桨盘锥度角、后倒角和侧倒角来描述旋翼桨叶的挥舞运动。但是当旋翼工作在高前进比状态时，桨叶上作用的气动力和惯性力均处于较大幅度的变化之中，桨盘平面法不适合描述高前进比旋翼的挥舞运动，需从各片桨叶的运动入手，确定任意时刻或任意方位的桨叶挥舞运动。

根据作用在桨叶上的空气动力、离心力、挥舞惯性力、约束弹簧力及桨叶重力(较小可忽略)等绕挥舞铰产生的力矩的动态平衡关系，可得桨叶的挥舞运动方程:

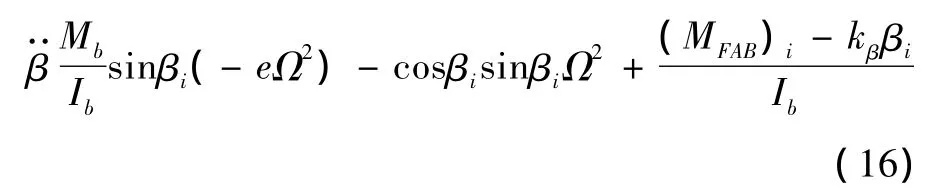
式中(MFAB)i为桨叶气动力对挥舞铰力矩之和。

设在时刻t(对应的方位角为ψt)其桨叶的挥舞角、挥舞速度和挥舞加速度分别为，经过△t后(对应的方位角为ψt+1)上述三个量的值分别为，当△t很小时有下列式子:

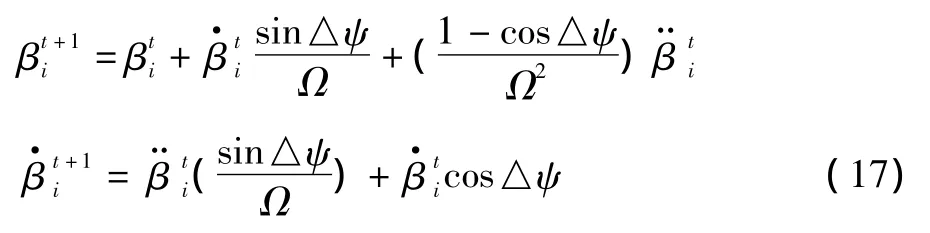
将式(16)与式(17)联立，即可得到挥舞运动的递推公式:

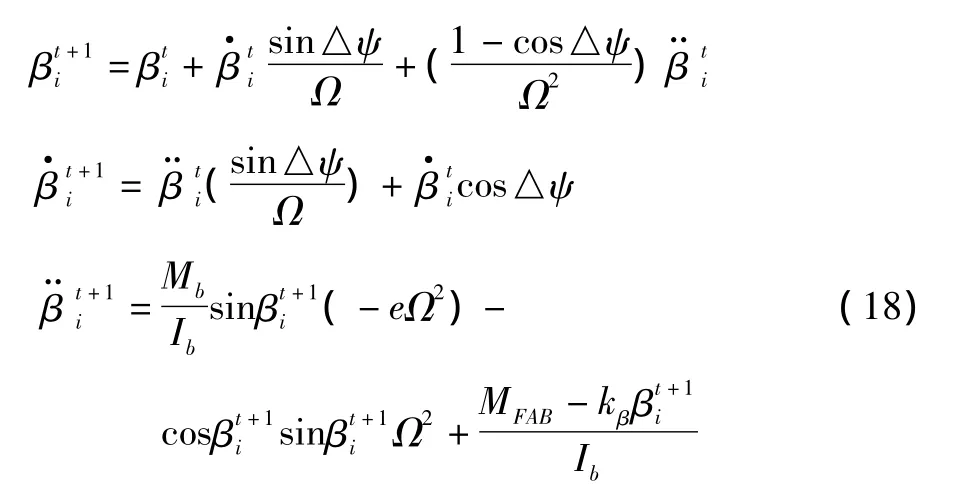
上述挥舞方程是在旋转轴系中得到的，表示任一片桨叶在旋转过程中的挥舞运动。要研究整个旋翼的挥舞情况，则应将旋转轴系的挥舞量转换到不旋转轴系。而旋转轴系下的挥舞值与不旋转轴系下的值之间有下列关系:

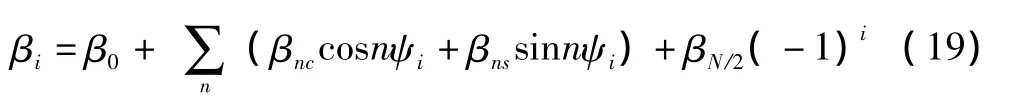
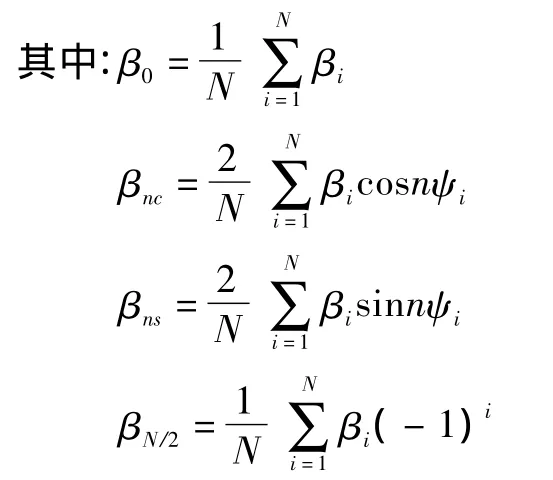
当旋翼挥舞达到动态稳定，各片桨叶具有相同轨迹，其中一阶谐波运动为前面提到的桨盘平面及旋翼锥体概念，即β0表示旋翼的锥度角，β1c、β1s表示后倒角和侧倒角，而βnc、βns(n＞1)表示桨叶相对于旋翼锥体的高阶谐波运动。很显然，此时的旋翼挥舞运动锥面不再均匀光滑，这也是高前进比旋翼挥舞运动的特点。

1.3 时变非均布诱导速度模型

由于高前进比旋翼的反流区面积占整个旋翼面积的比例相当大，而反流区内升力很小，甚至是负升力，诱导速度在桨盘上的分布更不均匀，且随旋翼气动力变化而变化，变化的诱导速度又通过对桨叶剖面气动力的影响而影响着旋翼的气动力及桨叶的挥舞运动。

实践证明，Pitt和Peters的一阶谐波动态入流模型比较适合桨叶载荷的精确分析，它考虑了诱导速度在桨盘上的不均匀分布，以及随旋翼气动力变化的滞后效应，使旋翼气动载荷(拉力、滚转力矩和俯仰力矩)同旋翼的诱导速度的瞬态变化联系起来，适合高前进比旋翼诱导速度的计算。

取旋翼尾迹在桨盘处的诱导速度的一阶谐波分布形式:

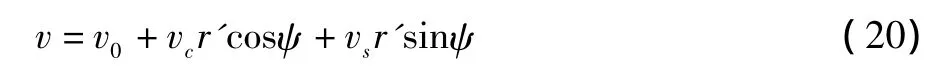
则反映时变非均布诱导速度的系数v0、vc、vs可表示为:

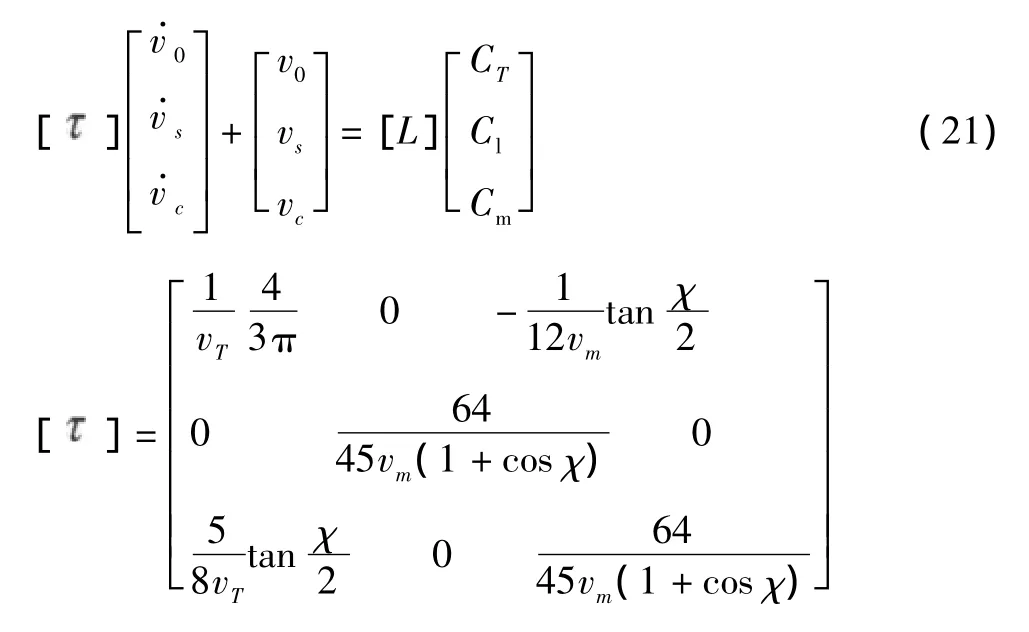
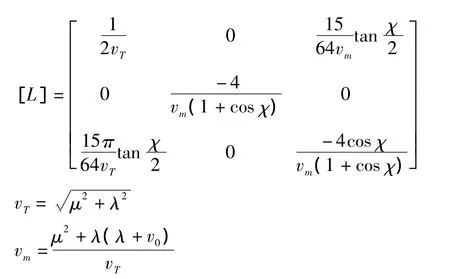
式中χ是旋翼尾迹偏斜角，CT、Cm、Cl分别是旋翼的拉力系数、俯仰力矩系数和滚转力矩系数。

1.4 高前进比旋翼气动特性的动态响应计算

从以上分析可以看出，对于给定的运动状态，高前进比旋翼的气动力中包含了桨叶的非定常挥舞运动和旋翼的时变诱导速度，同样桨叶的挥舞运动包含了桨叶的气动力和旋翼的时变诱导速度，旋翼的时变诱导速度包含了旋翼的气动力和桨叶的非定常挥舞运动。旋翼气动力、挥舞运动和诱导速度三者之间相互影响、相互作用，构成图2所示的闭环系统。

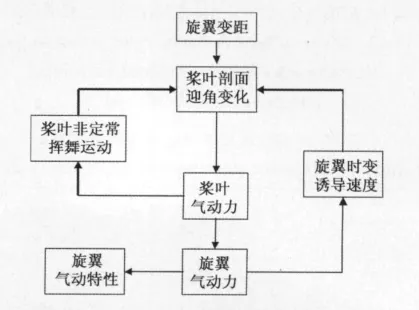
图2 高前进比旋翼气动力、挥舞运动及诱导速度的关系Fig.2 Relationship among rotor aerodynamic force，flap motion and induced velocity

很显然，高前进比旋翼气动特性应是旋翼的诱导速度、桨叶的挥舞运动和旋翼气动力三者都达到动态平衡之后得到的结果。针对上述耦合特点，本文提出一种计算高前进比旋翼气动特性的动态响应方法，图3为该方法的计算流程图。

2 旋翼气动特性模型的验证与分析

为了验证前面所述高前进比旋翼气动特性分析方法的合理性，本文以H－34旋翼为例进行气动特性计算，该旋翼为4片桨叶无扭铰接式旋翼，半径8.53m，弦长0.41m，本文根据文献［8］的试验状态计算该旋翼不同前进比和迎角组合(如表1所示)时的气动特性。

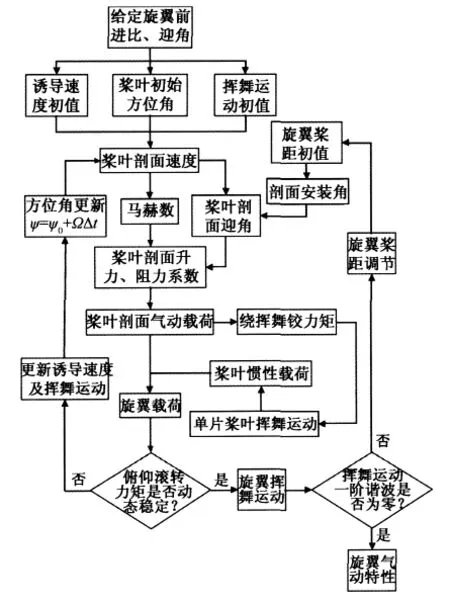
图3 高前进比旋翼气动特性动态响应计算流程图Fig.3 Diagram for calculating rotor aerodynamic characteristics at high advanced ratio with dynamic response method

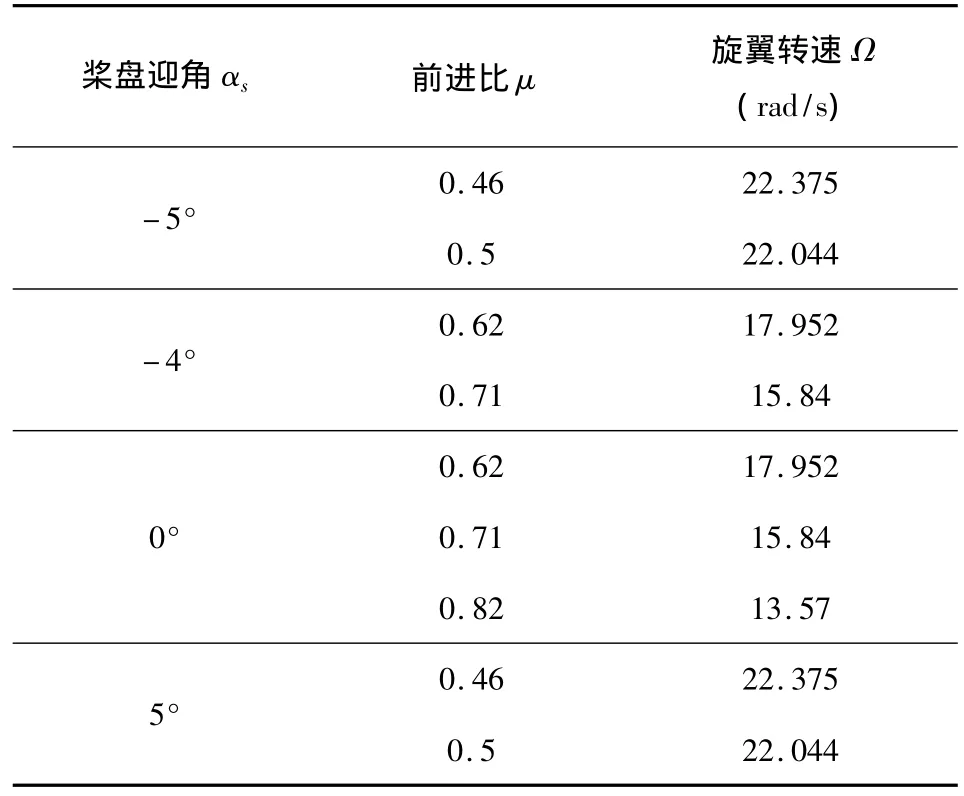
表1 高前进比旋翼气动特性计算状态Table 1 States for rotor performance calculation

图4给出了H－34旋翼在不同前进比和迎角组合情况下的气动特性计算结果及相应的风洞试验结果［8］。为了便于与风洞试验结果进行对比，图中纵坐标为旋翼诱导功率与型阻功率之和，横坐标为由旋翼拉力、后向力和侧向力形成的总升力。

从图中可以看出，计算结果与风洞试验数据吻合得较好，表明本文所述方法合理。

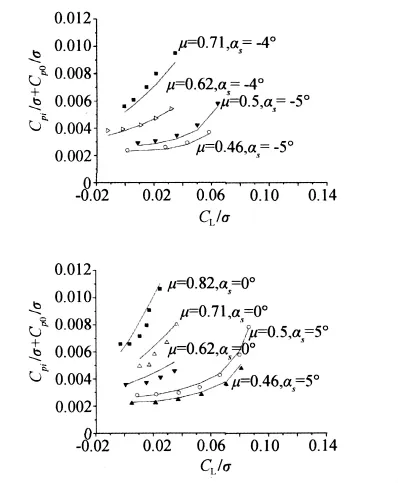
图4 H-34旋翼高前进比性能计算结果与试验数据的对比Fig.4 Comparison between measured and predicted performance for H-34 rotor at high advanced ratio

3 结论

本文针对高前进比旋翼的特点建立了适合高前进比旋翼的气动特性模型，该模型能合理反映桨叶不同剖面和方位处的压缩性、失速特性、偏流效应以及处于反流区内的桨叶气动载荷，提出了高前进比旋翼桨叶剖面阻力系数随前进比和桨叶气动载荷的变化规律，提高了高前进比旋翼气动特性模型的精度。

建立了与高前进比旋翼的气动特性模型相匹配的诱导速度时变非均布模型与桨叶非定常挥舞运动模型，根据旋翼气动力、旋翼诱导速度和桨叶挥舞运动三者之间的内在耦合关系提出了高前进比旋翼气动特性的动态响应计算方法，并通过计算结果与试验数据的对比验证了所建模型的合理性。

［1］BÜHLER M，NEWMAN S J.The aerodynamics of the compound helicopter configuration［J］.The Aeronautical Journal of the Royal Aeronautical Society，1996，100(994):111-120.

［2］NEWMAN S J.The compound helicopter configuration and the helicopter speed trap［J］.Aircraft Engineering and Aerospace Technology，1997，69(5):407-413.

［3］ORCHARD M N，NEWMAN S J.The compound helicopter－Why have we not succeeded before?［J］.The Aeronautical Journal ofthe RoyalAeronauticalSociety， 1999， 103(1028):489-495.

［4］HORN J F，GEIGER B R，PIASECKI F W，GREENJACK A.Trim and maneuver optimization methods for a compound rotorcraft［A］.Proceedings of the 60th Annual Forum of the American Helicopter Society［C］.June，2004.

［5］GEIGER B R.Flight control optimization on a fully compounded helicopter with redundant control effectors［D］.The Pennsylvania State University，May，2005.

［6］SWARTZWELDER M A.Trim and control optimization of a compound helicopter model［D］.The Pennsylvania State U－niversity，August，2003.

［7］YEO H，JOHNSON W.Aeromechanics analysis of a compound helicopter［A］.Presented at the American Helicopter Society 62nd Annual Forum［C］.Phoenix，Arizona，May 9－11，2006.

［8］MCCLOUD J L，BIGGERS J C，STROUB R H.An investigation of full－scale helicopter rotors at high advance ratios and advancing tip Mach numbers［R］.NASA TN D－4632，July，1968.

［9］CHARLES B D，TANNER W H.Wind tunnel investigation of semirigid full－scale rotors operating at high advance ratios［R］.USAAVLABS TR 69－2，January，1969.

［10］JOHNSON W.Helicopter theory［M］.Princeton University Press，1980.

［11］PROUTY R W.Helicopter performance，stability，and control［M］.Wadsworth Pub Co publishers，1986.

［12］HOWLETT.UH－60A Black Hawk engineering simulation program:Volume Ⅰ－Mathematical model［R］.NASA Report.December，1981.