多孔隔热材料内压响应的影响因素分析
2011-11-08程晓丽俞继军姜贵庆
黄 飞,程晓丽,俞继军,姜贵庆
(中国航天空气动力技术研究院,北京 100074)
0 引言
新型高超声速飞行器要经历长时间的气动加热环境,在材料非烧蚀的要求下,对飞行器的隔热性能模拟提出了更高的要求。目前,随着多相复合材料传热机制研究的不断深入,材料的隔热性能也相应的得到大幅度提高。多相隔热材料是利用空气分子在低压下碰撞频率的降低来实现材料整体的良好隔热性能。如当空气足够稀薄时,可以近似认为是不存在传导导热的,因此在材料中引入多空隙结构,并降低组成纤维的尺寸大小,可以有效地提高材料的隔热性能。现有研究结果表明具有多孔结构、密度较低、由纤维或颗粒组成的多相材料在飞行器的隔热设计中具有良好的应用前景,可以有效发挥阻断或者延缓热量传递的功能。
多孔隔热材料存在明显的微纳米高孔隙结构特征(图1),其热导率对压力的响应非常敏感[1],因此了解材料内部压力的响应过程和响应时间,对确定多孔隔热材料的热导率就显得尤为重要,从现有研究手段来看多以实验为主,在某一给定压力环境下测出材料的等效热导率,由于压力响应时间的差异,很难提取响应过程中其随环境压力变化的经验关系式,国内外许多学者开展了相关方面的研究工作[2-5],然而将DSMC方法应用于材料内部压力响应方面的研究工作还不多见。
基于此,文中在文献[1]的研究基础上进一步对孔隙率、纤维尺寸、较大的宏观尺寸等影响因素进行了深入分析,研究了纤维尺寸 1.25μm、2.5μm、10μm,孔隙率85%、90%、95%,内外压比,以及模型的宏观尺寸对内部压力响应时间的影响,为材料的隔热机理研究提供理论基础。
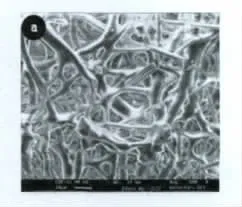
图1 多孔隔热材料的微观结构Fig.1 Micromechanism of multiphase thermal insulation material
1 计算方法-DSMC方法
1.1 计算方法介绍:
DSMC[6]方法的基本思想是:用有限个仿真分子代替真实气体分子,并在计算机中存储仿真分子的位置坐标、速度分量以及内能,其值随仿真分子的运动、与边界的作用以及仿真分子之间的碰撞而改变,最后通过统计网格内仿真分子的运动状态实现对真实气体流动问题的模拟。计算时除考虑平动能外,还考虑了内部能量。作为近似,分子的内能只考虑转动能,未考虑振动能。分子间相互作用模型采用VHS模型,物面边界条件采用完全漫反射条件,平动能与内能的能量交换采用L-B模型[7-8],按照Bird的能量按自由度分配原则采用取舍法进行抽样分配[8]。
本文根据材料特征对材料的模化网格进行随机地选择标注来区分纤维和孔隙,运用改进后的DSMC程序对标记为实心的网格面进行物面的漫反射处理,其它的处理方法与传统DSMC方法一致。主要模拟步骤如下:
1)选取纤维的平均尺寸作为网格的尺寸,以孔隙率为标准对网格进行随机地选择标注,其中标注网格1、0来区分纤维与孔隙,并用数组对每一网格的1、0标注信息进行记录。
2)对于标注为0的孔隙网格布置粒子,采用DSMC方法进行分子的碰撞运动模拟,其中分子每次运动后对于标注为纤维的网格4个面将视为固体物面,判断分子是否与其碰撞,若分子与其作用将采用物面漫反射处理,反射后将以反射速度继续运动剩余时间。
3)对材料中心点附近的几个网格进行采样统计,可得出压力随时间的响应规律。
1.2 主要关键技术点:
1)分子与物面碰撞点的求法:
分子与物面的碰撞点就是分子与网格面的碰撞点,碰撞点的坐标按照直线(即分子运动轨迹)与平面的交点求解(如图2)。
分子运动前的坐标为(XI,YI,ZI),运动后的坐标为(XI+DX,YI+DY,ZI+DZ),设碰撞点的坐标为(XC,YC,ZC),P为物面网格的基本点,n为物面的法向矢量,n=RI×RJ,RI、RJ是由网格面的顶点所决定的基于P顶点的两个矢量。设物面方程为:
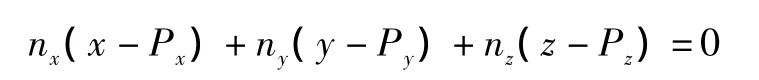
分子运动轨迹的直线方程为:
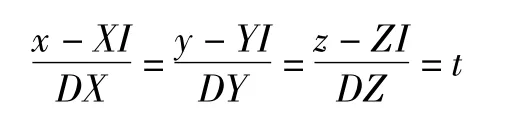
由以上两方程可得到:
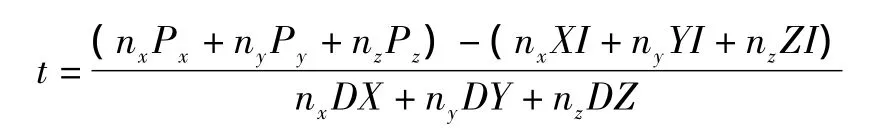
从而可得到碰撞点的坐标为:
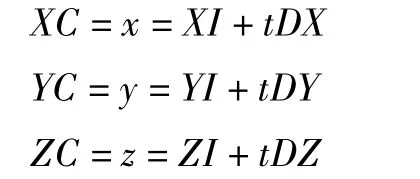
本文为二维问题,只需去掉Z方向的相关量即可。
2)分子与纤维碰撞的判断方法:
由于分子频繁地与周围网格面作用,这对于分子所在网格的判断带来困难,尤其是当分子越过两个网格时的判断更为复杂,在较小时间步长下越过两个以上网格的分子数极少,因此,作为近似,我们对越过两个网格以上的分子进行减速处理不会带来很大误差,而对于越过一个网格的分子进行判断相对容易。将分子运动前所在的网格记为II、JJ,运动后的网格记为ICN、JCN;此时我们可以将分子的判断分为9种情况进行区分判断:
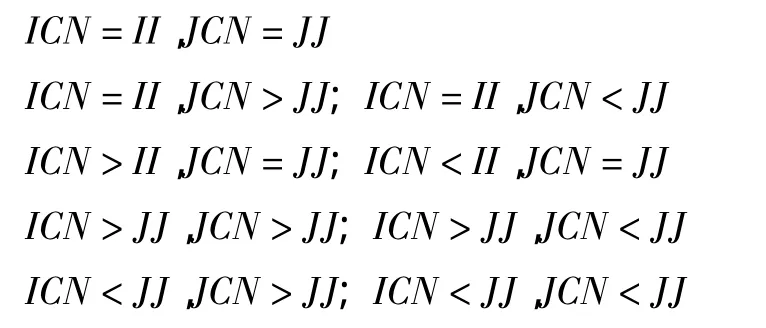
以上所有的情况中只要与网格面相交,求出交点后就需要判断相邻的网格是否标注为纤维(即数组Ibiaozhu为1),是纤维的进行物面反射,反射后将以反射速度继续运动剩余时间,不是纤维时分子将以原速度继续运动剩余时间。
本文程序的算例验证见文献[9]。
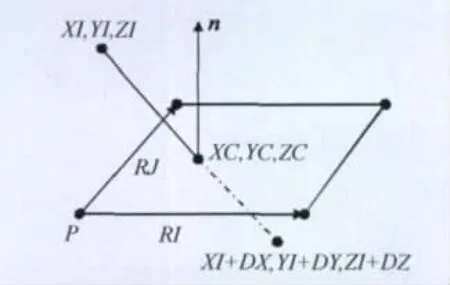
图2 分子碰撞示意图Fig.2 Molecular collision with wall
2 计算结果与分析
2.1 计算状态:
计算的网格示意图如图3,其中网格尺寸采用纤维的近似尺寸,分别选取了 1.25μm、2.5μm、10μm,其中孔隙率选取了85%、90%、95%,在网格中随机地选取相应比例的实心网格作为纤维,选取后的隔热层简化模型如图4,其中黑色的点代表场中的纤维,其余为孔隙结构。宏观尺寸选取了1mm ×1mm、2.5mm×2.5mm、5mm×5mm、10mm ×10mm、20mm ×20mm 等,材料内部的压力 Pin为1Pa、10Pa、100Pa等,外部环境的压力 Pout为 0.1Pa、1Pa、10Pa、0.2Pa、2Pa、20Pa 等。
计算的来流温度T∞为300K,壁面温度Tw为300K,边界AB和BD采用对称边界,AC和CD为自由来流边界条件,即分子可以在四周边界自由进出。纤维物面边界以壁温Tw进行漫反射处理。
2.2 压力的时间响应
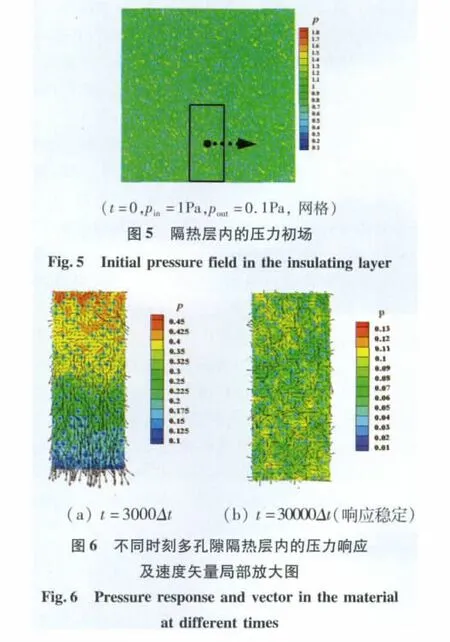
图5为隔热层尺寸在1mm×1mm(网格100×100)时,隔热层的内压为1Pa时的压力初场,其中的实心点代表场中的纤维,场中其余位置布置空气分子,其压力值约为1Pa。图 6中的(a)图和(b)图分别为 t=3000Δt、t=30000Δt时刻图5中所示位置处的压力响应及速度矢量的局部放大图。从t=3000Δt中可以看出,由于内压pin=1Pa大于外压pout=0.1Pa,在这种压力驱动下,气体不断地向周围环境扩散,在隔热层内形成了明显地压力梯度,当t=30000Δt时,内压达到与环境压力基本相等,这种压力梯度随之消失,气体表现为图中随机的扩散运动。
孔隙率效应:
图7给出了在纤维尺寸10μm、宏观尺寸10mm×10mm下,不同孔隙率时的压力响应历程,从图7(a)中可以看出,在内外压力比pin/pout=10时,孔隙率降低,分子运动受到固体纤维的阻挡增强使得响应时间有所增大,在此模拟条件下,孔隙率每降低5%,响应时间约增加了0.002s,响应时间的相对增量较大,从而可知,孔隙率对响应时间的影响较大。图7(b)为内外压比等于5时的响应曲线,其中孔隙率对响应时间的影响规律与图7(a)的规律相似。

图3 网格示意图Fig.3 Grid in the computation region

图4 隔热层二维简化模型Fig.4 Simplified model of insulating material
2.2.2 纤维尺寸效应
图8给出了孔隙率90%时不同宏观尺寸下,纤维尺寸对响应时间的影响规律。从图8(a)中可以发现,在相同的宏观尺寸及孔隙率下,随着纤维尺寸的减小,响应时间增大。这主要是因为,相同孔隙率下,纤维的尺寸越小,代表纤维的网格数越多,纤维面的总面积越大,气体受纤维壁面的阻挡作用越强烈。图中还可看出,在此条件下,响应时间的相对增量较大,响应时间对纤维的尺寸较为敏感。图8(b)对应的宏观尺寸状态下具有与图8(a)中相似的变化规律,仅不同之处在于由于宏观尺寸的增加导致每条曲线的响应时间相对更长。
2.2.3 内外压比效应
图9为纤维尺寸10μm,孔隙率90%,宏观尺寸10mm时不同内外压下的响应曲线。经过厘米量级尺寸的计算,从图9(a)中可看出,即使在较大尺寸下,当尺寸不变时,内外压比相等,响应时间也相等的结论仍然成立,这一结论与文献[5]的结论相同。因此,为了节省计算时间,同样尺寸下,对高压状态下的模拟可以采用低压状态来进行近似模拟。图9(b)中给出了不同压比下的响应曲线。从中可以发现,内外压比增加,压力达到稳态时需要的响应时间将更长,然而,由于压比增加时,气体扩散的速度将有所增加,这在一定程度上又会使降低响应时间有所降低,两种相反的作用使得最终响应时间受内外压比的影响较弱。宏观尺寸效应:
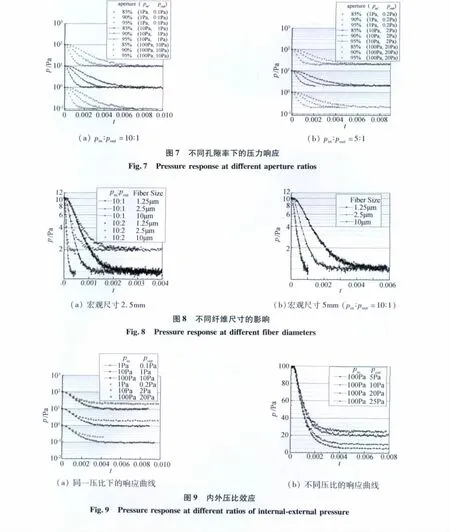
图10为纤维尺寸10μm,孔隙率90%时不同宏观尺寸下压力响应的对数曲线。从图中可以看出,当材料长度增大2倍即面积增大4倍时,响应时间的对数值的增量近似相等。这一结果表明,即使宏观尺寸进一步增加,响应时间的对数值近似呈现线性增加的结论仍然成立,这一结论与文献[5]中小尺寸下的结论相同。
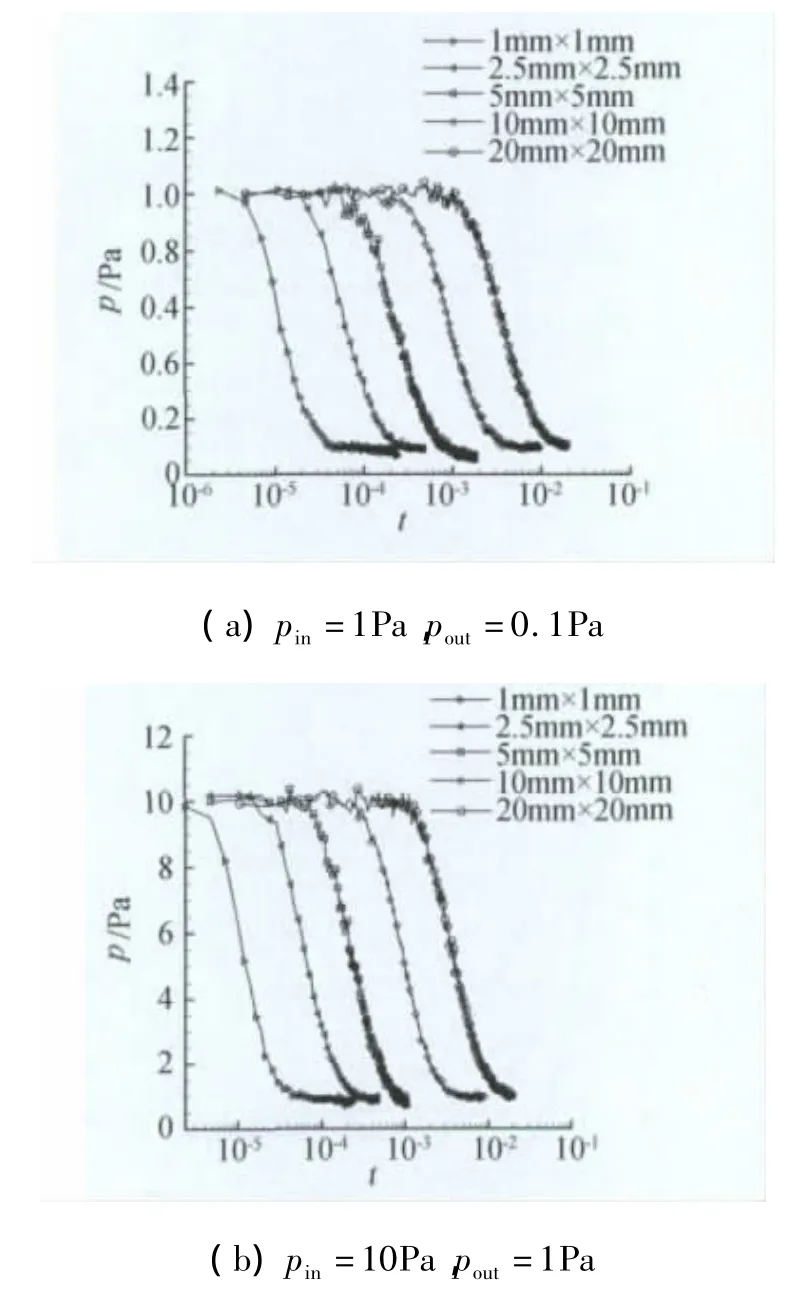
图10 不同宏观尺寸下的压力响应Fig.10 Pressure response at different material thickness
3 结论
基于多孔隔热材料的特征,本文采用文献[5]中建立的模拟手段,进一步选取了 1.25μm、2.5μm、10μm 的纤维尺寸,85%、90%、95%的孔隙率,宏观尺寸达到厘米量级的模拟环境,对影响压力响应的众多因素进行了系统性地分析。结果表明:
(1)孔隙率对响应时间的影响较大,同一条件下,孔隙率减小,响应时间增大。
(2)响应时间对纤维尺寸较为敏感,同一条件下,纤维尺寸降低,响应时间增大。
(3)响应时间对内外压比的敏感性相对较弱,同一条件下,内外压比增加,响应时间有所增加。
(4)即使在较大的宏观尺寸下,当材料长度增大2倍即面积增大4倍时,响应时间的对数值的增量也近似相等,即响应时间的对数值近似呈现线性增加的结论仍然成立,这一结论与文献[5]中小尺寸下的结论相同。
[1]黄飞,程晓丽,俞继军.多孔隙隔热材料内压的时间响应[J].宇航学报,2010,31(1)∶233-238.(HUANG F,CHENG X L,YU J J.The study of pressure respond to time on multiaperture insulating material[J].Journal of Astronautics,2010,31(1)∶233-238.)
[2]MARSCHALL J,MADDREN J.Internal radiation transport and effective thermal conductivity of fibrous ceramic insulation[R].AIAA 2001-2822,2001.
[3]KAMRAN D.Thermal analysis and design of multi-layer insulation for re-entry aerodynamic[R].AIAA 2001-2834,2001.
[4]KAMRAN D.Heat transfer in high-temperature fibrous insulation[R].AIAA 2002-3332,2002.
[5]HANLON M A,MA H B.Evaporation heat transfer in sintered porous media[R].AIAA 2002-3092,2002.
[6]BIRD G A.Molecular gas dynamics and direct simulation of gas flow clarendon[M].Oxford,1994.
[7]BORGANOFF C,LARSEN P S.Statistical collision model for monte carlo simulation of polyatomic gas mixture[J].Journal of Computational Physics,1975,18∶405-420.
[8]陈伟芳,吴其芬.高温稀薄气体热化学非平衡流动的DSMC方法[M].长沙:国防科技大学出版社,1999.(CHEN W F,WU Q F.DSMC method of nonequilibrium thermodynamics and chemical reaction in the high temperature rarefied gas flow[M].Chang Sha:National University of Defense Technology Press,1999.)
[9]黄飞,程晓丽,沈清.高超声速平板近空间气动特性的计算分析研究[J].宇航学报,2009,30(3)∶900-907.(HUANG F,CHENG X L,SHEN Q.Numerical investigation of hypersonic aerodynamics of flat plate flying in near space[J].Journal of Astronautics,2009,30(3)∶900-907.)
