非下采样变换的红外与可见光图像融合

陈小林，王延杰

(中国科学院长春光学精密机械与物理研究所，吉林长春130033)

1 引言

图像融合是一种综合处理多源图像和图像序列的技术，这种技术将来自不同数据源的多特征图像进行合并，得到一个包含被测物体信息更完整的图像，融合后的图像具有比参加融合的任意一幅图像更优越的性质，能更精确地反映客观实际［1］，更适合人的视觉和计算机视觉，或者更适合进一步的计算机图像处理(如图像分割、特征提取、场景监视、目标识别及目标检测等等)的需要［2］。

目前，图像融合技术在军事上的应用越来越广泛，如导弹防御系统、精确制导导弹、自主式炮弹等技术。在民用方面，图像融合也在遥感、智能机器人、医学诊断和材料检验等领域得到相当广泛的应用［3-7］。

小波(Wavelet)变换融合法［10］是目前学术界讨论最广泛的图像融合方法。大部分小波变换融合法中都是采用离散小波变换，也有许多学者也将其他形式的小波变换应用到图像融合中，如平移不变小波、复小波、多小波等。同金字塔变换一样，小波变换也是一种图像的多分辨率分析方法。同金字塔变换不同的是，小波变换具有较好的方向性，而且可以是非冗余的，正交小波变换还可以去除两相邻尺度上图像信息间的相关性。不过，小波变换不能最优地表示含线或者面奇异的高维函数。为了发展出一种新的高维函数的最优表示方法，有人提出将 Ridgelet，Curvelet，二代 Curvelet，Contourlet，非下采样 Contourlet为代表的多尺度几何分析(Multiscale Geometric Analysis)工具［11］用于图像融合。基于其灵活的局部性和方向性，Choi等人率先将Curvelet变换引入到遥感图像融合，之后，很多学者相继将各种多尺度几何分析工具运用到图像融合中，这些方法的基本思路同金字塔变换融合法和小波变换融合法相似。

令人关注的是，CunhaA.L.等人在Contourlet变换的基础上，提出了一种具有平移不变特性的Contourlet变换-非下采样 Contourlet变换(Nonsubsampled Contourlet Transform， NSCT)［12］。NSCT不仅具有多尺度、时频局部特性，还具有多方向特性，能够有效捕捉图像中的几何特征，并且能够对图像进行稀疏表示，变换后能量更加集中，能够为图像融合提供更多的有用信息。图像经NSCT分解得到的各子带图像之间具有相同的尺寸大小，从而便于融合运算的实现。NSCT在离散域中采用滤波器组实现图像的多尺度、多方向分解，因而也有着较快的运算速度。

本文基于非下采样Contourlet变换，针对红外图像与可见光图像的融合，提出了加权与选择结合的图像融合算法，并针对低频子带系数和各带通方向子带系数提出了低频基于区域梯度信息、高频基于区域特征因子的融合方案。实验结果显示，提出的算法具有更高的融合性能。

2 非下采样Contourlet变换

对于一维分段光滑或者有界变差函数，小波分析比傅里叶分析具有更“稀疏”的表示能力。不过小波这种最佳处理“点”奇异性的优势却不能简单地推广到二维或更高维，不能有效处理“线”奇异性或“面”奇异性的信号。主要原因是二维可分离小波基只具有有限的方向，即水平、垂直、对角，方向性的缺乏使小波变换不能充分利用图像本身的几何正则性。

Contourlet变换除了具备时频局部特性，还具备“各向异性”，可以在长宽比随尺度而变化的基支撑区间，每个尺度上不等数的方向分解，从而实现对图像的稀疏表示。在Contourlet变换的基础上，Cunha A.L.等人提出了非下采样Contourlet变 换 (Nonsubsampled Contourlet Transform，NSCT)［12］。

NSCT具有平移不变特性，与Contourlet变换一样，都是分开进行尺度与方向的分解，采用非下采样塔式滤波器组(Nonsubsampled Pyramid Filter Bank，NSPFB)进行多尺度分解，再利用非下采样方向滤波器组(Nonsubsampled Directional Filter Bank，NSDFB)对前面的多尺度子带图像进行方向分解，最终完成图像各个方向尺度的子带分解，如图1所示。

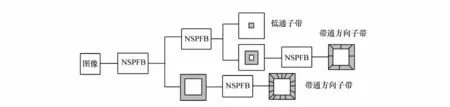
图1 NSCT分解结构示意图Fig.1 Schematic diagram of NSCT breakdown structure

在图像的分解与重构期间，NSCT采取避免降采样和上采样的操作步骤，使得NSCT同时具备了平移不变性和子带图像间的同尺度特性［13，14］。

NSCT采用的NSPFB为二通道非下采样滤波器组，如图2(a)所示。其中，分解滤波器{H0(z)，H1(z)}和合成滤波器{G0(z)，G1(z)}，G(z)满足Bezout恒等式，如式(1)所示，从而保证了NSPFB满足完全重构(Perfect Reconstruction，PR)条件。类似一维“átrous”小波算法，为实现多尺度分解，下级进行上采样时，采样矩阵D=2I(I是2阶单位矩阵)。

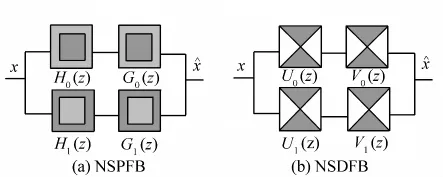
图2 NSCT中二通道非下采样滤波器组Fig.2 Two channel nonsubsampled filter group in the NSCT

图3 给出了3级塔式分解示意图以及相应的频带划分示意图。在j尺度下，带通滤波器的频域区间为，低通滤波器的频域区间是经k级塔式滤波，得到k+1个子带图像。

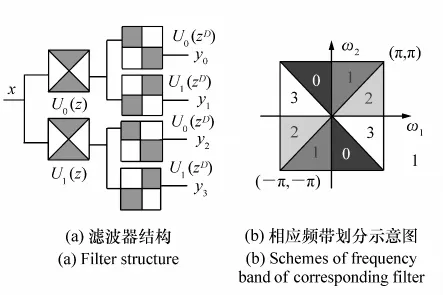
图4 采用二通道扇形滤波器实现四通道方向分解示意图Fig.4 Schematic diagram of realization of four channel direction decomposition by using two channel fan filter

NSCT采用的NSDFB也是一组二通道非下采样滤波器组，如图2(b)所示。其中，分解滤波器{U0(z)，U1(z)}和合成滤波器{V0(z)，V1(z)}也满足Bezout恒等式，从而保证了NSDFB满足重构条件。采用理想频域支撑区间为扇形的滤波器U0(z)和U1(z)可以实现二通道方向分解。例如，按采样矩阵对滤波器U0(z)和U1(z)上采样，得到U0(zD)和U1(zD)滤波器，如图4所示。如果再对子带图像进行滤波，可实现四通道的方向分解。同理采用更为复杂的采样矩阵可得到的更多方向分解［15］。尺度j下经N级分解，可得到方向分解级数lj的个子带图像。源图像经NSPFB分解后，再将带通子带图像输入到NSDFB中，即可得到图像的带通方向信息。

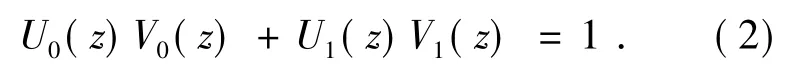
3 图像融合策略

对于融合的性能来说，除了图像的多尺度分解和重构工具，融合规则非常重要。融合规则可分为基于像素选取的融合规则、基于窗口的融合规则和基于区域的融合规则。

在图像的分解中，低频系数的融合多采用加权平均法，定义如下:

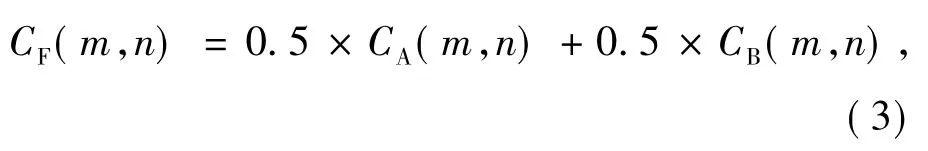
其中:A，B为源图像，F为融合图像，Ci(m，n)为图像i分解得到的低频子带在(m，n)处的系数。加权平均法将清晰区域的系数与模糊区域的系数进行“结合”，在提高模糊区域质量的同时，造成了清晰区域信息的损失，表现为融合图像的对比度下降。本文采用基于区域梯度信息的系数融合准则，原理如下:

如果CA(m，n)=0或CB(m，n)=0，则

CF(m，n)=0.5 ×CA(m，n)+0.5 ×CB(m，n)。

如果CA(m，n)≠0且CB(m，n)≠0，则

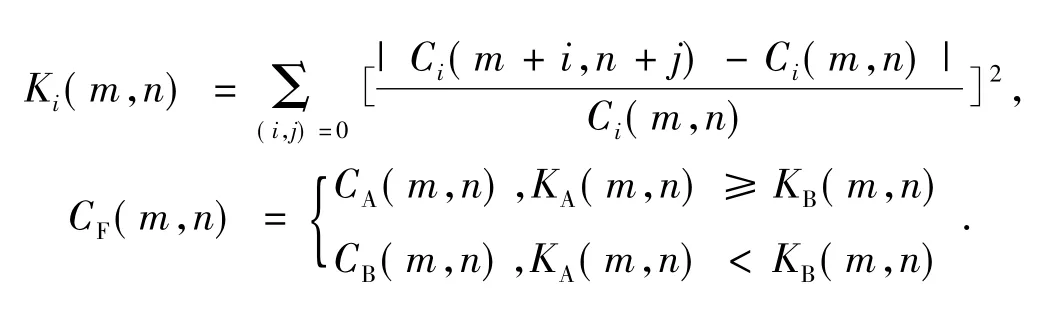
绝对值较大的高频系数对应于图像中对比度变化较大的边缘等特征，而人眼对于这些特征比较敏感。所以，对于高频系数多采用绝对值取大的融合准则，原理如下:

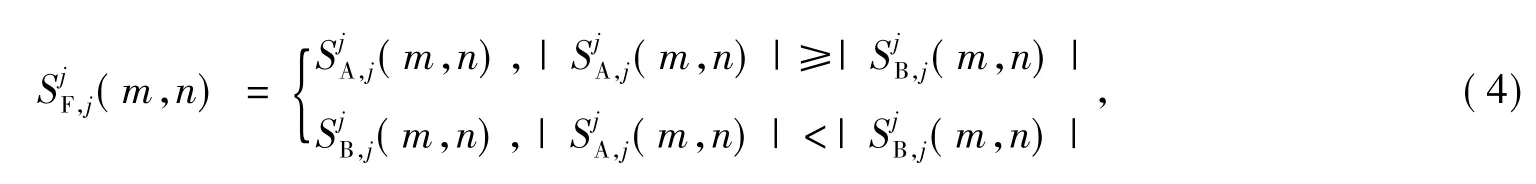
其中:j=1，2，…，N代表分解的层数;i=1，2，3 代表每一层高频系数的3个方向。

本文采用加权与选择相结合的准则。该准则考虑了两幅源图像之间的相关性，根据相关性的不同，分别采用选择和平均的算法。当两幅源图像之间的相关性较弱时，选择邻域能量较大的点;当两幅源图像之间的相关性较强时，将待融合的高频系数进行加权，原理如下:

对不同方向的高频子带可采用区域系数绝对值加权和作为区域特征因子对高频系数进行融合。定义高频子带在区域Q内的邻域能量为活性测度:

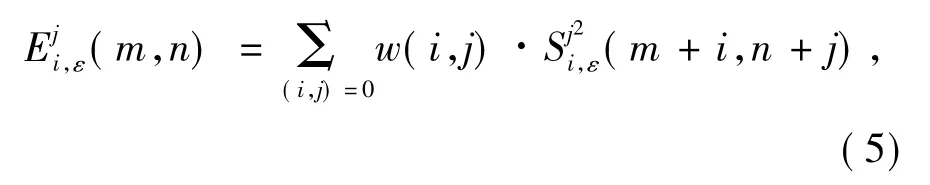
其中:j=1，2，…，N代表分解的层数;ε =1，2，3 代表每一层高频系数的3个方向;w(i，j)为权系数，满足

匹配测度为区域归一化互相关函数:

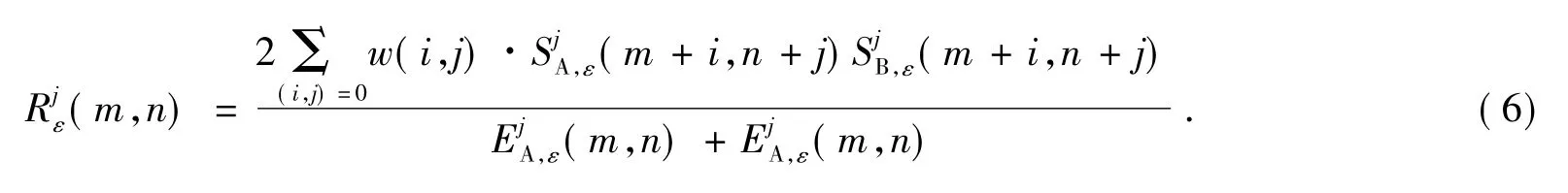
加权系数计算方法如下:

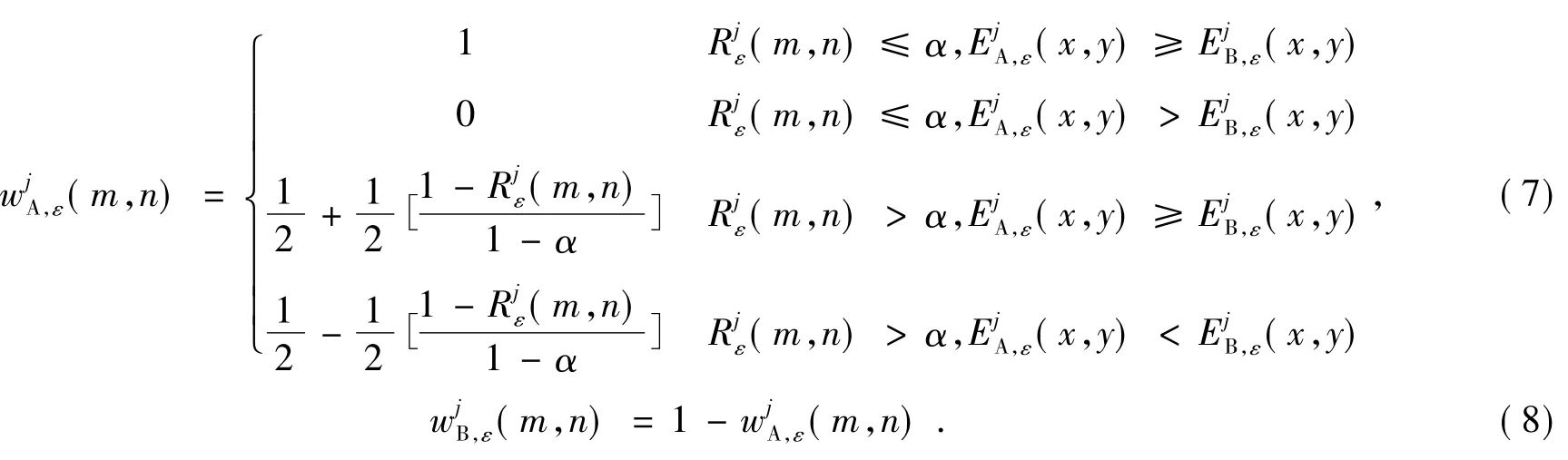
融合图像相应的高频子带表达式:

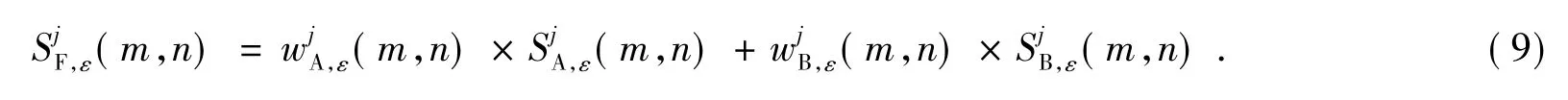
基于区域梯度信息的系数融合准则考虑了图像的边缘等特征，提高了清晰区域的低频系数选取的准确性。这种加权与选择相结合的融合准则充分考虑了源图像高频子带系数之间的相关性。

4 基于NSCT的融合试验

NSCT分解得到的高频子带的个数可以灵活控制，因此，有必要研究NSCT分解的层数和方向子带的个数对融合结果的影响。通过高频子带合成图像可以看出每一种分解情况下得到的所有的细节信息。如下列实验图像所示，随着分解层数和分解高频子带个数的增加，提取出来的细节信息不断增加;在一定范围内，高频子带个数的增加能够突出图像的边缘信息，随着高频子带的继续增加，其它的非边缘信息也会得到加强。

图5 分解层数、分解高频子带个数实验Fig.5 Experiments of decomposition of layers and decomposition of high frequency sub-band numbers

图5 中分解层数和每层的高频子带个数用［d1，d2，…dl］表示，di代表第i层高频子带的个数，i=1，2，...，L代表分解层数。当分解层数为1时，融合图像在数字的边缘处存在模糊，而当分解层数为2和3时，融合图像中模糊现象明显减弱，说明分解层数的增加能够提高算法的细节表现力。

为了验证该融合算法的有效性和正确性，采用两组红外与可见光图像进行融合实验。经过配准后的可见光与红外图像大小为256 pixel×256 pixel，如图6所示。

图6 红外与可见光图像融合实验(1)Fig.6 The first experiments of infrared and visible image fusion

验证算法的同时，还采用了其它融合算法(加权平均算法、拉普拉斯变换融合、小波变换(WT)、离散小波变换(DWT)、离散小波框架变换(DWFT)、Contourlet变换(CNT)以及NSCT等不同图像多尺度变换)进行性能比较。在所有基于多尺度分解的图像融合算法中，图像分解级数均为4级，基于NSCT融合算法中，尺度方向分解级数分别为2，3，3，4。采用平均梯度G、信息熵E以及基于图像边缘梯度信息的Q因子对融合性能进行客观评价。

从融合的结果可以看出，几种融合方法都改善了原始图像的视觉效果，丰富了图像信息，提高了图像的清晰度。相比于其它图像，图6(f)的细节信息得到了更好的保留，纹理更清晰，有效地消除了图像的模糊。

图7 红外与可见光图像融合实验(2)Fig.7 The second experiments of infrared and visible image fusion

图7 是另一组融合实验图像。从融合的结果可以看出，几种融合方法都改善了原始图像的视觉效果。相对于源图像而言，图7(c)对比度明显降低。图(d)中引入了较为明显的“虚假”信息，尤其是纹理比较丰富的部分，而在图(e)与图(f)中，“虚假”信息得到了抑制，主要原因是相对DWT算法，DWFT和NSCT算法没有采用上采样和降采样，在分解和重构的实现过程中，避免了以前引入的频率混叠项。相对于图(e)的图像，图(f)细节更加丰富，主要原因是由于NSCT相对于DWFT具备更稀疏的图像表示以及方向选择性能力，变换后的图像更加集中体现能量，有利于对图像中重要的几何特征进行更好的跟踪和捕捉。

NSCT处理后能量更加集中，提供了更多的图像信息。另外，变换的平移不变特性使其能够有效减少配准误差对融合性能的影响。图像经非下采样Contourlet分解得到具有同尺寸的各子带图像，有利于融合运算的实现，因而具有较快的运算速度，另外本研究在工程应用时对算法应用的实时性无严格要求。因此，非下采样Contourlet变换可以作为更适合图像融合的MGA工具。

5 结论

NSCT作为多尺度分解的一个重要手段，逐渐在图像融合研究领域中广泛应用。本文基于NSCT，重点针对红外图像与可见光图像的融合，提出了加权与选择结合的图像融合算法，针对低频子带系数和各带通方向子带系数提出了低频基于区域梯度信息、高频基于区域特征因子的融合方案。实验结果表明:相对于基于像素的图像融合算法，基于区域梯度信息与区域特征因子的图像融合算法具有更高的融合性能。

［1］毛士艺，赵巍.多传感器图像融合技术综述［J］.北京航空航天大学学报，2002，28(5):512-518.MAO SH Y，ZHAO W.Comments on multisensor image fusion techniques［J］.J.Beijing University Aeronautics and Astronautics，2002，28(5):512-518.(in Chinese)

［2］SIMONE G，FARINA A，MORABITO F C.Image fusion techniques for remote sensing application［J］.Information Fusion，2002，3(1):3-15.

［3］杜宝祥.Contourlet变换在图像处理中的应用研究［D］.哈尔滨：哈尔滨工程大学，2009.DU B X.Recearch on applications of contourlet transform in image processing［D］.Harbin:Harbin Engineering University，2009.(in Chinese)

［4］WEN C Y，CHEN J K.Multi-resolution image fusion technique and its application to forensic science［J］.Forensic Science International，2004，140(2-3):217-232.

［5］PAN J P，GONG J Y，LU J，et al..Image fusion based on local deviation and high-pass filtering of wavelet transform［J］.SPIE，2004，5660:191-198.

［6］TU T M，HUANG P S，HUNG C L，et al..A fast intensity-hue-saturation fusion technique with spectral adjustment for IKONOS imagery［J］.IEEE Geoscience and Remote Sensing Lett.，2004，1(4):309-312.

［7］宋好好.Contourlet变换在图像分析处理中的应用研究［D］.上海：上海交通大学，2008.SONG H H.Application research on contourlet in image processing［D］.Shanghai:Shanghai Jiaotong University，2008.(in Chinese)

［8］HEATHER J P，SMITH M I.Multimodal image registration with applications to image fusion［C］.2005 7th IEEE International Conference on Information Fusion，Philadelphia，Pa，25-28 July，2005:372-379.

［9］杨俊，赵忠明.基于Curvelet变换的多聚焦图像融合方法［J］.光电工程，2007，6(1):11-16.YANG J，ZHAO ZH M.Multifocus image fusion method based on curvelet transform［J］.Opto-Electronic Eng.，2007，6(1):11-16.(in Chinese)

［10］NIKOLOV S G，HILL P R，BULL D R，et al..Wavelets for image fusion［EB/OL］.(2001-03-06)［2011-07-21］.http://www.tallypaul.pwp.blueyonder.co.uk/papers/nikolov-wif.pdf.

［11］SHI W Z，ZHU C Q，TIAN Y，et al..Wavelet-based image fusion and quality assessment［J］.International J.Appl.Earth Observation and Geoinformation，2005，6(3):241-251.

［12］STARCK J L，CANDES E，DONOHO D L.The curvelet transform for image denoising［J］.IEEE T.Image Process.，2002:670-684.

［13］CANDES E J，DEMANET L，DONOHO D L.Fast discrete curvelet transform［EB/OL］.(2005-01-10)［2010-07-21］.http://www.acm.caltech.edu/emmanuel/paper/FDCT.pdf.

［14］倪伟.基于多尺度几何分析的图像处理技术研究［D］.西安：西安电子科技大学，2008.NI W.Research on image processing algorithms via multiscale geometric analysis［D］.Xi'an:Xi'an Univeristy of Electronic Science and Technology，2008.(in Chinese)

［15］BENDER E J，REESE C E，SVANDERWAL G.Comparison of additive image fusion vs.feature-level image fusion techniques for enhanced night driving［J］.SPIE，2003，4796:140-151.