应用加权残值法求解结构动力学问题

连 鹏

1 加权残值法

结构物中的杆件、板壳等弹性体，受到动荷载作用时，在工程设计中的动力分析问题有时候是比较突出的问题［1，2］。作用在结构物上的动荷载往往是一种突加的荷载，作用的时间往往是很短暂的，但强度很大。结构物在突加的强大而又短暂的动荷载作用下，产生过度的变形及巨大的内力以致在短暂的时间内发生破坏倒坍，这种情况称为动力响应问题。目前这类问题的计算，主要依赖有限元分析。这种方法虽然有效，但往往工作量大，浪费巨大的人力物力，在近年来国内计算力学工作者提出应用加权残值法分析结构物动力响应问题［3，4］。这种方法具有简便、精确、工作量少、经济等特点，是一种将加权残值法用于结构物动力学方面的很有意义的研究工作。

2 基本原理

以现有理论计算结构物的动力平衡微分方程，一般应用直接积分法，此法要点是利用时间为t的结构物的位移Ut，速度U＆t及加速度U＆t＆，去计算时间为t+Δt时结构物的位移Ut+τ，速度及加速度，现在所用的动力学平衡方程式为:

这个方法的基本假设认为:在时间间隔τ=θΔt之中，加速度向量作线性变化。在θ=1.37时，无条件稳定，效果尚佳。

国内孙焕纯曾有文章修改威尔逊法中的假设，缩短计算过程。金瑞春根据加权残值法的概念写出结构动力响应问题中的运动微分方程的广义积分格式，从特例推出威尔逊—θ法。徐文焕提出以B样条配点法解算结构运动微分方程式，线性的及非线性结构动力学响应问题。徐次达及其合作者研究做了大量样条配点法解算板壳动力响应问题，发展更完善的有条件及无条件稳定的动力响应问题计算格式。

徐文焕首先提出了用样条函数表达时域函数，利用配点法解决结构的动力响应问题。在他提出的配点法中，将时域［t0，tm］作均匀划分，时间步长为:

结构物的第“n”个振型坐标以三次B样条函数表示为:

配点法为i的残值方程为:

解得结构物在t=t0时“n”振型的振型位移、速度及加速度分别为:

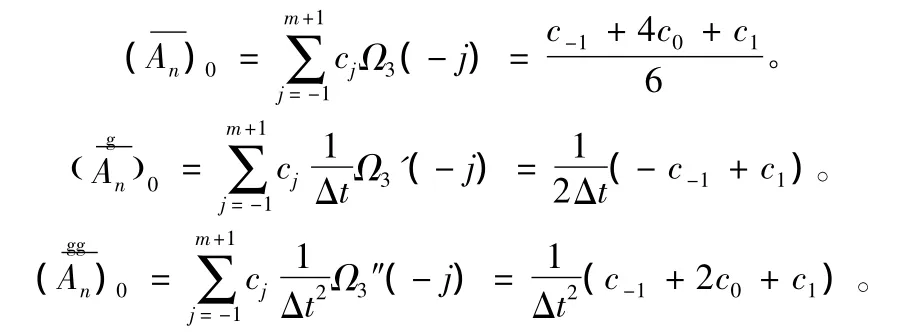
在t=ti时振型位移、速度及加速度分别为:

ti+1时刻的三个量与ti时刻的关系式如下:

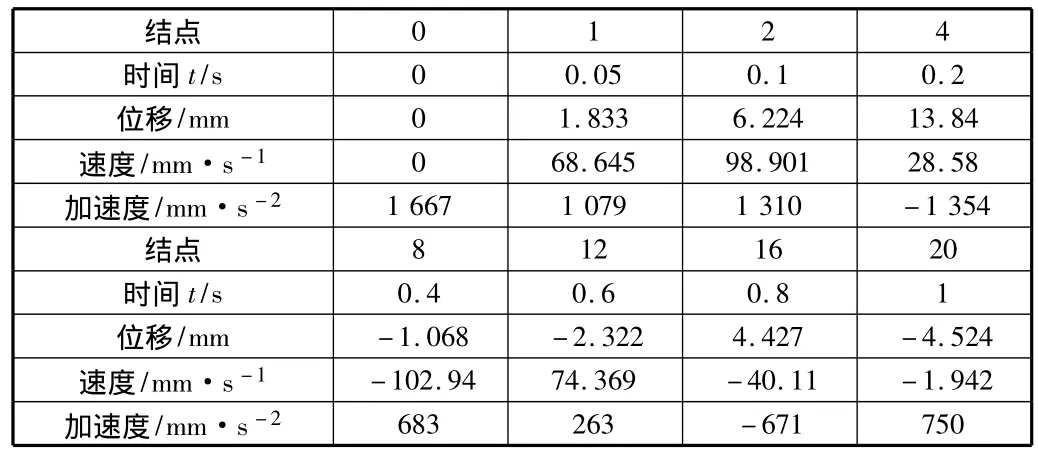
表1 配点法计算结果

表2 威尔逊法计算结果

3 求解算例

使用配点法计算结果见表1。

使用威尔逊法计算结果见表2。

通过两种方法的计算结果对比可知，使用配点法进行计算是一种节省资源，高效准确的计算方法，在适当的情况下，是可以取代有限元进行工程力学分析的。

［1］ 徐次达.计算力学中的加权残值法在我国的研究及应用［J］.力学与实践，1998(1):18-19.

［2］ 钟新谷，曾庆元.加权残值法在钢筋混凝土拱桥非线性有限元分析中的应用［J］.计算力学学报，1999(4):51-52.

［3］ 张新占，冯忠居.用加权残值法求解加筋圆柱曲板的临界载荷［J］.陕西工学院学报，2000(1):31-34.

［4］ 王光杰.滑动最小二乘法在加权残值法中的应用［J］.桂林工学院学报，2000(3):26-27.