近景摄影测量大角度外方位元素解算方法研究

冀 云

(重庆电子工程职业学院，重庆401331)

近景摄影测量大角度外方位元素解算方法研究

冀 云

(重庆电子工程职业学院，重庆401331)

为了提高大角度近景摄影测量的外方位元素解算的精度，介绍了推导包含共线方程泰勒展开二次项的非线性误差方程式，并建立其外方位元素的数值解算方法。多个工程实例表明该方法有助于提高大角度摄影的外方位元素解算的精度和求解稳定性，具有一定的应用价值。

大角度近景摄影测量；共线方程的非线性特征；外方位元素解算方法

1 引言

风洞试验是依据运动的相对性原理，将飞行器的模型或实物固定在地面人工环境中，人为制造气流流过，以此模拟各种复杂的飞行状态。

为了得到准确的试验数据，在高速风洞高速压实验条件下，需要用摄影测量技术测量试验模型的变形，以修正试验数据。因高速风洞的试验段的空间尺寸有限，相机及其照明的安装位置受限，故双（多）相机大角度大重叠的近景摄影方式不可避免。航空摄影测量是近似于垂直的摄影，可用小角度的线性化模型解得较高精度的外方位元素，即在共线方程的泰勒展开式，只取了一次小项，因旋转角很小，线化后通过方程迭代能够收敛于正确的解；而大角度大重叠的近景摄影测量，必须考虑共线方程的非线性特征才能提高外方位元素中的大旋转角度值的解算精度和求解稳定性。为此，本文推导包含共线方程泰勒展开二次项的非线性误差方程式，并提出相应的外方位元素的非线性数值解算方法。

2 共线方程的非线性误差方程式

共线方程描述了摄影中心、像点、物点三点共线这样一个严密的数学模型，表达式如下：

式中(x0,y0,f0)为内方位元素,(Xs,Ys,Zs)分别为地面点以及摄影中心在地面坐标系下的坐标,(a1,a2,a3,b1,b2,b3,c1,c2,c3)为由外方位角元素(φ,ω，k)所组成的旋转矩阵R中9个方向余弦。

鉴于共线方程的泰勒展开表达式中旋转角度的三阶偏导数为0，同时为了减少计算量，本方法只需推导至包含二次小项的共线方程的非线性误差方程式，具体如下：

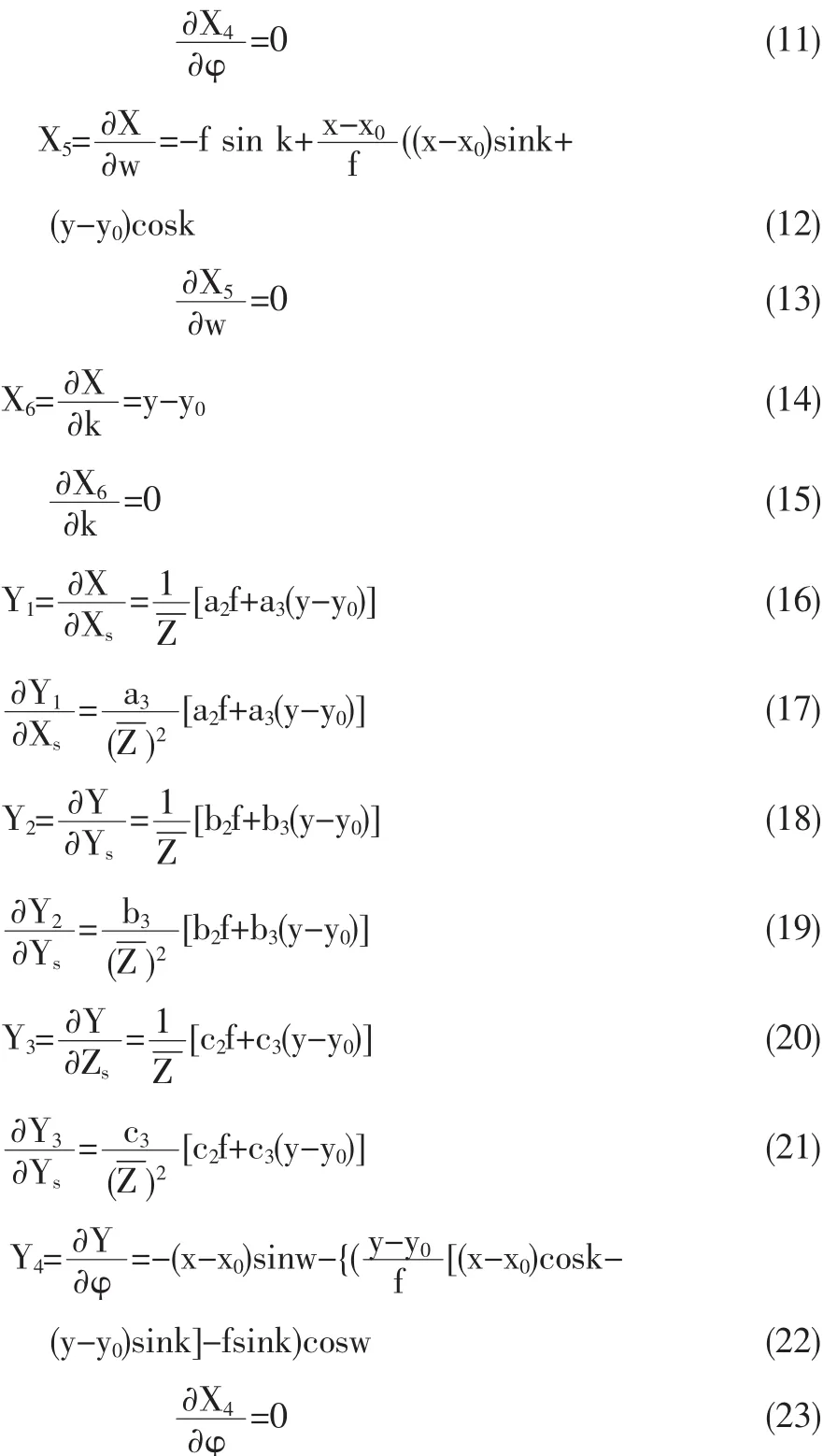
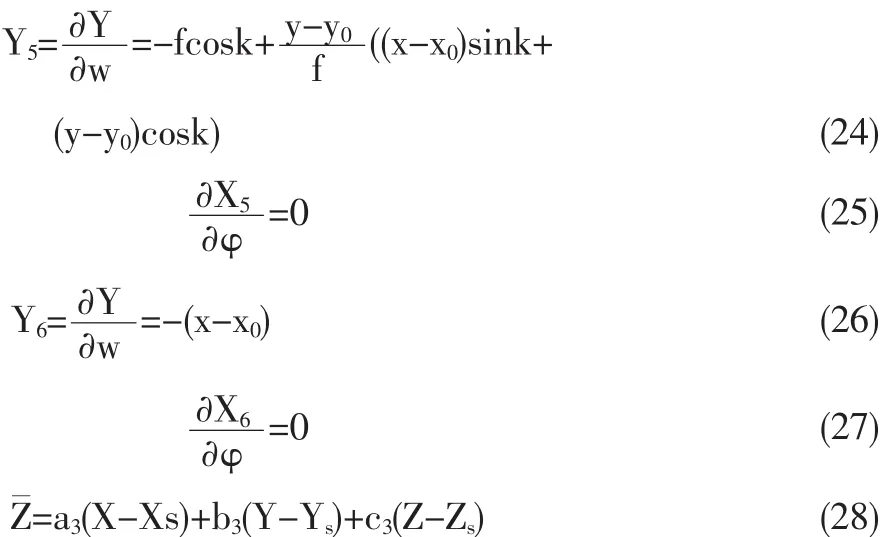
式中lx与ly分别为给定像点的x与y坐标残差，dXs,dYs,dZs,dφ,dw,dk为外方位元素近似值的修正数。为求解该修正数,至少需要3个控制点。本文采用3个控制点联解式(2)与式(3)即可得到外方位元素修正数。

3 非线性误差方程式的数值解法

常用的非线性方程的解法有拟牛顿法、对分法、梯度法、蒙特卡洛法等。蒙特卡洛法适应性强、收敛性与问题维数无关、原理及程序简单等优点,特别在大角度共线方程求解中,待求修正数往往较大，该方法能提高计算的可靠性，结果更为稳定。但蒙特卡洛法的收敛速度与一般的数值计算方法相比是较慢的，并且如果搜索域不恰当，会得到不正确的解。为此，本文提出蒙特卡洛法的搜索域对摄影角度的自适应方法，即建立搜索域大小B与外方位元素最大角度间的最佳数学模型，解决收敛速度慢与收敛精度问题。

本文对蒙特卡洛方法的搜索域进行大量的实验研究，获得的典型数据列举如表1所示:

表1 搜索域B与最大角x的关系

采用美国商用统计分析软件SPSS（statisticspackage for social science)11.5对搜索域B与外方位元素最大角度进行非线性回归分析。如图1所示，较粗曲线为观察曲线，根据观察曲线的形态，选择Quadratic函数拟合得到B=256.433x2-35.932x+2.4369(29)。

式（29）即为蒙特卡洛法的搜索域B与外方位元素最大角度间的映射模型，图1中较细曲线为式（29）的均方逼近曲线。按照角锥法求解外方位元素的初值，按照式(29)即可得到搜索域B，最后利用蒙特卡洛算法联立求解式(2)与式(3)得到外方位元素的值。

4 实验验证与精度分析

本文提出的算法已采用Microsoft Visual Studio 2005的C#语言程序验证，文中表2与表3的数据都来源于Nikon D700数码相机（分辨率4000×3000）实际采集的图像。由于篇幅所限，本文仅给出表2与表3中的外方位角度最大的2幅照片(如图2所示)。

图1 外方位元素最大角度与搜索域B的关系图

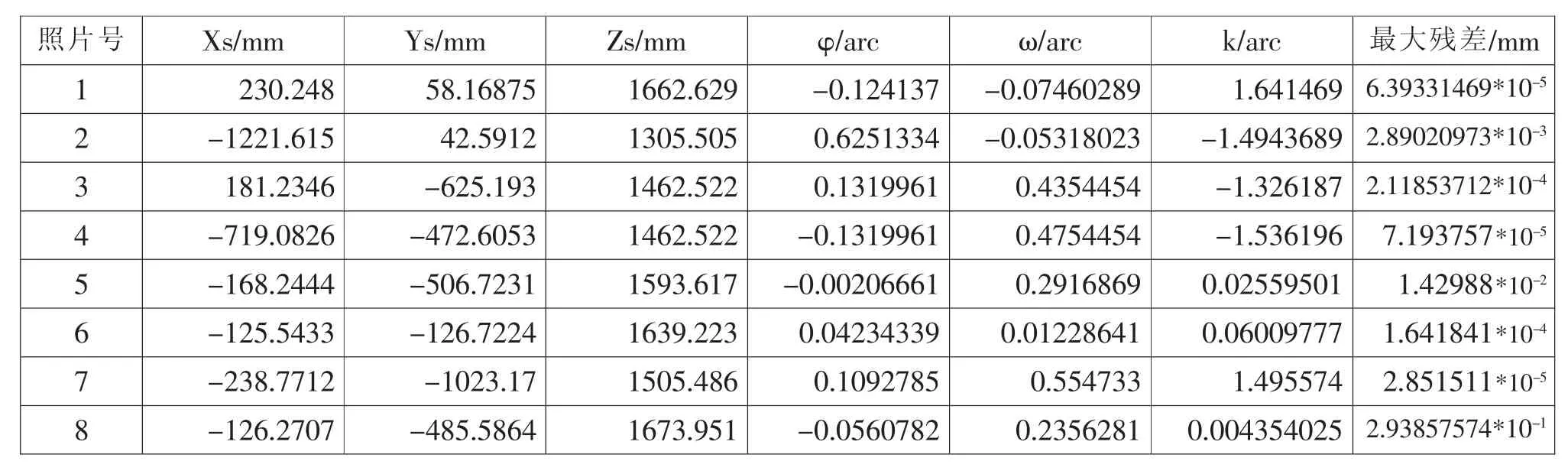
表表22 共共 线线 方方 程程 的的 传传 统统 线线 化化 误误 差差 方方 程程 求求 解解 相相 关关 数 据 表

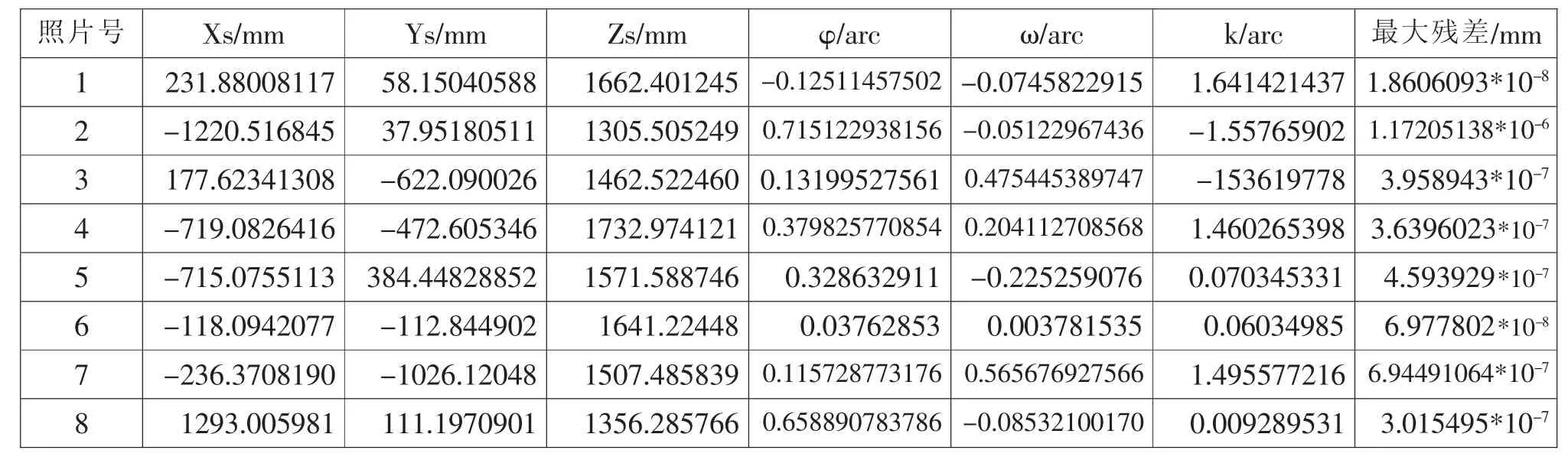
表3 本文算法相关数据表

图2 表2与3中的外方位角度最大的2幅照片

对每张照片给定3个相同的控制点求解外方位元素，采用共线方程的传统线化误差方程求解的像点残差如表2所示，采用本文算法得到的像点最大残差如表3所示。对比表明,本文算法计算得到的外方位元素值精度更高（最大残差至少降低3个数量级)，尤其是在大角度情况下也能稳定得到较高精度的外方位元素 （如表2、3中照片号为8的照片的像点最大残差甚至从10-1降到10-7），从而确保前方交会得到高精度的待求点坐标。因此证明了本文讨论算法的正确性和稳定性。

5 结论

本文推导了包含共线方程泰勒展开二次项的非线性误差方程式，并提出其外方位元素的数值解算方法，多个工程实例表明本文方法提高了大角度摄影的外方位元素解算的精度和求解稳定性 （与共线方程的传统线化误差方程求解相比），具有一定的应用价值。

[1]冯文灏.近景摄影测量—物体外形与运动状态的摄影法测定[M].武汉:武汉大学出版社,2002.1-14

[2]Danny A Barrows.Videogrammetric Model Deformation Measurement Technique for Wind Tunnel Applications,45th AIAAAerospace SciencesMeeting and Exhibit,8-11 Jan.2007,Reno,NV,United States,AIAA Paper 2007-1163

[3]陈义,陆珏,郑波.近景摄影测量中大角度问题的探讨[J].测绘学报，2008，(11).

TP39

A

1674－5787（2011）03－0157－03

2011-03-20

冀云，男，重庆电子工程职业学院电子信息系，助理工程师。

责任编辑 王荣辉